ЛАБ 3-4 2011. петербургский государственный университет путей сообщения
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
|
Таблица измерений и вычислений
 Указания по построению векторных диаграмм Построение векторных диаграмм для всех пунктов программы лабораторной работы начинается с построения симметричной трехлучевой звезды векторов фазных напряжений генератора Такая векторная диаграмма генератора сохраняется для всех пунктов настоящей работы. Если ее дополнить векторной диаграммой фазных напряжений приемника (в том числе при обрыве нейтрального провода и несимметричном приемнике), то ее можно назвать «топографической». Векторные диаграммы принято называть топографическими, если электрические потенциалы точек на диаграмме имеют те же буквенные обозначения, что и на соответствующих точках в схеме четырехпроводной звезды (рис. 4 и рис. 10а). Покажем порядок построения такой топографической векторной диаграммы для случая симметричной нагрузки при наличии нейтрального провода (рубильник Р2 на схеме рисунка 10б замкнут). В 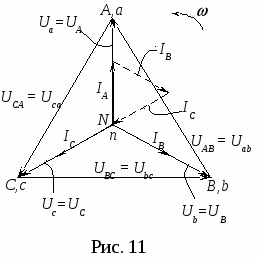 начале строится звезда векторов фазных напряжений генератора начале строится звезда векторов фазных напряжений генератора При наличии нейтрального провода, когда нейтральная точка n приемника совпадает с точкой N, фазные напряжения приемника и генератора равны друг другу Полученная векторная диаграмма фазных напряжений приемника При симметричной нагрузке (по определению) фазные (линейные) токи IЛ равны друг другу по величине IA = IB = IC и сдвинуты по фазе относительно «своих» фазных напряжений Ua, Ub, Uc на один и тот же угол φ = 0, так как в фазах приемника включены резисторы (активная нагрузка). Задавшись масштабом для токов (рекомендуется 1 см = 0,25 А), строят векторы токов и проводят их графическое сложение (рис. 11) для определения вектора в нейтральном проводе Поскольку показания приборов в схеме (рис. 10б) при выполнении второй части рассматриваемого режима (при разомкнутом рубильнике Р2) полностью идентичны с первой частью, необходимость построения второй такой же диаграммы отпадает. Векторная диаграмма при симметричной нагрузке, показанная на рисунке 11, справедлива как для случая с нейтральным проводом, так и без него. При построении топографической диаграммы для других предусмотренных программой лабораторной работы пунктов можно не показывать в вершинах треугольника линейных напряжений начала фаз приемника a, b, c, поскольку их потенциалы всегда совпадают с потенциалами начал фаз генератора (питающей сети) A, B, C. Векторные диаграммы напряжений и токов, соответствующие разгрузке одной фазы (a–x) приемника при наличии и обрыве нейтрального провода представлены на рисунках 12а и 12б соответственно. При обрыве фазы a–x (ключ Ка в схеме на рисунке 10б разомкнут) и замкнутом нейтральном проводе, ток IA = 0. Токи IB и IC остаются равными по величине и совпадают по фазе с напряжениями Ub и Uc (рис. 12а). Ток в нейтральном проводе определяется в соответствии с первым законом Кирхгофа: 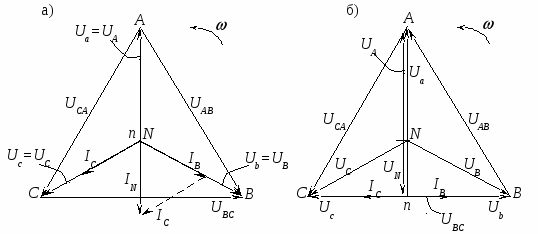 Рис. 12 Из точки n в вершины треугольника АВС проводятся фазные напряжения приемника Векторные диаграммы напряжений и токов, соответствующие разгрузке двух фаз (a–x и b–y) приемника при наличии нейтрального провода и без него представлены на рисунках 13а и 13б соответственно. При обрыве двух фаз (ключи Ка и Кb в схеме на рисунке 10б разомкнуты) и наличии нейтрального провода (Р2 замкнут) IA = 0 и IB = 0, и существует замкнутая цепь одной фазыc–z, ток которой IC равен току нейтрального провода IC = IN, фазы a–x и b–y, а также линейные провода A–a, B–b (рис. 10б) обесточены. Векторная диаграмма для этого случая имеет вид, показанный на рисунке 13а. При обрыве двух фаз и нейтрального провода (рубильник Р2 на схеме рисунка 10б разомкнут) цепь оказывается разомкнутой, и все участки цепи обесточены (IA = IB = IC = 0), за исключением высокоомных цепей вольтметров, токами в которых всегда пренебрегают ввиду их малости. Векторная диаграмма для этого режима показана на рисунке 13б. Токи на диаграмме отсутствуют; по результатам измерений показаны три вектора напряжения 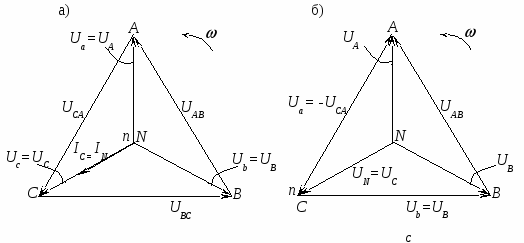 Рис. 13 Векторные диаграммы для общего случая несимметричной нагрузки, когда по трем фазам приемника протекают разные по величине токи IA IB IC, показаны на рисунках 14а и 14б. Как и в предыдущих случаях вначале строятся векторные диаграммы напряжений генератора в виде симметричной звезды и правильного треугольника (рис. 6). Векторная диаграмма при наличии нейтрального проводапоказана на рисунке 14а, где векторы токов 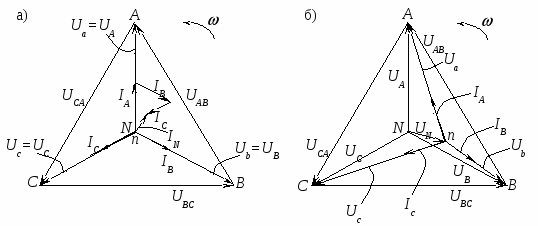 Рис. 14 Расчетные формулы для заполнения раздела таблицы измерений и вычислений (табл. 1) «Вычисления». Поскольку все режимы исследуются применительно к активному приемнику (все фазы приемника резисторы), то следует рассчитать активные мощности приемника по результатам измерения фазных токов и напряжений с учетом того, что угол φa=φb=φc=φ= 0 и cosφ = 1. Активные мощности приемника: Активная мощность всей цепи равна сумме активных мощностей отдельных фаз и вычисляется по формуле: При симметричной нагрузке активная мощность вычисляется по формуле: Полученные расчетом данные рекомендуется сравнить с результатами измерений ваттметрами. Контрольные вопросы
2.2. Лабораторная работа. Исследование приемника, соединенного треугольником Программа работы Исследовать соединение приемников при:
Схема лабораторной установки На рисунке 15 показана схема, в которую включены шесть амперметров, два ваттметра и показан переносный вольтметр V, позволяющий измерять напряжения на входных зажимах фаз приемника a, b, c. В качестве фаз приемника zab, zbc, zca используются проволочные резисторы, представляющие для генератора (питающей сети) активную нагрузку. Также на схеме показан конденсатор xc с регулируемой емкостью для выполнения пункта 6 программы работы. Амперметры Аab, Аbc, Аca (рис. 15), измеряющие фазные токи приемника, должны быть выбраны на один предел измерения (например, 2,5 А), а линейные амперметры АА, АВ, АС – на другой, более высокий предел (например, 5 А), поскольку линейные токи по величине как правило больше фазных. Ваттметры W1 и W2 включены по так называемой «схеме двух ваттметров», применяемой для измерения активной мощности в трехпроводных трехфазных цепях. Можно показать, что алгебраическая сумма PW1 PW2 показаний двух ваттметров равна сумме активных мощностей всех трех фаз. Применительно к приемнику, соединенному треугольником, можно записать: 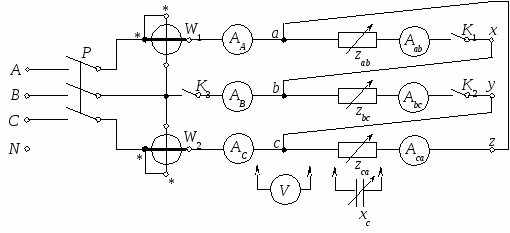 Рис. 15 Недостатком этого метода является отсутствие информации, как суммарная мощность распределяется по трем фазам приемника (за исключением случая симметричной нагрузки). Следует обратить внимание на схему включения ваттметров. Токовые обмотки ваттметров включаются в два любых линейных провода (например, А и С, как показано на рисунке 15), обмотки напряжения своими началами («звездочки») соединяются со «звездочками» токовых обмоток, а концами подключаются к «свободному» линейному проводу (B–b). Выключатели К1 и К2 (рис. 15) предназначены для размыкания фаз соответственно a–xиb–y, а выключатель К3 предусмотрен для выполнения пункта 4 программы лабораторной работы (разрыв линейного провода B–b). Трехполюсный рубильник (автомат) Р, расположенный на лабораторном щитке, позволяет включить и выключить напряжение питающей сети, подаваемое на вход схемы лабораторной установки (рис. 15). Порядок выполнения работы Перед сборкой схемы рекомендуется расположить измерительные приборы и приемники (резисторы) на рабочем месте в соответствии с тем, как это указано на схеме (рис. 15). Собирать схему удобнее отдельными блоками. Например, вначале собрать часть схемы от клемм А, В, С на щитке, включая ваттметры, ключ К3 и линейные амперметры АА, АВ, АС, не подключая их к началам a, b, c приемника. Затем отдельно собрать схему (рис. 15) треугольника (выключатели К1 и К2 вмонтированы в проволочные резисторы, которые являются фазами приемника). После этого можно закончить сборку схемы, подключив линейные амперметры к началам фаз приемника. После проверки правильности сборки схемы преподавателем или старшим лаборантом разрешается включить напряжение рубильником (автоматом) Р (рис. 15). Работа выполняется в порядке, указанном в программе. Вначале устанавливается симметричный режим работы приемника. При включенных выключателях К1, К2, К3 и рубильнике Р (рис. 15) устанавливают одинаковые по величине токи в фазах Iab, Ibc, Ica, регулируя сопротивление резисторов и наблюдая за показаниями амперметров Аab, Аbc, Аca. Поскольку во всех фазах включены резисторы (активная нагрузка) и токи в фазах совпадают по фазе со «своими» фазными напряжениями, то нагрузка будет симметричной. Снимают показания всех приборов и заносят результаты измерения в первую строку таблицы измерений и вычислений (табл.2). Фазные напряжения измеряются переносным вольтметром V (рис. 15), который поочередно подключается к парам клемм a, b, c приемника или линейных амперметров АА, АВ, АС. Проделанная настройка резисторов на симметричный режим сохраняется и при выполнении пунктов 2,3 и 4 программы работы. Обрыв (разгрузка) фаз производится выключателями К1 и К2 (пункты 2 и 3 программы). Обрыв линейного провода осуществляется выключателем К3 при замкнутых ключах К1 и К2 (пункт 4 программы). Несимметричная нагрузка в общем случае (пункт 5 программы) создается различными сопротивлениями резисторов в фазах приемника. Изменяя сопротивления резисторов (при замкнутых выключателях К1, К2, К3), добиваются разницы в фазных токах не менее 0,5 А. Равномерная нагрузка – это частный случай несимметричной нагрузки, при которой величины токов в фазах равны, а углы сдвига по фазе между токами и «своими» фазными напряжениями различны. Такой режим (пункт 6 программы) достигается заменой резистора в фазе с–а конденсатором (рис. 15) с сопротивлением хс, в результате чего углы сдвига в фазах приемника будут разными: φab = 0, φbc = 0, φca = –π/2, то есть вектор тока Равенство величин токов в фазах достигается совместным регулированием сопротивлений резисторов и емкости батареи конденсаторов, то есть добиваются равенства r1 = r2 = xc, где r1 и r2 – сопротивления резисторов в фазах a–xиb–y, а xc – емкостное сопротивление в фазе с–z. Результаты измерений для всех шести пунктов программы заносятся в соответствующие строки таблицы измерений и вычислений (табл.2). Содержание отчета
Указания по построению векторных диаграмм Построение векторных диаграмм для всех пунктов программы лабораторной работы начинается с построения с соблюдением масштаба напряжений (1 см = 20 В) симметричной трехлучевой звезды векторов фазных напряжений приемника, соединенного треугольником, которые одновременно являются линейными напряжениями генератора (питающей трехпроводной сети): Вначале рассмотрим построение векторной диаграммы напряжений и токов для случая симметричной нагрузки (рис. 16). П 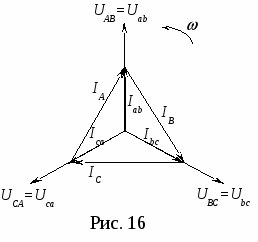 оскольку симметричный режим характеризуется равенством величин фазных токов Iab = Ibc = Ica = IФ и равенством углов сдвига φab = φbc = φca = 0 (активная нагрузка – резисторы), то задавшись масштабом тока (1 см = 0,25 А), можно определить длину IФ векторов фазных токов и построить их совпадающими со «своими» фазными напряжениями (рис. 16). Ранее было показано (рис. 8), что векторы линейных токов оскольку симметричный режим характеризуется равенством величин фазных токов Iab = Ibc = Ica = IФ и равенством углов сдвига φab = φbc = φca = 0 (активная нагрузка – резисторы), то задавшись масштабом тока (1 см = 0,25 А), можно определить длину IФ векторов фазных токов и построить их совпадающими со «своими» фазными напряжениями (рис. 16). Ранее было показано (рис. 8), что векторы линейных токов Так как режим симметричный, то векторы фазных токов В 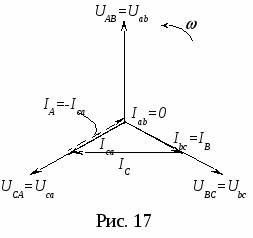 екторная диаграмма при обрыве одной фазы строится в том же порядке: изображается симметричная звезда векторов фазных напряжений, а затем строятся векторы фазных токов екторная диаграмма при обрыве одной фазы строится в том же порядке: изображается симметричная звезда векторов фазных напряжений, а затем строятся векторы фазных токов 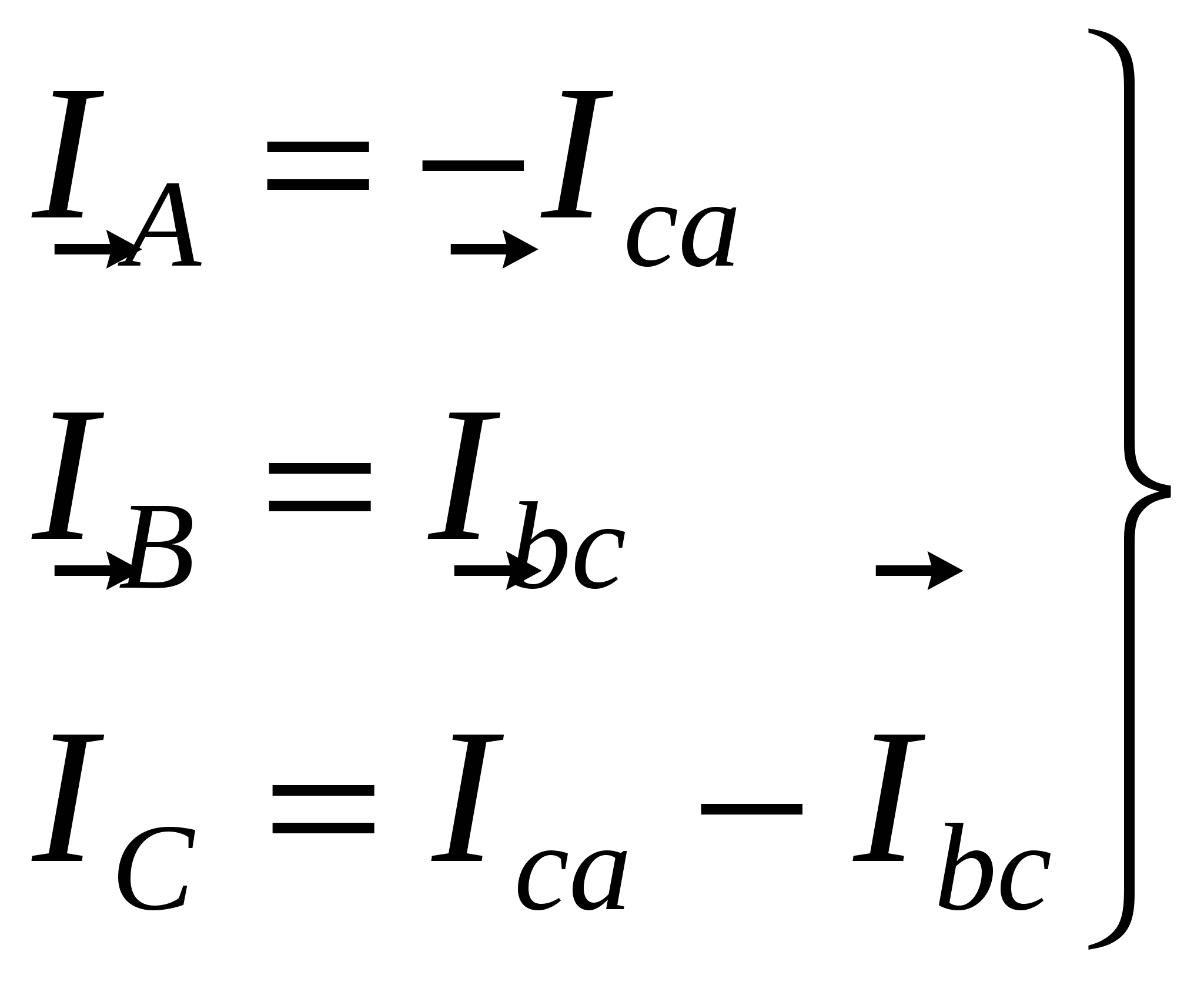 Таблица 2 Таблица измерений и вычислений
 В 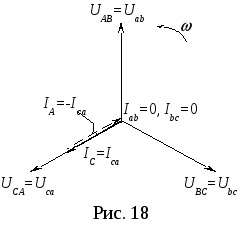 екторная диаграмма при обрыве двух фаз (рис.18) строится с учетом того, что Iab = 0, Ibc = 0 и остается неизменным ток Iса в фазе с–а. Сделав соответствующие уточнения в системе уравнений для линейных токов (6), получим: екторная диаграмма при обрыве двух фаз (рис.18) строится с учетом того, что Iab = 0, Ibc = 0 и остается неизменным ток Iса в фазе с–а. Сделав соответствующие уточнения в системе уравнений для линейных токов (6), получим: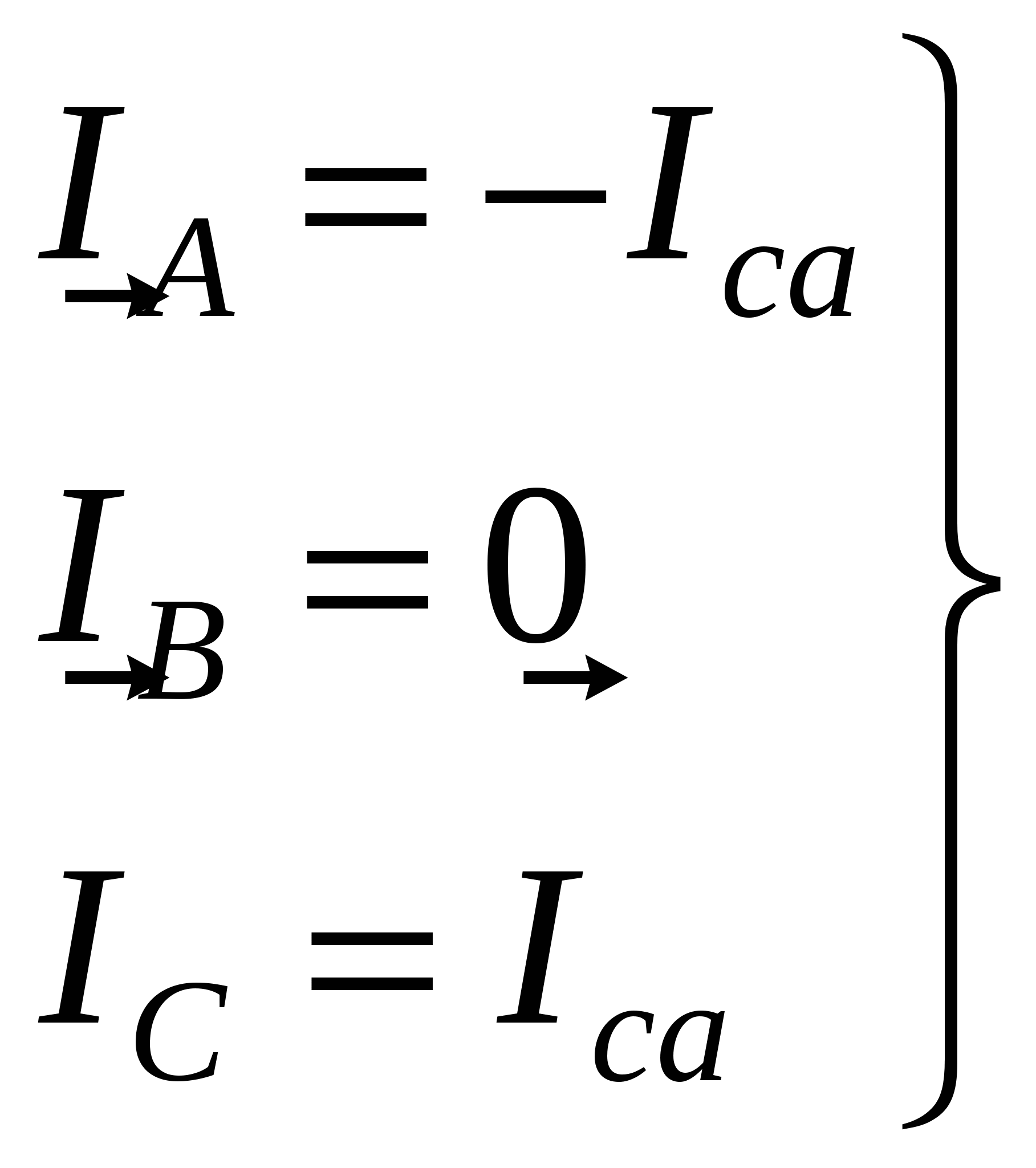 Таким образом один линейный ток IВ равен нулю, а два других равны по величине фазному току оставшейся включенной фазе с–а. В рассмотренных режимах разгрузки одной и двух фаз приемника наглядно проявляется независимость работы фаз треугольника. В 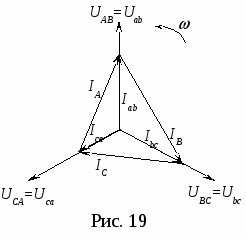 екторная диаграмма при несимметричной нагрузке всех трех фаз приемника (рис. 19). Порядок построения, как и в предыдущих режимах, сохраняется: вначале строится симметричная звезда векторов фазных напряжений екторная диаграмма при несимметричной нагрузке всех трех фаз приемника (рис. 19). Порядок построения, как и в предыдущих режимах, сохраняется: вначале строится симметричная звезда векторов фазных напряжений Векторная диаграмма при равномерной нагрузке отличается от предыдущих тем, что в одной из фаз приемника (фазе с–z) векторы тока и напряжения не совпадают друг с другом, а ток Ica опережает напряжение на 90° (φca = –90°). Это объясняется тем, что в фазу с–z вместо резисторов включен реактивный элемент – конденсатор с емкостью С (рис. 15). Построение диаграммы начинается с изображения звезды векторов фазных напряжений (рис. 20). Затем строятся одинаковые по длине векторы фазных токов: в фазах a–x и b–y совпадающими со своими фазными напряжениями, а вектор тока Н 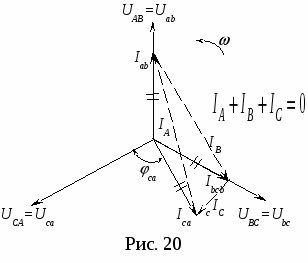 есимметричной оказывается и система трех векторов линейных токов есимметричной оказывается и система трех векторов линейных токов Это свидетельствует о том, что равномерная нагрузка при одинаковых величинах фазных токов является частным случаем несимметричной. Следует обратить внимание (рис. 20), что один из линейных токов IC меньше фазного (при симметричной нагрузке Векторная диаграмма при обрыве линейного провода B–b представляет собой векторную диаграмму однофазной цепи (рис. 21б). Данный режим осуществляется размыканием выключателя К3 (схема на рис. 15) при замкнутых ключах К1 и К2, причем до этого приемник, соединенный треугольником, представлял собой симметричную активную нагрузку: rab = rbc = rca = r , где r – активное сопротивление одной фазы. 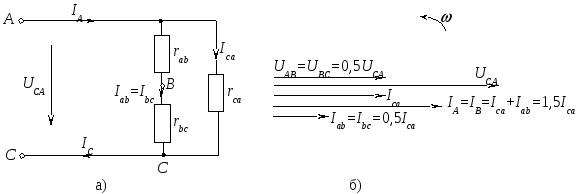 Рис. 21 Получилась по существу уже не трехфазная, а однофазная цепь с двумя параллельными ветвями (рис. 21а), включенная на однофазное напряжение UCA (соответствующее линейное напряжение трехфазного источника питания). Поэтому она должна рассчитываться и анализироваться с использованием методов расчета однофазных цепей. Активные сопротивления двух параллельных ветвей, включенных между электрическими узлами A и С однофазной цепи (рис. 21а) соответственно равны rab + rbc = 2r и rca = r . Токи в параллельных ветвях: Поскольку в рассматриваемой однофазной цепи включены только резисторы, то векторы напряжений и токов на всех участках цепи совпадает по фазе. На рисунке 21б показаны векторные диаграммы для всех ветвей, построенные с учетом соответствующих масштабов и полученных выше соотношений для напряжений и токов однофазной цепи. Расчетные формулы для заполнения раздела таблицы измерений и вычислений (табл. 2) «Вычисления». Активные мощности фаз: Суммарная активная мощность цепи: при чисто активной нагрузке φab = φbc = φca = 0 (cos0 = 1). Реактивная мощность каждой фазы вычисляется по формуле: а полная (кажущаяся) мощность Контрольные вопросы
Библиографический список
Содержание
Учебное издание исследование трехфазных цепей переменного тока Методические указания к лабораторным работамСоставители: Рудаков Борис Владимирович,Филимонов Аркадий ГригорьевичРедактор и корректор Компьютерная верстка Н.А. Ведерникова План 2011г., № 142Подписано в печать с оригинал-макета Формат 6084 1/16. Бумага для множ.апп. Печать офсетная. Усл.печ.л. 2,0. Тираж 1000 экз. ЗаказПетербургский государственный университет путей сообщения 190031, СПб., Московский пр., 9. Типография ПГУПС. 190031, СПб., Московский пр., 9. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
