ЛАБ 3-4 2011. петербургский государственный университет путей сообщения

• Название: петербургский государственный университет путей сообщения
• Анкор: ЛАБ 3-4 2011.doc
• Дата: 16.05.2018
• Размер: 0.89 Mb.
• Имя файла: ЛАБ 3-4 2011.doc
• Тип: Документы; #19319
• страница: 1 из 3

Федеральное агентство железнодорожного транспорта

Федеральное государственное образовательное учреждение

высшего профессионального образования

«ПЕТЕРБУРГСКИЙ

ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»

Кафедра «Электромеханические комплексы и системы»

исследование трехфазных цепей переменного тока
Методические указания к лабораторным работам

Санкт-Петербург

2011

Настоящие методические указания предназначены для студентов неэлектротехнических специальностей, изучающих дисциплину «Электротехника и электроника». В указания включены две лабораторные работы: «Исследование трехфазной цепи при соединении приемника звездой» и «Исследование трехфазной цепи при соединении приемника треугольником».

Отдельно выделен раздел «Краткие сведения из теории», ознакомление с которым позволит студентам более качественно подготовиться к выполнению лабораторных работ, в частности, если необходимый материал еще не был прочитан на лекциях. Значительное внимание уделено методике построения векторных диаграмм, являющихся графической частью отчетов по выполненным лабораторным работам.

При оформлении отчетов необходимо соблюдать требования стандартов при изображении электрических схем и пользоваться чертежным инструментом.

1. Краткие сведения из теории

1.1. Основные определения

Трехфазной цепью называется совокупность трех однофазных цепей А, В, С, в которых действует симметричная система электродвижущих сил (э.д.с.).

Симметричной называется система трех синусоидальных э.д.с. одинаковой частоты f и амплитуды E_m, сдвинутых по фазе на одну треть временного периода Т.

Векторная диаграмма для амплитудных значений э.д.с. в этом случае представляет собой симметричную трехлучевую звезду векторов. На рисунке 1а представлена такая диаграмма для момента времени t = 0 с учетом того, что начальная фаза синусоиды э.д.с. фазы А равна нулю: e_A = E_mAsinωt.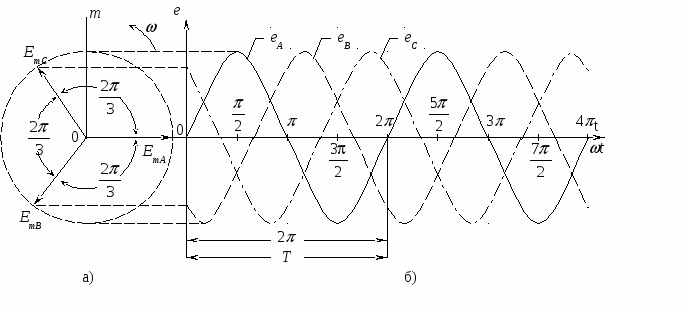



Рис. 1

Если вращать векторы диаграммы (рис. 1а) против часовой стрелки, проектируя их на вертикальную ось мгновенных значений «0m» с одновременной разверткой по горизонтальной оси, то получатся графики трех синусоидальных э.д.с. (рис. 1б), построенных в функции времени t и фазового угла t ( ==2f;  – угловая частота). Поскольку E_mA = E_mB = E_mC = E_m, то мгновенные значения э.д.с. е отдельных фаз записывается в виде: e_A=E_msint; e_B =E_msin; e_C =E_msin.

Можно показать, что алгебраическая сумма мгновенных э.д.с. (рис. 1б) и геометрическая сумма векторов, изображающих эти э.д.с. (рис. 1а), равны нулю: e_A + e_B + e_C = 0 и .

Рассмотрим устройство и принцип действия простейшего генератора трехфазного тока, поперечный разрез которого показан на рисунке 2.

На неподвижном статоре, представляющем собой пустотелый цилиндр, набранный из листовой электротехнической стали, расположены три витка А–Х, B–Y, C–Z, стороны каждого из которых находятся в двух диаметрально противоположных канавках (пазах). Магнитные оси этих витков сдвинуты относительно друг друга на одну треть пространственного периода (в показанном на рис. 3 двухполюсном генераторе – на 120 геометрических градусов).

Внутри статора вращается с постоянной угловой скоростью ω ротор, представляющий собой электромагнит постоянного тока N–S.

Т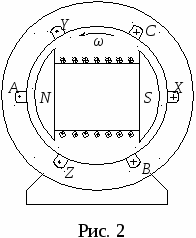ри витка (рис. 2) A–X, B–Y, C–Z, расположенные на статоре, представляют собой три генератора однофазного синусоидального тока, каждый из которых в принципе может быть подключен двумя проводами к «своему» однофазному приемнику. В этом случае получается шестипроводная, электрически разобщенная трехфазная цепь.

На практике применяются электрически связанные трехфазные цепи, соединенные звездой или треугольником. Генератор и приемник могут быть соединены в трехфазной цепи одинаково, или один из них соединен звездой, а другой – треугольником.

При вращении ротора (рис. 2) его магнитная ось N–S поочередно набегает на начала витков А, В, С, в результате чего амплитуды индуктированных э.д.с. E_mA, E_mB, E_mC (рис. 1а, б) будут сдвинуты по фазе на треть временного периода Т (на угол радиан).

Три витка A–X, B–Y, C–Z (рис. 2) на статоре простейшего генератора называются фазами генератора. Начала фаз генератора обозначаются большими буквами A, B,C, а концы фаз – большими буквами X, Y,Z латинского алфавита. Соответственно зажимы фаз приемника обозначаются малыми буквами (a–x, b–y, c–z).

За положительные направления напряжений (э.д.с.) и токов в фазах генератора принимаются направления от конца фазы к ее началу, а в фазах приемника – от начала к концу фазы.

При анализе трехфазных цепей принято считать генератор источником бесконечно большой мощности, у которого равны нулю внутренние сопротивления фаз, что позволяет э.д.с. генератора заменить соответствующими напряжениями: E_mA = U_mA, E_mB = U_mB, E_mC = U_mC. В дальнейшем вместо амплитуд синусоид будут использованы действующие (средние квадратичные за период) значения э.д.с., напряжений и токов . Это связано с тем, что реально вольтметры и амперметры в цепях синусоидального тока измеряют действующие значения соответствующих синусоидальных величин.

1.2. Трехфазная цепь, соединенная звездой

На рисунке 3 показана шестипроводная трехфазная цепь как совокупность трех самостоятельных, электрически не связанных однофазных цепей, подготовленных к соединению звездой.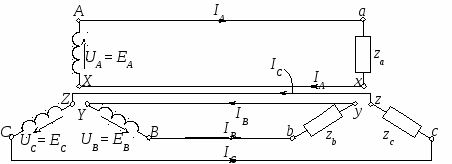



Рис. 3

Фазы генератора показаны как катушки индуктивности, буквами z_a, z_b и z_c обозначены полные (кажущиеся) сопротивления фаз приемника.

Если объединить концы фаз генератора X, Y, Z в электрический узел N, концы фаз приемника в узел n и заменить три обратных провода X–x, Y–y и Z–z одним проводом N–n, то получится электрически связанная трехфазная цепь, получившая название «звезда с нейтральным проводом». Такая схема показана на рисунке 4. Электрический узел N получил название нейтральная точка генератора, узел n – нейтральная точка приемника.

Провод N–n, соединяющий эти нейтральные точки называются нейтральным проводом.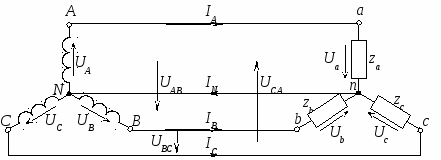



Рис. 4

Провода A–a, B–b, C–c, соединяющие начала фаз генератора с началами одноименных фаз приемника называются линейными проводами.

Фазным токомгенератора(или приемника)называется ток в фазегенератора (или приемника).

Линейным током называется ток в линейном проводе.

Фазным напряжением генератора (или приемника) называется напряжение (разность электрических потенциалов) между началом и концом одной и той же фазы генератора (или приемника).

Линейным напряжением называется напряжение между началами двух разных фаз генератора (или приемника).

Приведенные определения справедливы также и для схемы включения трехфазной цепи треугольником.

Применительно к генератору, соединенному звездой, фазное напряжениеU_A – это напряжение (разность потенциалов) между началом фазыAи ее концомX (рис. 3), или между началом фазыAи нейтральной точкойN (рис. 4), потенциал которой является электрическим потенциалом всех трех концов фаз генератора X, Y,Z.

Соотношения между фазными и линейными величинами

в схеме, соединенной звездой

Из самого принципа соединения звездой, является очевидным, что линейный ток равен фазному: I_Л = I_Ф.

Вектор тока в нейтральном проводе в соответствии с первым законом Кирхгофа равен геометрической сумме векторов фазных (линейных) токов: .

На рисунке 5 показана схема соединения фаз генератора звездой, на которой к началам двух разных фаз А и В подключен вольтметр V. Очевидно падение напряжения на внутренней цепи вольтметра будет представлять собой линейное напряжение U_AB.

При заданном (рис. 5) направлении обхода контура, образованного вольтметром V и фазами А и В генератора, можно составить векторное уравнение по второму закону Кирхгофа: . Переключив вольтметр на две другие пары зажимов, получим аналогичные равенства: , , то есть при соединении фаз генератора (или приемника) звездой вектор линейного напряжения равен геометрической разности двух соответствующих векторов фазных напряжений.

Решив полученные выше уравнения графически, можно показать, что векторы линейных напряжений образуют симметричную звезду векторов, которая опережает звезду фазных напряжений на 30°. Векторы линейных напряжений можно представить также в виде сторон равностороннего (правильного) треугольника, вершинами являются концы векторов фазных напряжений.

На рисунке 6 такая диаграмма представлена в комплексной плоскости, причем вектор фазного напряжения совмещен с положительной полуосью +1 вещественных величин.

Согласно диаграмме на рис. 6 и с учетом того, что U_A = U_B = U_C = U_Ф, можно записать комплексы фазных и линейных напряжений в виде:

; ; ; ; ; .

Приведенные соотношения, полученные из векторной диаграммы (рис.6), позволяют записать следующие равенства:


(1)

(2)


Нетрудно убедиться, рассмотрев, например, прямоугольный треугольник 0dq на рисунке 6, что линейное напряжение больше фазного в раз: U_Л =U_Ф.

При дальнейшем рассмотрении предполагается, как уже упоминалось ранее, что генератор трехфазного тока является идеальным источником (бесконечно большой мощности), у которого отсутствуют внутренние потери напряжения, то есть равны нулю сопротивления фаз.

Это означает, что такой генератор всегда вырабатывает симметричную систему фазных и линейных напряжений.

Кроме того, при выполнении лабораторных работ следует считать равными нулю сопротивления линейных проводов z_Л = 0 и нейтрального провода z_N = 0, а следовательно и потери напряжения в них.

С учетом принятых допущений можно утверждать, что на входные зажимы приемника a, b,c, соединенного звездой или треугольником, всегда подается симметричная система линейных напряжений, а при соединении приемника звездой (при наличии нейтрального провода) – симметричная система фазных напряжений генератора.

В этом случае электрические потенциалы линейных проводов будут равны потенциалам начал одноименных фаз генератора и приемника, а потенциал нейтрального провода будет равен потенциалам концов всех трех фаз генератора и приемника. Поэтому можно дать еще одно определение фазного и линейного напряжения для схемы «четырехпроводная звезда».

Фазным напряжением называется напряжение между линейным проводом и нейтральным проводом.

Линейным напряжением называется напряжение между двумя линейными проводами.

Режимы работы цепи при соединении генератора и приемника звездой

Режимы работы такой цепи определяются видом нагрузки, которую создает приемник для генератора, а также наличием или отсутствием нейтрального провода (он замкнут или разомкнут). Существуют два основных вида нагрузки: симметричная и несимметричная.

Симметричной называется нагрузка, при которой комплексные сопротивления фаз приемника равны друг другу, то есть Z_a = Z_b = Z_c = Z_Ф = z_Фe^jφ при соединении звездой и Z_ab = Z_bc = Z_ca = Z_Ф = z_Фe^jφ при соединении треугольником.

Это означает, что фазные токи в фазах приемника одинаковы по величине и сдвинуты по фазе относительно «своих» фазных напряжений на угол , где r_Ф и x_Ф соответственно активное и реактивное сопротивления фаз приемника.

Применительно к симметричному приемнику, соединенному звездой с нейтральным проводом, в соответствии с законом Ома можно записать комплексы действующих значений фазных (линейных) токов: =; =; =.

Согласно первому закону Кирхгофакомплекс тока в нейтральном проводе равен алгебраической сумме комплексов фазных токов:


(3)
,

то есть равен нулю, поскольку в ноль обращается выражение в скобках в соответствии с равенством (1). Таким образом при симметричной нагрузке токI_N= 0 и необходимостьв нейтральном проводе отпадает. Поэтому заведомо симметричные приемники, соединенные звездой (трехфазные асинхронные и синхронные двигатели и др.) подключаются к питающей сети тремя линейными проводами (по схеме «звезда без нейтрального провода»).

Несимметричной называется нагрузка, при которой комплексные сопротивления фаз приемника не равны друг другу: .

Очевидно в этом случае система фазных токов не может быть представлена в виде симметричной звезды векторов, как в предыдущем случае, вследствие чего в нейтральном проводе N–n (рис. 4) появляется ток I_N > 0. Это предполагает наличие разности электрических потенциалов между нейтральными точками генератора N и приемника n, которую можно измерить вольтметром, разомкнув нейтральный провод ().

Эта разность потенциалов получила название «напряжение смещения нейтрали U_N», комплексное выражение которого можно рассчитать по формуле:


(4)


где ; ; – комплексные проводимости фаз приемника;

– комплексная проводимость нейтрального провода.

Можно показать, что при несимметричном приемнике и разомкнутом нейтральном проводе (U_N > 0) фазные напряжения на приемнике U_a, U_b, U_c будут различаться по величине в соответствии с равенствами, полученными согласно второму законом Кирхгофа:


(5)
,

где – комплексы фазных напряжений генератора,

– комплекс напряжения смещения нейтрали.

Сравним равенства (5) при симметричной и несимметричной нагрузке при наличии нейтрального провода (Z_N = 0  ) и при его обрыве (Z_N   ).

Если нейтральный провод при несимметричном приемнике замкнут , то правая часть равенства (4) становится равной нулю , поскольку в знаменателе . Поэтому в соответствии с равенствами (5) система фазных напряжений приемника становится симметричной, как и в генераторе: , , .

Таким образом наличие нейтрального провода обеспечивает независимую работу фаз несимметричного приемника, поскольку напряжение на каждой фазе будет одним и тем же: , и изменение тока в каждой фазе скажется только на величине тока в нейтральном проводе.

Если нагрузка симметрична (), то U_N = 0, поскольку в ноль обращается числитель в формуле (4), и в соответствии с равенствами (5) система фазных напряжений приемника будет симметричной, имеется ли нейтральный провод или отсутствует.