Планирование доступа к вычислительным ресурсам лр 1 нгту. Лаба ОС 1. Планирование доступа к вычислительным ресурсам
 Скачать 353.84 Kb. Скачать 353.84 Kb.
|
|
МИНИСТЕРСТВО ВЫСШЕГО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ государственное БЮДЖЕТНОЕ образовательное учреждение высшего образования «НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра вычислительной техники  Отчёт по лабораторной работе №1 по дисциплине: «операционные системы» По теме: «Планирование доступа к вычислительным ресурсам» Выполнила:Проверил: «Доцент» «Коршикова Л.А.» « » __________ 2020г.« » __________2020г. _________________ _________________ (подпись) (подпись) Новосибирск 2020 Цель изучения темыИзучение и исследование некоторых алгоритмов и способов планирования заданий (с учетом требований к памяти и внешним устройствам) в мультипрограммной вычислительной системе. Исходные данныеВ таблице 1.5 приводятся характеристики задач, которые используются для моделирования планирования доступа к вычислительным ресурсам с целью операции – ЗАГРУЗКА. Таблица1.5 Характеристики задач
В таблице 1.6. приведены данные по варианту задания. Таблица1.6 Вариант задания
При выполнении работы использовались нижеприведенные списки задач, которые формируются с учетом данных таблиц. Согласно заданию, было составлено два списка задач (таблицы 1.7, 1.8). Каждый список задач запускался на системе с оперативной памятью размером 8, 12, 16 единиц и с постоянным количеством ВУ, равным 10. Списки задачТаблица1.7 Поток коротких задач
Таблица 1.8 Поток длинных задач
Результат выполнения работыВ результате моделирования функции операционной системы – планирование верхнего уровня – сформированы таблицы результатов 1.9. и 1.10. Таблица1.9. Зависимость коэффициента мультипрограммирования от ДО
Таблица1.10. Зависимость средневзвешенного времени от ДО
Анализ временных диаграммРассмотрим временную диаграмму 1 модели с максимальным коэффициентом мультипрограммирования (КМ) — 3. Дисциплина — PRT, тип поступления задач — поток, поцессорное время задач — длинное, количество оперативной памяти (ОП) — 12, количество вычислительных устройств ВУ — 10. Временная диаграмма мультипрограммной работы ВС при приведенных выше исходных данных изображена на рисунке 1.1 (О — ожидание, З — загрузка, П — очередь на выполнение). 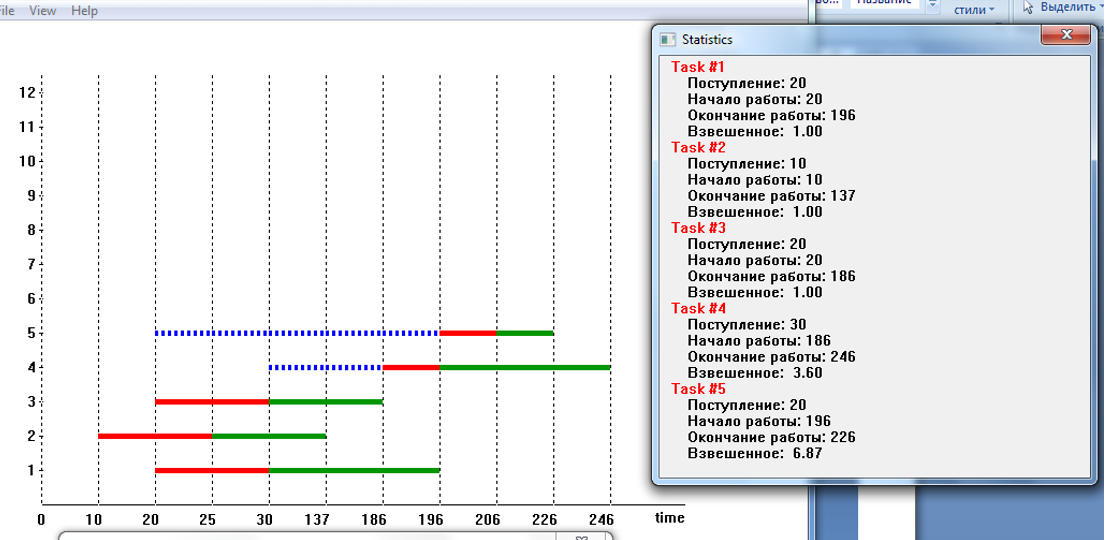 Рисунок 1. Временная диаграмма мультипрограммной работы ЭВМ для PRT Процесс построения временной диаграммы рассмотрен в табл. 1.11 Таблица1.10. Описание построения временной диаграммы
Проверка правильности построения временной диаграммыДля проверки правильности построения временной диаграммы необходимо определить по временной диаграмме, сколько времени работал процессор. Это временные интервалы с t = 25 до t = 246. Таким образом, процессор работал в течение 221 ед. времени. Далее необходимо просуммировать процессорное время всех выполненных заданий. 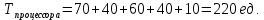 При анализе временной диаграммы время работы процессора должно было получиться 220 ед. времени, но на диаграмме мы видим 221 ед. времени. Лишняя единица во времени объясняется тем, что по ходу вычисления нам необходимо делить один промежуток времени на некоторые части. А из-за того, что разрядность типов данных с плавающей точкой ограничена, то при математических операциях с этими типами накапливается ошибка, которая, в конечном счете, и приводит к лишней единице в финальном результате. Для оценки эффективности дисциплины обслуживания найдем средневзвешенное время обращения:  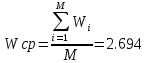 Рассмотрим временную диаграмму 2 модели с максимальным коэффициентом мультипрограммирования (КМ) — 2. Дисциплина — PRT, тип поступления задач — поток, поцессорное время задач — длинное, количество оперативной памяти (ОП) — 8, количество вычислительных устройств ВУ — 10. Временная диаграмма мультипрограммной работы ВС при приведенных выше исходных данных изображена на рисунке 1.1 (О — ожидание, З — загрузка, П — очередь на выполнение). 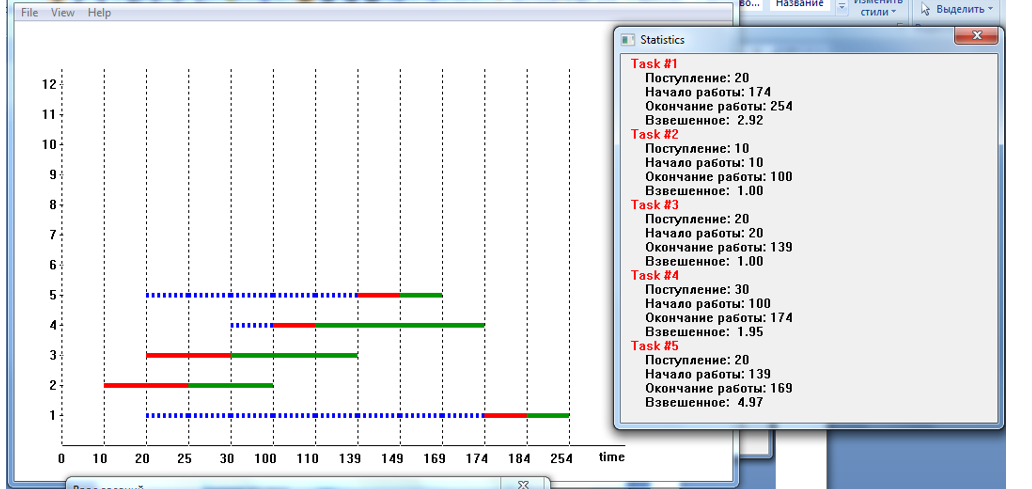 Рисунок 2. Временная диаграмма мультипрограммной работы ЭВМ для PRT Процесс построения временной диаграммы рассмотрен в табл. 1.13 Таблица1.14. Описание построения временной диаграммы
Проверка правильности построения временной диаграммыДля проверки правильности построения временной диаграммы необходимо определить по временной диаграмме, сколько времени работал процессор. Это временные интервалы с t = 25 до t = 254. Но в интервале с t = 174 до t = 184 был простой. Таким образом, процессор работал в течение 219 ед. времени. Далее необходимо просуммировать процессорное время всех выполненных заданий. 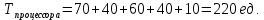 При анализе временной диаграммы время работы процессора должно было получиться 220 ед. времени, но на диаграмме мы видим 219 ед. времени. Лишняя единица во времени объясняется тем, что по ходу вычисления нам необходимо делить один промежуток времени на некоторые части. А из-за того, что разрядность типов данных с плавающей точкой ограничена, то при математических операциях с этими типами накапливается ошибка, которая, в конечном счете, и приводит к лишней единице в финальном результате. Для оценки эффективности дисциплины обслуживания найдем средневзвешенное время обращения:  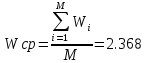 Сравнение дисциплин
Коэффициент мультипрограммированияИспользуя результаты таблицы 1.9. проанализируем зависимость коэффициента мультипрограммирования от количества ОП. В силу того, что для различных наборов задач (короткие – длинные) коэффициент мультипрограммирования меняется в малом диапазоне (2 – 4), удобнее изобразить соответствующие зависимости в виде трехмерной диаграммы (рис. 3). 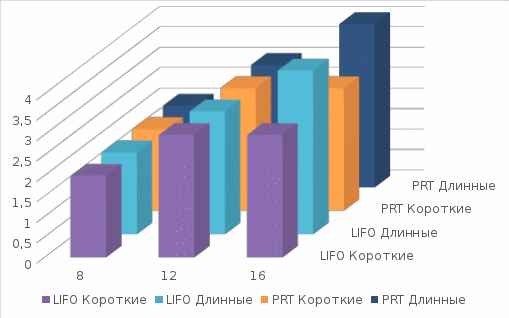 Рисунок 3 Зависимость коэффициента мультипрограммирования от количества ОП для составленных списков задач. Из рисунка 3. видно, что коэффициент мультипрограммирования для заданного потока коротких и длинных задач не зависят от дисциплины обслуживания (LIFO или PRT). С увеличением количества ОП с 8 до 12 единиц наблюдается увеличения коэффициента на 1 мультипрограммирования для пакета длинных задач, но при увеличении количества ОП с 12 до 16 единиц коэффициент мультипрограммирования тоже увеличивается на 1, и становится равным 4. В случае с коротким пакетом задач с увеличением количества ОП с 8 до 12 единиц наблюдается увеличения коэффициента мультипрограммирования с 2 до 3, а при увеличении количества ОП с 12 до 16 — не наблюдается увеличение коэффициента мультипрограммирования. Средневзвешенное времяИспользуя результаты таблицы 1.9. проанализируем зависимость средневзвешенного времени от количества ОП, представленную на рисунке 3. 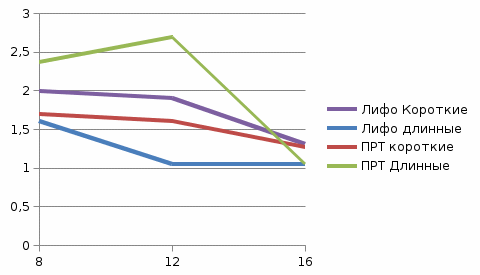 Рисунок 4. Зависимость средневзвешенного времени нахождения работ в системе от объема оперативной памяти. Из рисунка 4. видно, что c ростом количества ОП уменьшается средневзвешенное время выполнения задач. Дисциплина LIFO имеет меньшее средневзвешенное время выполнения задачи, чем дисциплина PRT, при работе с коротким потоком задач. С ростом количества ОП это преимущество незначительно уменьшается, т. к. задачи, требовательные к ОП могут выполняться одновременно. Говоря о длинных потоках задач, LIFO имеет меньшее средневзвешенное время выполнения задачи, чем дисциплина PRT, однако для ОП-16 они сравниваются. Дисциплина обслуживания PRT наиболее эффективна при использовании в длинных потоках и пакетах. Однако для достижения наименьшего средневзвешенного времени выполнения задачи необходимо задавать приоритеты в соответствии с параметрами системы, на которой эти задачи будут исполняться. Поэтому, скачек связан с самой особенностью службы PRT. Вывод В первой части лабораторной работы максимальный коэффициент мультипрограммирования равен – 4. Во второй части видно, что дисциплина PRT срабатывает для ОП-8 в моменты t = 20 и t= 100 и для ОП-12 в моменты t = 20 и t= 186. Соответственно скачек можно объяснить только самой особенностью службы PRT, так как она держала задачи долго в очереди. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
