Статистика. статистика. По данным ниже выполнить следующие пункты

• Название: По данным ниже выполнить следующие пункты
• Анкор: Статистика
• Дата: 08.12.2022
• Размер: 0.98 Mb.
• Имя файла: статистика.docx
• Тип: Документы; #834548

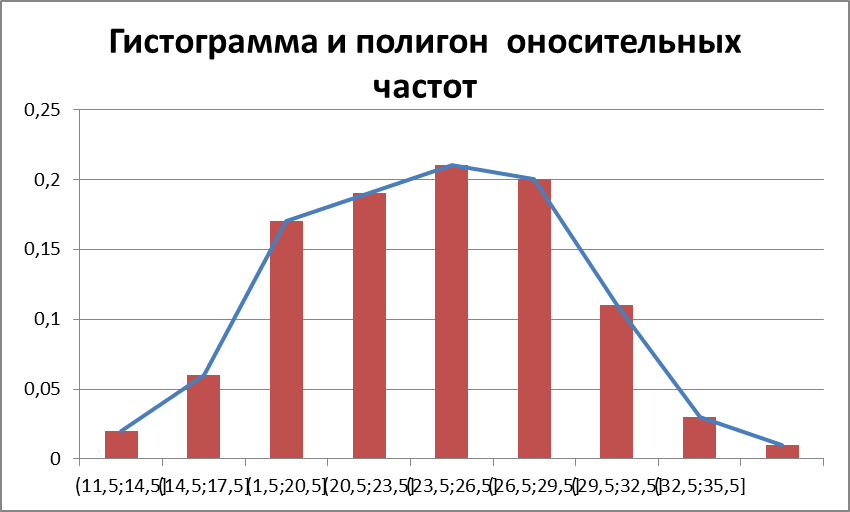
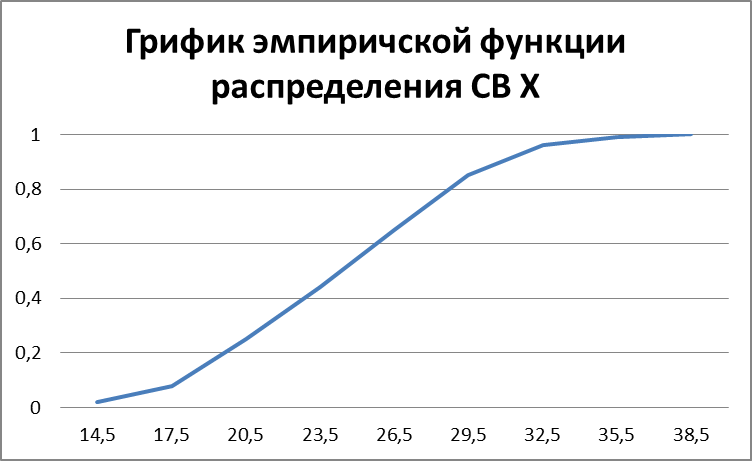
Задание 1. По данным ниже выполнить следующие пункты:

1. 
   Построить вариационный, статистический ряды и полигон относительных частот.
   
2. 
   Найти эмпирическую функцию распределения и построить ее график.
   
3. 
   Вычислить основные выборочные характеристики.
   
4. 
   Построить группированный статистический ряд.
   
5. 
   Вычислить основные характеристики группированного статистического ряда и сравнить их с характеристиками, найденными в пункте 3.
   
6. 
   Построить гистограмму относительных частот.
   
7. 
   Выдвинуть статистическую гипотезу H₀ о виде распределения генеральной совокупности; записать вид плотности f(x) и функции распределения F(x).
   
8. 
   На основе гипотезы, выдвинутой в пункте 7, методом моментов найти и вычислить оценки неизвестных параметров гипотетического распределения.
   
9. 
   Конкретизировать гипотезу H₀, построить график плотности f(x) совместно с гистограммой.
   
10. 
    Предполагая, что выдвинутая гипотеза H₀ верна, найти доверительные интервалы для неизвестных параметров с надежностью γ=0,99.
    
11. 
    На уровне значимости α = 1 –γ проверить согласованность гипотезы H₀ с эмпирическими данными по критерию согласия К. Пирсона.
    

6	2	8	7	3	3	2	6	11			3	5	8	4	7	3	6	7	6
8	10	5	3	10	2	12	4	4			6	3	8	4	8	7	7	3	7
2	4	5	6	3	4	6	10	8			10	7	3	5	7	8	5	7	7
9	6	0	-3	6	5	3	9	2			6	6	9	6	7	1	2	5	8
10	2	4	7	10	6	9	7	2			9	8	4	0	-4	5	9	9	2
0	1	3	3	5	4	5	5	3			0

Задание 2.

Изучая зависимость между показателями X и Y, проведено обследование 9 объектов и получены следующие данные

X	10	14	21	24	33	41	44	47	49
Y	43	47	50	48	54	57	61	59	65

Полагая, что между X и Y имеет место линейная корреляционная связь, определите выборочное уравнение регресси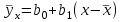и (или 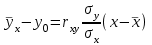) и выборочный коэффициент линейной регрессии . Постройте диаграмму рассеяния и линию регрессии. Сделайте вывод о направлении и тесноте связи между показателями X и Y.
Задача №1

Сделаем группировку наблюдаемых значений. Оптимальную длину интервала определим по формуле Стэрджеса:

Интервалы (a(i);a(i+1)]	Середины интервалов	Подсчет частот	Частоты n(i)	Относит.частоты W(i)=n(i)/n	Накопленные Относит.частоты
(11,5;14,5]				0,02	0,02
(14,5;17,5]				0,06	0,08
(17,5;20,5]				0,17	0,25
(20,5;23,5]				0,19	0,44
(23,5;26,5]				0,21	0,65
(26,5;29,5]				0,2	0,85
(29,5;32,5]				0,11	0,96
(32,5;35,5]				0,03	0,99
(35,5;38,5]				0,01

0,	если x <= 11,5
	0,08	если 11,5 <= x <=14,5
	0,25	если 14,5 <= x <= 17,5
	0,44	если 17,5 <= x<= 20,5
F(x)=	0,65	если 20,5 <= x <= 23,5
	0,85	если 23,5 <= x <= 26,5
	0,96	если 26,5 <= x <= 32,5
	0,99	если 32,5 <= x <= 35,5
		если 35,5 <= x <= 38,5

Середины интервалов y(i)	Частоты n(i)	y(i)-Y	(y(i)-Y)*n(i)	((y(i)-Y)^2)*n(i)	((y(i)-Y)^3)*n(i)	((y(i)-Y)^4)*n(i)
		-36,6	-73,20	2679,12	-98055,79	3588841,99
		-33,6	-201,60	6773,76	-227598,34	7647304,09
		-30,6	-520,20	15918,12	-487094,47	14905090,84
		-27,6	-524,40	14473,44	-399466,94	11025287,65
		-24,6	-516,60	12708,36	-312625,66	7690591,14
		-21,6	-432,00	9331,20	-201553,92	4353564,67
		-18,6	-204,60	3805,56	-70783,42	1316571,54
		-15,6	-46,80	730,08	-11389,25	177672,27
		-12,6	-12,60	158,76	-2000,38	25204,74
Сумма			-2532,00	66578,40	-1810568,16	50730128,93

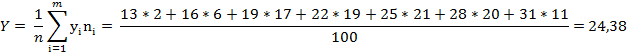Выборочная дисперсия:



Выборочное среднее квадратичное отклонение:



Выборочные коэффициенты асимметрии и эксцесса вычисляют по формулам: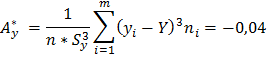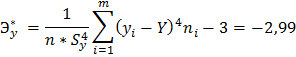









Где: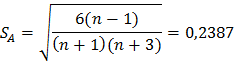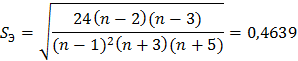





 

Итак, по совокупности указанных признаков можно предположить, что распределение СВ Y является нормальным.

Найти точечные оценки параметров нормального закона распределения, предполагая, что наблюдаемая случайная величина распределена по нормальному закону, и записать функцию плотности распределения вероятностей.



В качестве неизвестных параметров α и   возьмем их точечные оценки Y и S_yсоответственно.

Функция плотности:



Функция распределения вероятности: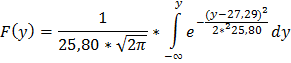



Задача № 2

Вспомогательная таблица имеет вид:

№	x	y	x2	y2	xy
1	10	43	100	1849	430	(-21,4)2=457,96	(-10,8)2=116,64	231,12
2	14	47	196	2209	658	(-17,4)2=302,76	(-6,8)2=46,24	118,35
3	21	50	441	2500	1050	(-10,4)2=108,16	(-3,8)2=14,44	39,52
4	24	48	576	2304	1152	(-7,4)2=54,76	(-5,8)2=33,64	42,92
5	33	54	1089	2916	1782	1,62=2,56	0,22=0,04	0,32
6	41	57	1681	3249	2337	9,62=92,16	3,22=10,24	30,72
7	44	61	1936	3721	2684	12,62=158,76	7,22=51,84	90,72
8	47	59	2209	3481	2773	15,62=243,36	5,22=27,04	81,12
9	49	65	2401	4225	3185	17,62=309,76	11,22=125,44	197,12
Всего	283	484	10629	26454	16051	1730,24	415,32	831,91
Среднее	31,4	53,8	1181	2939,3	1783,4

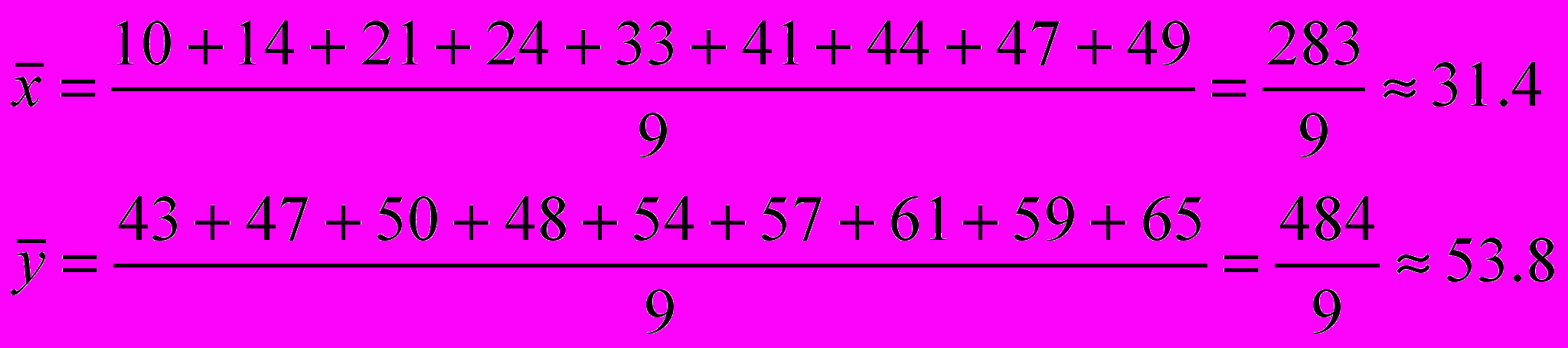Построим уравнение регрессии y=a+bx,коэффициенты a и b находим методом наименьших квадратов, решая систему линейных уравнений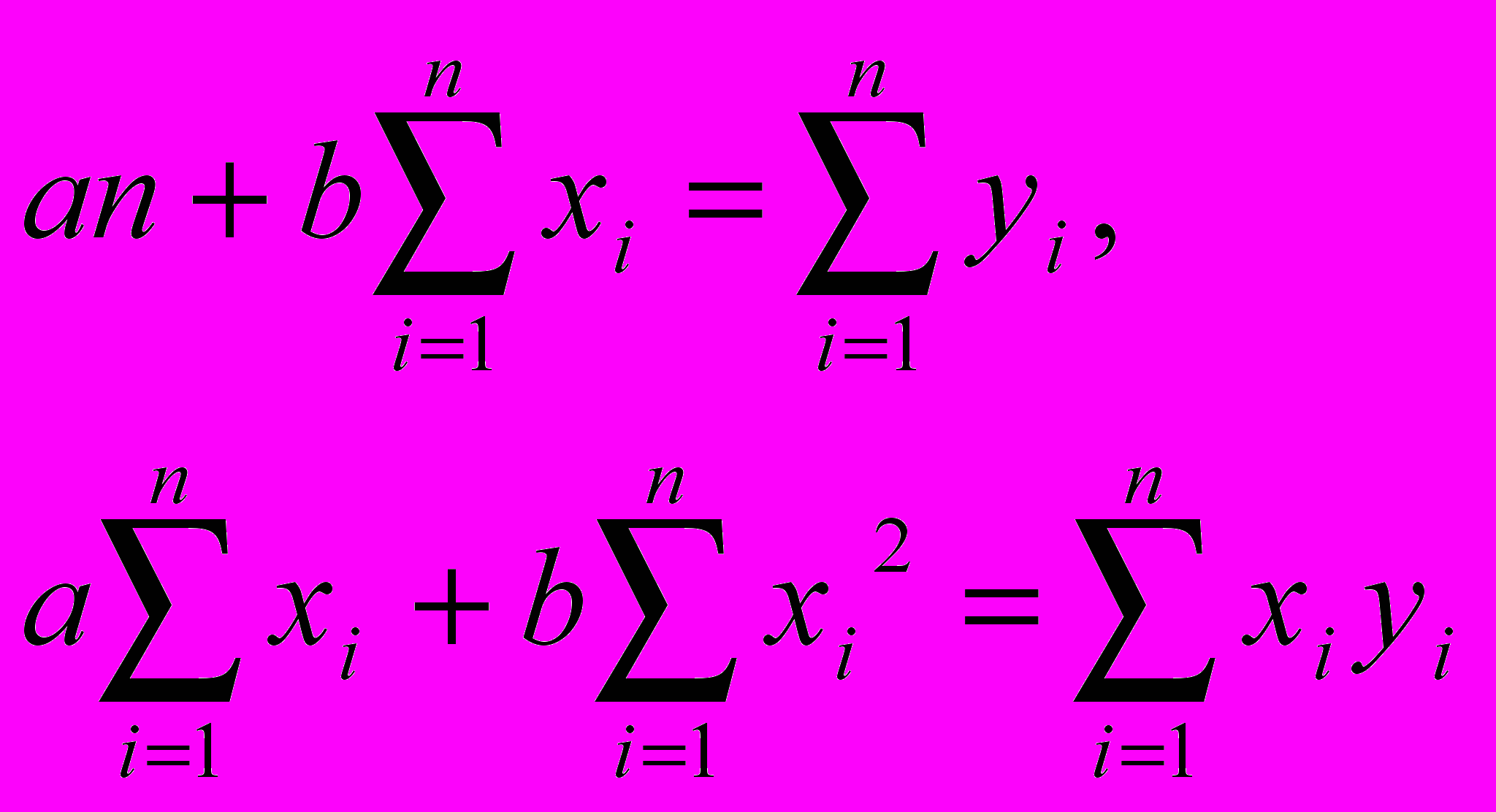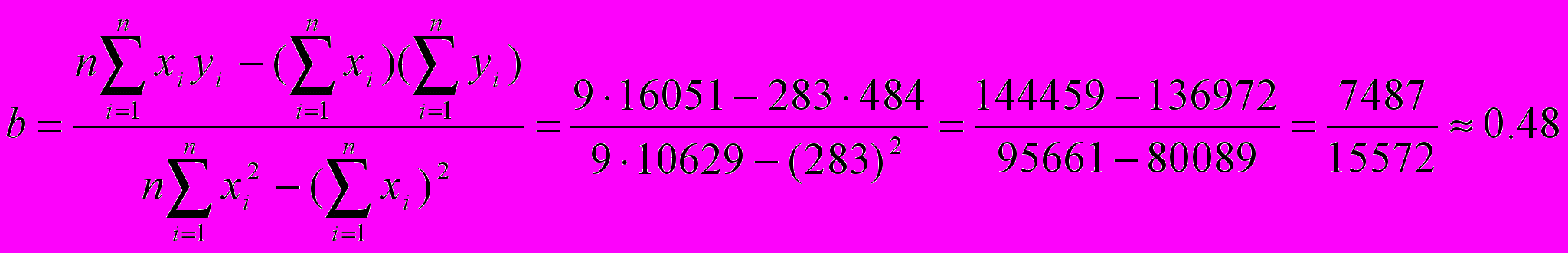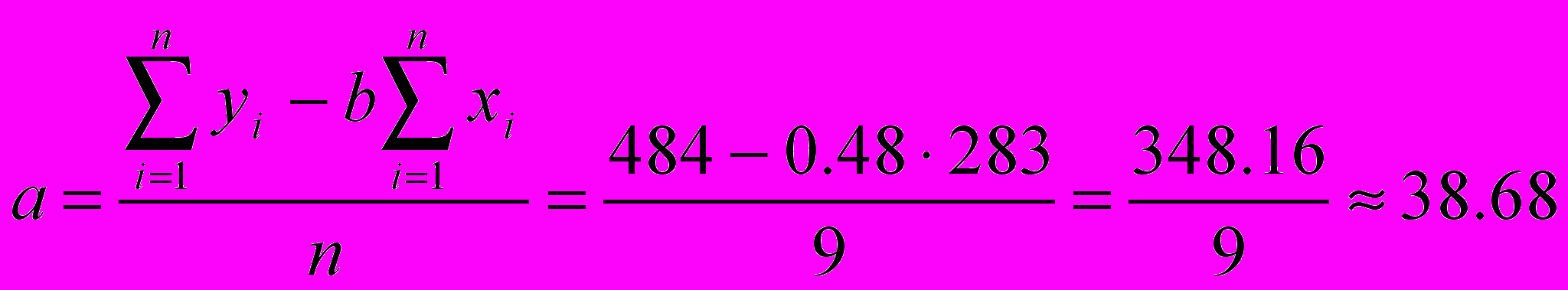




Уравнение регрессии имеет вид: yх=38.68+0.48x
Второе уравнение регрессии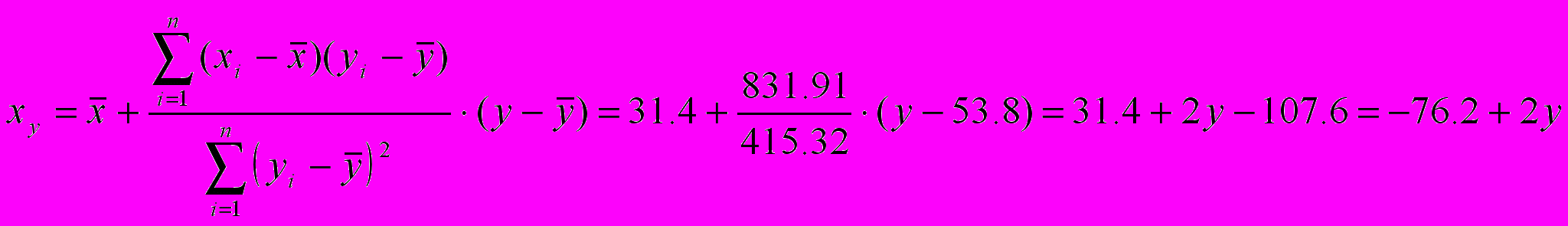

xy=-76.2+2y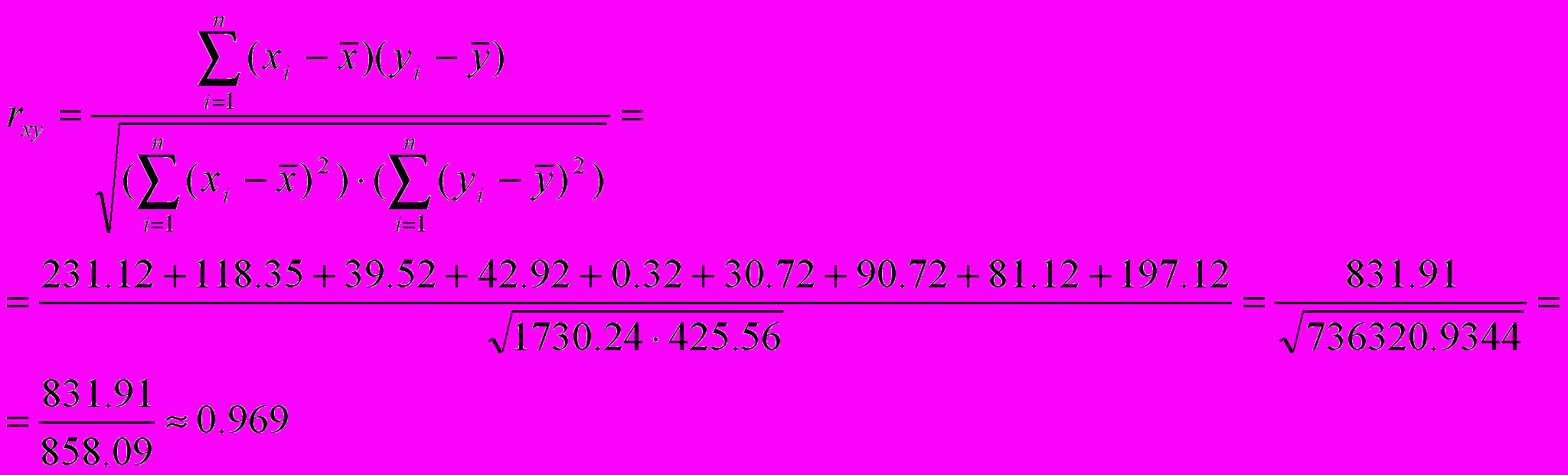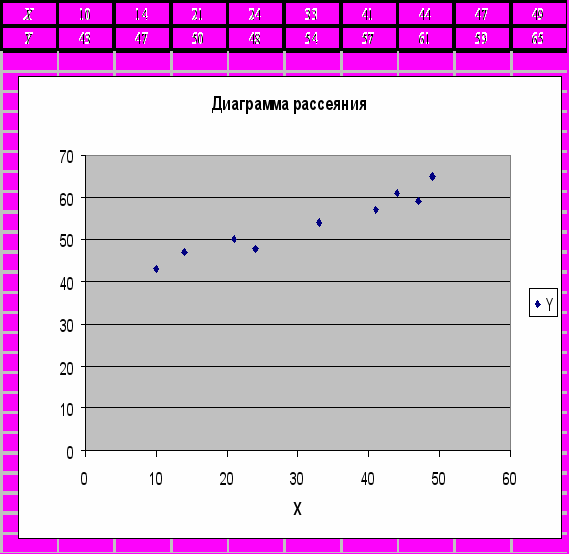




График линий регрессий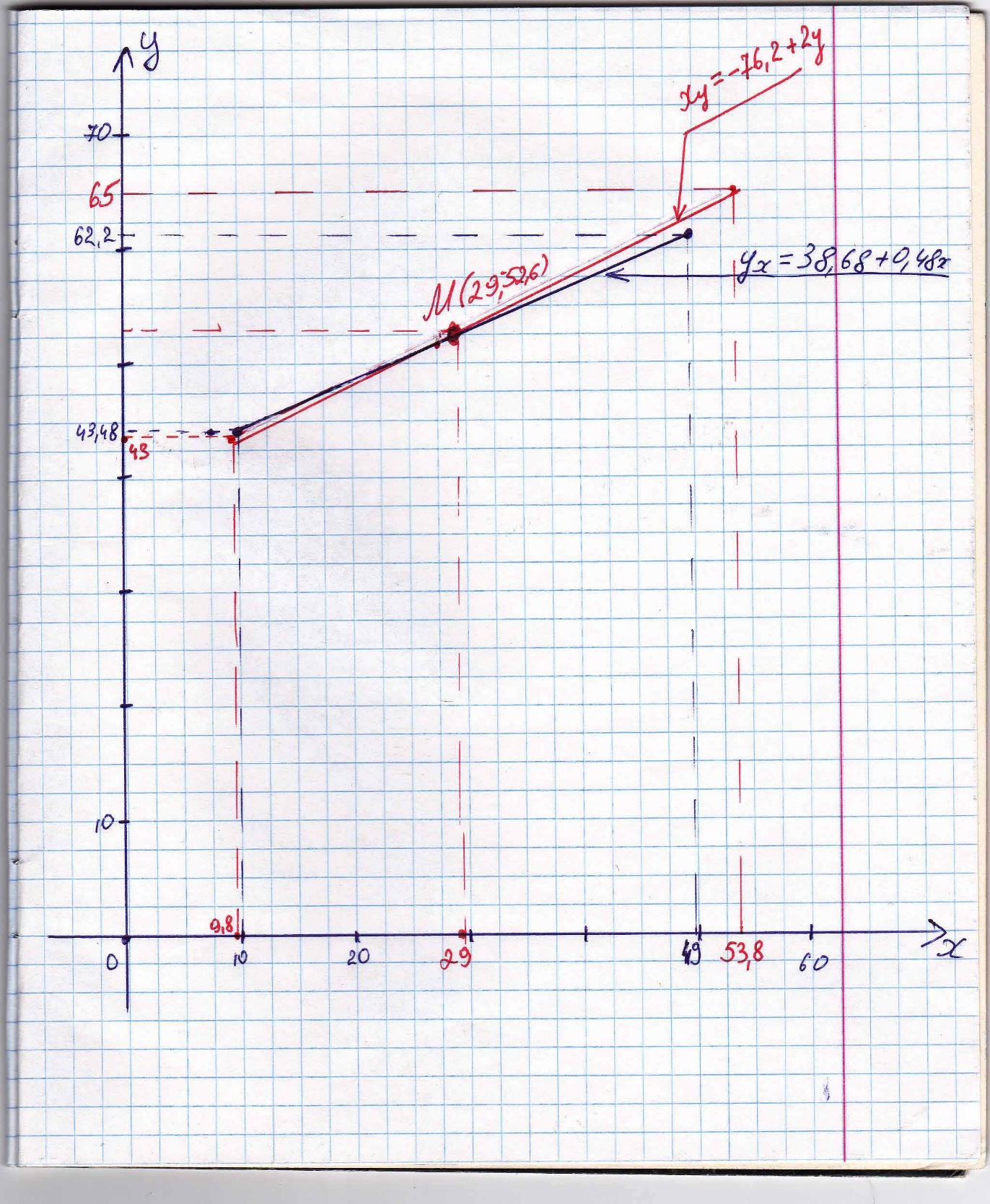

График линий регрессии отражает ряды теоретически ожидаемых значений функции по известным значениям аргумента. При этом, чем сильнее взаимосвязь между величинами xi и yi, тем меньше угол между линиями регрессии. В нашем случае r =0.969, линии уравнения регресии почти совпадают, так как корреляционная зависимость между признаками в этом случае переходит в функциональную.