Математические основы интеллектуальных технологий_задание 3. По учебному курсу Математические основы интеллектуальных технологий
 Скачать 0.91 Mb.
|
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования «Тольяттинский государственный университет» Институт математики, физики и информационных технологий
Практическое задание №3 по учебному курсу «Математические основы интеллектуальных технологий»(наименование учебного курса) Вариант 5 (при наличии)
Тольятти 2022 Практическое задание 3Лекция 2.1. Основы теории нечетких множествЗадано нечеткое множество А. x – непрерывный носитель нечеткого множества с диапазоном значений [K; N]. Для нечеткого множества А задана функция принадлежности: μА(x) = T·| (B·sin(x))C – D·x |. Обозначения: | | – модуль, С – степень. Требуется определить высоту нечеткого множества А. Ответ округлить до двух знаков после запятой и записать со знаком «запятая». Например, если при расчете получилось «–12,325», то ответ надо записывать как «–12,33». Таблица 1
Вариант 5 Исходные данные: K = 0; N = 8; B = 9,5; C = 0,1; D = 0,1; T = 0,7. Бланк выполнения задания 3 Определение: Величина sup μА(х) называется высотой нечеткого множества А. Параметры функции принадлежности: T= 0,7 B= 9,5 C= 0,1 D= 0,1 Введём обозначения: a=T*B^C= 0,7*9,5^0.1=0,8767391511 k=T*D=0,7*0,1=0,07 В этих обозначениях функция принадлежности принимает вид: mA(x)= |a*sinC(x)-k*x| На заданном отрезке [0; 8] непрерывная функция достигает максимума. Чтобы найти его, мы сначала рассмотрим функцию без модуля: y(x)= a*sinC(x)-k*x Рассмотрим её поведение на графике: 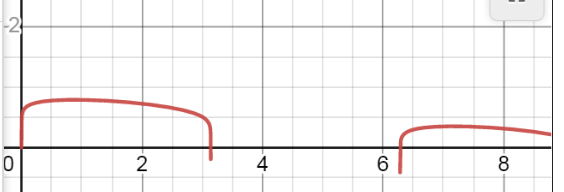 На промежутке, где синус отрицателен возведение в степень 1/10 невозможно. Для поиска максимума можно ограничиться промежутком [0; 2], где y(x) неотрицательна и совпадает с модулем. Найдём производную и приравняем её к нулю. y'(x)= a*C*(sinC-1(x))*cos(x) - k = 0 П 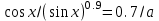 осле подстановки численных значений имеем уравнение:
|