погрешности классы точности (1). Погрешности измерений и средств измерений
 Скачать 59.29 Kb. Скачать 59.29 Kb.
|
|
Погрешности измерений и средств измерений Погрешность средств измерений – разность между показанием средства измерения и истинным (действительным) значением измеряемой физической величины. Для меры показанием является ее номинальное значение (пример меры – гирьки весов). Номинальным значением средства измерения является значение физической величины, определенное в соответствии с паспортом средства измерения. Истинное значение физической величины неизвестно, поэтому на практике пользуются действительным значением физической величины. Действительное значение физической величины можно максимально приблизить к истинному, тщательно проводя измерения на поверенных средствах измерений и последующей математической обработкой полученных результатов. Для сравнительной оценки средств измерений используется понятие «точность» средства измерений – это характеристика качества средства измерений, отражающая близость его погрешности к нулю. Погрешности средств измерений по форме числового выражения Абсолютная погрешность – это отклонение результата измерения Xи от истинного (или действительного) значения Xд измеряемой величины. Абсолютная погрешность выражается в единицах измеряемой физической величины: ΔX = Xи – Xд, где XИ – измеренная величина; XД – действительная величина. Измерение действительного значения производится с помощью образцового прибора или воспроизводится мерой, или рассчитывается при статистической обработке результатов нескольких измерений. По зависимости абсолютной погрешности от значений измеряемой величины дополнительно различают погрешности: аддитивные Δa, не зависящие от измеряемой величины; мультипликативные Δм, которые прямо пропорциональны измеряемой величине, и нелинейные Δн, имеющие нелинейную зависимость от измеряемой величины. Аддитивные погрешности не зависят от измеряемой величины X, а мультипликативные – прямо пропорциональны значению X. Источники аддитивной погрешности – трение в опорах, неточность отсчета, шум, наводки и вибрации. От этой погрешности зависит наименьшее значение величины, которое может быть измерено прибором. Причина мультипликативных погрешностей – влияние внешних факторов и старение элементов и узлов приборов. Абсолютная погрешность не может в полной мере служить показателем точности измерений, так как одно и то же ее значение, например, Δ Х = 0,05 м при Х =100 м, соответствует достаточно высокой точности измерений, а при Х = 1 м – низкой. Поэтому и вводится понятие относительной погрешности. Относительная погрешность – это отношение абсолютной погрешности к действительному или измеренному значению измеряемой величины. Относительную погрешность выражают в процентах: 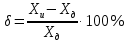 , или , или 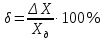 , ,где XИ – измеренная величина; XД – действительная величина. Чем меньше относительная погрешность, тем точнее измерение. Однако относительная погрешность не годится для нормирования погрешности средств измерений, так как при изменении значений Х, относительная погрешность принимает различные значения вплоть до бесконечности при Хд = 0. Поэтому для указания и нормирования погрешности средств измерений используется еще одна разновидность погрешности – приведенная. Приведенная погрешность – относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины (нормирующему значению), постоянному во всем диапазоне измерений или в его части. Приведенную погрешность выражают в процентах и определяют по формуле: 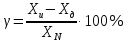 , или , или 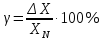 , ,где XN – нормирующее значение измеряемой величины. Чаще всего за нормирующее значение XN принимают верхний предел измерений данного средства измерений, применительно к которому и используется главным образом понятие «приведенная погрешность». Если диапазон измерений средства измерения лежит в положительной и отрицательной областях, то за нормирующее значение обычно принимают сумму модулей пределов измерений, например, для термометра с диапазоном измерений от «минус» 50 °С до «плюс» 50 °С, нормирующее значение будет равняться |50 °С| + |– 50 °С)| = 100 °C. Пример решения задачи Задача Вольтметром со шкалой (0…100) В, имеющим абсолютную погрешность ∆V = 1 В, измерены значения напряжения 0; 10; 20; 40; 50; 60; 80; 100 В. Рассчитать зависимость относительной и приведённой погрешностей от результата измерений. Решение Для записи результатов формируем таблицу, в столбцы которой будем записывать измеренные значения V, абсолютные ∆V, относительные δV и приведённые γV погрешности. В первый столбец записываем заданные в условии задачи измеренные значения напряжения: 0; 10; 20; 40; 50; 60; 80; 100 В. Значение абсолютной погрешности известно из условий задачи (∆V = 1 В) и считается одинаковым для всех измеренных значений напряжения; это значение заносим во все ячейки второго столбца. Значения относительной погрешности будем рассчитывать по формуле: 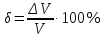 При V = 0 В 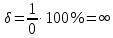 При V = 10 В 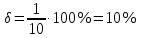 и так далее. и так далее.Полученные таким образом значения относительной погрешности заносим в третий столбец. Для расчёта значений приведённой погрешности будем использовать формулу: 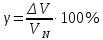 Предварительно определим нормирующее значение VN. Так как диапазон измерений вольтметра – (0…100) В, то шкала вольтметра содержит нулевую отметку, следовательно, за нормирующее значение принимаем размах шкалы прибора, т.е. 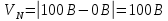 Так как величины ∆V и VN постоянны при любых измеренных значениях напряжения, то величина приведённой погрешности так же постоянна и составляет: 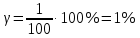 Это значение заносим во все ячейки четвертого столбца.
Класс точности средств измерений и его обозначение Класс точности средств измерений – это обобщенная характеристика данного типа средств измерений, отражающая уровень их точности, выражаемая пределами допускаемой основной, а в некоторых случаях и дополнительных погрешностей, а также другими характеристиками, влияющими на точность. Класс точности применяется для средств измерений, используемых в технических измерениях, когда нет необходимости или возможности выделить отдельно систематические и случайные погрешности, оценить вклад влияющих величин с помощью дополнительных погрешностей. Класс точности не является непосредственной оценкой точности измерений, выполняемых этим средством измерения, поскольку погрешность зависит еще от ряда факторов: метода измерений, условий измерений и т.д. Класс точности лишь позволяет судить о том, в каких пределах находится погрешность средств измерений данного типа. Класс точности средств измерений конкретного типа устанавливают в стандартах технических требований или других нормативных документах. Средство измерения может иметь два и более класса точности. Например, при наличии у него двух или более диапазонов измерений одной и той же физической величины ему можно присваивать два или более класса точности. Приборы, предназначенные для измерения нескольких физических величин, также могут иметь различные классы точности для каждой измеряемой величины. Пределы допускаемой основной погрешности ΔСИ, определяемые классом точности, – это интервал, в котором находится значение основной погрешности средств измерений. Пределы допускаемых основной и дополнительной погрешностей могут быть выражены в форме приведенных, относительных или абсолютных погрешностей. Выбор формы представления зависит от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения средств измерений. Выражение пределов допускаемой основной погрешности в форме абсолютной погрешности. Пределы допускаемой абсолютной основной погрешности устанавливаются по одной из формул: ΔХ = ±а или ΔХ = ± (а + bХ), где Х – значение измеряемой величины или число делений, отсчитанное по шкале; а, b – положительные числа, не зависящие от Х. Первая формула описывает только аддитивную погрешность, а вторая – сумму аддитивной и мультипликативной погрешностей соответственно. В технической документации классы точности, установленные в виде абсолютных погрешностей, обозначают прописными буквами латинского алфавита или римскими цифрами, причём меньшие пределы погрешностей должны соответствовать буквам, находящимся ближе к началу алфавита, или меньшим цифрам. Выражение пределов допускаемой основной погрешности в форме относительной погрешности. Если абсолютная погрешность задается формулой ΔХ = ±a, пределы допускаемой относительной основной погрешности определяются по формуле: δ = ΔХ / Хд = ±q, где q отвлеченное положительное число, выбираемое из ряда значений: (1; 1,5; 2; 2,5; 4; 5; 6)⋅10n; n =1; 0; «минус» 1; «минус» 2;….. Класс точности на прибор обозначается в виде В случае если абсолютная погрешность задается формулой ΔХ = ± а +(bХ) пределы допускаемой относительной основной погрешности определяются по формуле: 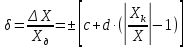 где с, d – отвлеченные положительные числа, выбираемые из ряда: (1; 1,5; 2; 2,5; 4; 5; 6)⋅10n; n =1; 0; «минус» 1; «минус» 2;….. причем с > d; Хk – больший (по модулю) из пределов измерений; Х – значение измеряемой величины. Первое слагаемое в этой формуле имеет смысл относительной погрешности при Х = Хk и отвечает за мультипликативную составляющую погрешности, второе – характеризует рост относительной погрешности при уменьшении показаний прибора и отвечает за аддитивную составляющую погрешности. При использовании данной формулы класс точности обозначается в виде «0,02/0,01», где числитель – это конкретное значение числа «с», знаменатель – числа «d». Данный способ задания класса точности применяется для приборов с соизмеримыми аддитивными и мультипликативными погрешностями Выражение пределов допускаемой основной погрешности в форме приведенной погрешности. Пределы допускаемой приведенной основной погрешности определяются по формуле: γ = ΔХ / ХN = ± p, где ХN – нормирующее значение, выраженное в тех же единицах, что и Δ; р – отвлеченное положительное число, выбираемое из ряда значений: (1; 1,5; 2; 2,5; 4; 5; 6)⋅10n; n =1; 0; «минус» 1; «минус» 2;…. . Нормирующее значение ХN устанавливается равным большему из пределов измерений (или модулей) для средств измерений с равномерной, практически равномерной или степенной шкалой и для измерительных преобразователей, для которых нулевое значение выходного сигнала находится на краю или вне диапазона измерений. Для средств измерений, шкала которых имеет условный нуль, ХN равно сумме модулей пределов измерений. Для приборов с существенно неравномерной шкалой ХN принимают равным всей длине шкалы или ее части, соответствующей диапазону измерений. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах длины, а на средстве измерений класс точности условно обозначают, например, в виде значка В остальных случаях класс точности обозначают конкретным числом р, например, 1,5. Обозначение наносится на циферблат, щиток или корпус прибора. Правила построения и примеры обозначения классов точности в документации и на средствах измерений приведены в таблице. Таблица Обозначение классов точности и средств измерений
Примеры решения задач Задача 1. Амперметром класса точности 2,0 со шкалой (0…50) А измерены значения тока 0; 5; 10; 20; 25; 30; 40; 50 А. Рассчитать зависимости абсолютной, относительной и приведённой основных погрешностей от результата измерений. Решение Для записи результатов формируем таблицу, в столбцы которой будем записывать измеренные значения I, абсолютные ∆I, относительные δI и приведённые γI погрешности. В первый столбец записываем заданные в условии задачи измеренные значения тока: 0; 5; 10; 20; 25; 30; 40; 50 А. Класс точности амперметра задан числом без кружка, следовательно, приведённая погрешность, выраженная в процентах, во всех точках шкалы не должна превышать по модулю класса точности, т.е. |γI | ≤ 2%. При решении задачи рассмотрим худший случай | γI | = 2%, когда приведённая погрешность принимает максимальное по абсолютной величине значение, что соответствует γI = +2% и γI = –2%. Данные значения приведённой погрешности заносим в четвёртый столбец таблицы. Рассчитаем значения абсолютной погрешности. Из формулы 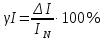 выражаем абсолютную погрешность выражаем абсолютную погрешность 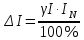 За нормирующее значение IN принимаем размах шкалы, так как шкала амперметра содержит нулевую отметку, т.е. IN = |50 А – 0 А| = 50 А. Абсолютная погрешность равна: 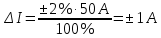 во всех точках шкалы прибора. Заносим данное значение во второй столбец таблицы. во всех точках шкалы прибора. Заносим данное значение во второй столбец таблицы. Значения относительной погрешности будем рассчитывать по формуле: 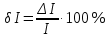 При I = 0 A 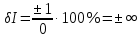 При I = 10 A 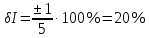 и так далее. и так далее.
Задача 2. Цифровым омметром класса точности 1,0/0,5 со шкалой (0…1000) Ом измерены значения сопротивления 0; 100; 200; 400; 500; 600; 800; 1000 Ом. Рассчитать зависимости абсолютной и относительной основных погрешностей от результата измерений. Решение Для записи результатов формируем таблицу, в столбцы которой будем записывать измеренные значения R, абсолютные ∆R и относительные δR погрешности. В первый столбец записываем заданные в условии задачи измеренные значения сопротивления 0; 100; 200; 400; 500; 600; 800; 1000 Ом. Класс точности вольтметра задан в виде двух чисел, разделённых косой чертой. Следовательно, относительная погрешность, выраженная в процентах, во всех точках шкалы должна удовлетворять следующему соотношению: 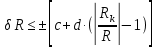 В данном случае c = 1,0; d = 0,5; Rк = 1000 Ом, причём параметры этой формулы «c» и «b» определяются мультипликативной и аддитивной составляющими суммарной погрешности соответственно. Таким образом, получаем: 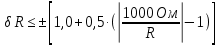 При решении задачи рассмотрим худший случай: 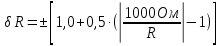 Рассчитаем значения относительной погрешности. При R = 0 Ом получаем 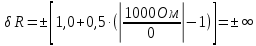 При R = 100 Ом получаем 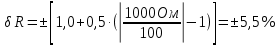 и так далее. и так далее.Полученные значения относительной погрешности заносим в третий столбец таблицы. Рассчитаем значения абсолютной погрешности. Из формулы относительной погрешности 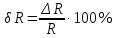 выражаем абсолютную погрешность: выражаем абсолютную погрешность: 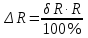 И при R = 0 Ом получаем 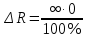 – неопределенность, в этом случае искомое значение ∆R можно определить следующим образом. Так как класс точности прибора задан в виде двух чисел, то у данного прибора аддитивные и мультипликативные погрешности соизмеримы. При R = 0 Ом мультипликативная составляющая погрешности равна нулю, значит, общая погрешность в этой точке обусловлена только аддитивной составляющей. Аддитивную составляющую представляет второе из чисел, задающих класс точности, т.е. в данном случае число «d» = 0,5. Это означает, что аддитивная погрешность составляет 0,5 % от верхнего предела измерений прибора, т.е. от Rк = 1000 Ом. – неопределенность, в этом случае искомое значение ∆R можно определить следующим образом. Так как класс точности прибора задан в виде двух чисел, то у данного прибора аддитивные и мультипликативные погрешности соизмеримы. При R = 0 Ом мультипликативная составляющая погрешности равна нулю, значит, общая погрешность в этой точке обусловлена только аддитивной составляющей. Аддитивную составляющую представляет второе из чисел, задающих класс точности, т.е. в данном случае число «d» = 0,5. Это означает, что аддитивная погрешность составляет 0,5 % от верхнего предела измерений прибора, т.е. от Rк = 1000 Ом. Таким образом, при R = 0 имеем: 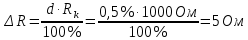 Далее при R = 100 Ом получаем: 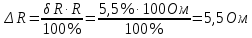 При R = 200 Ом получаем: 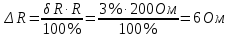 и так далее. и так далее.Полученные таким образом значения абсолютной погрешности заносим во второй столбец таблицы.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||