Шпаргалка по теме пределы. пределы. Последовательности. Предел функции. Предел последовательности
 Скачать 57.82 Kb. Скачать 57.82 Kb.
|
|
Тема: Последовательности. Предел функции. Предел последовательности. Числовая последовательность – совокупность всех элементов 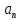 , где число , где число 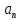 называется элементами, а само число n – номер элемента последовательности. (обозначение: называется элементами, а само число n – номер элемента последовательности. (обозначение: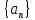 , n=1,2,3… или , n=1,2,3… или 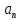 , n=1,2,3…) , n=1,2,3…)Число 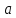 называется пределом числовой последовательности называется пределом числовой последовательности 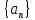 , если , если 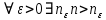 будет справедливо равенство будет справедливо равенство 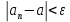 . . 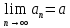
Арифметические свойства пределов: 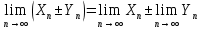 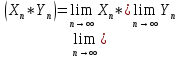 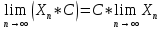 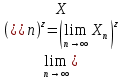 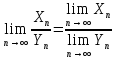
Свойства: 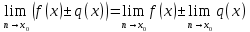 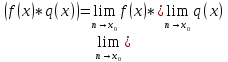 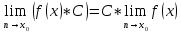 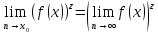 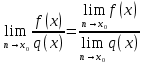
Пусть 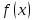 определена в определена в 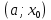 (соответственно (соответственно 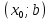 ). Число B называется пределом функции ). Число B называется пределом функции 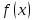 слева в слева в 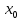 (справа (справа 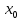 ), если ), если 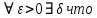 для всех для всех 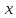 таких что таких что 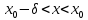 (соответственно (соответственно 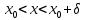 ) выполняется неравенство ) выполняется неравенство 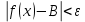 . Пределы справа и слева называются односторонними. . Пределы справа и слева называются односторонними.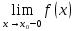 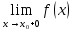
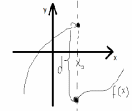
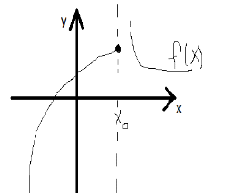
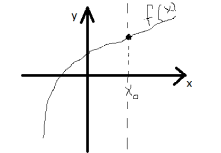
Пусть функция 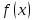 определена для всех определена для всех 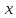 из интервала из интервала 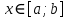 ,за исключением быть может точки ,за исключением быть может точки 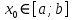 . Тогда . Тогда 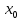 называется точкой разрыва называется точкой разрыва 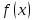 , если функция не определена в этой точке или если функция не является непрерывной в этой точке. , если функция не определена в этой точке или если функция не является непрерывной в этой точке.
 Запомнить! 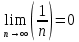 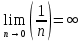 | |||||||||||||||||||||||||||||||||||||

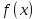 в точке
в точке 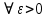 , найдётся такое число
, найдётся такое число 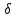 , что для всех
, что для всех 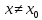 удовлетворяющих условию, что
удовлетворяющих условию, что 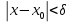 , выполняется неравенство
, выполняется неравенство 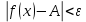
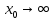 , если
, если 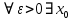 такое что для всех
такое что для всех 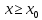 будет справедливо неравенство
будет справедливо неравенство 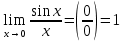
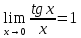
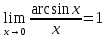
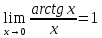
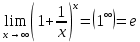
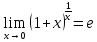
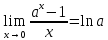
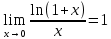
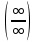
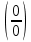
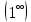
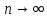 )
)