графики функций 9 класс. 9 класс конспект график функции. Построение графиков функций путем преобразования
 Скачать 3.08 Mb. Скачать 3.08 Mb.
|
|
Презентация на тему: Построение графиков функций путем преобразования   Цели урока: Повторить способы преобразования графиков функций. Проверить знания учащихся.  Преобразования: 1. y = f(x – a) 2. y = f(x) + b 3. y = - f(x) 4. y = f(-x) 5. y = kf(x), где k>0 6. y = f(kx), где k>0 7. y = |f(x)| 8. y = f(|x|) 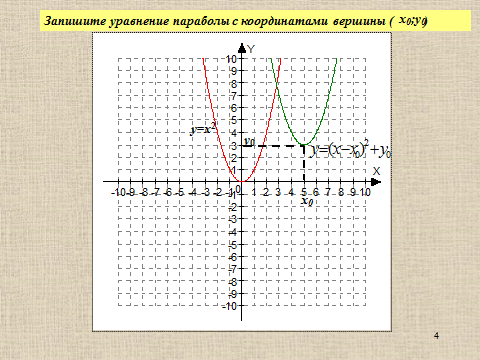 Запишите уравнение параболы с координатами вершины (x0 ;y)  Параллельный перенос (сдвиг). Рассмотрим параллельный перенос вдоль оси абсцисс. Пусть дан график функции y = f(x). Как по отношению к нему будет расположен график функции y = f(x – a), a>0 ? 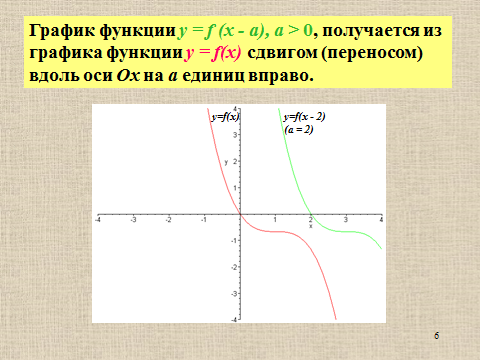 График функции y = f (x - a), a > 0, получается из графика функции y = f(x) сдвигом (переносом) вдоль оси Ох на а единиц вправо. 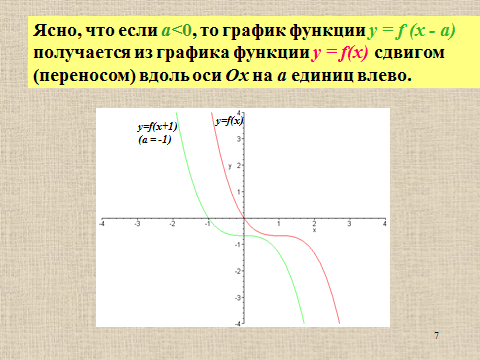 Ясно, что если а<0, то график функции y = f (x - a) получается из графика функции y = f(x) сдвигом (переносом) вдоль оси Ох на а единиц влево. 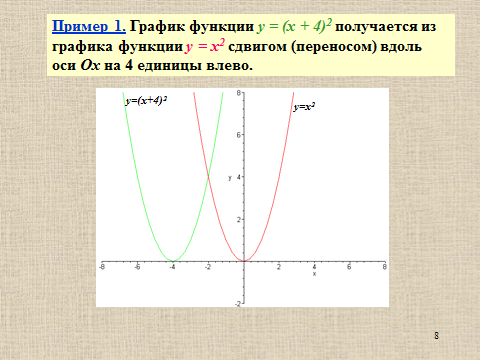 Пример 1. График функции 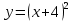 получается из графика функции получается из графика функции 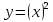 сдвигом (переносом) вдоль оси Ох на 4 единицы влево. сдвигом (переносом) вдоль оси Ох на 4 единицы влево.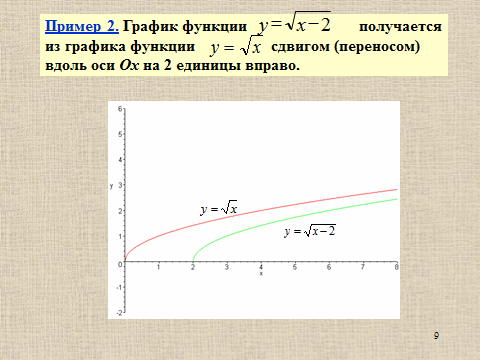 Пример 2. График функции 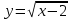 получается из графика функции получается из графика функции 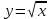 сдвигом (переносом) вдоль оси Ох на 2 единицы вправо. сдвигом (переносом) вдоль оси Ох на 2 единицы вправо. Рассмотрим теперь параллельный перенос вдоль оси ординат. В этом случае график функции y = f(x) + b получается из графика функции y=f(x) при b > 0 смещением на b единиц вверх, а при b < 0 – на |b| единиц вниз. 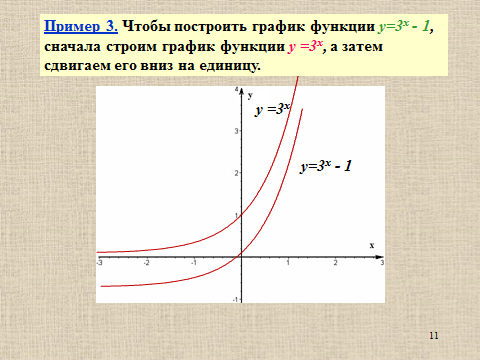 Пример 3. Чтобы построить график функции 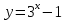 , сначала строим график функции , сначала строим график функции 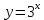 , а затем сдвигаем его вниз на единицу. , а затем сдвигаем его вниз на единицу.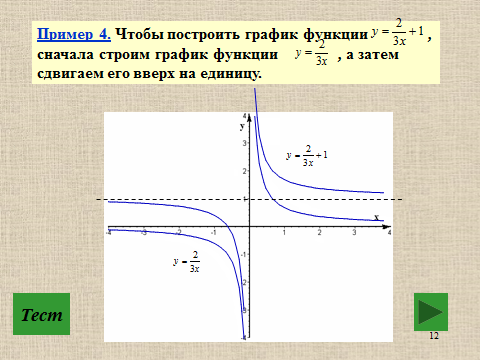 Пример 4. Чтобы построить график функции 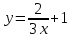 , сначала строим график функции , сначала строим график функции 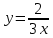 , а затем сдвигаем его вверх на единицу. Тест , а затем сдвигаем его вверх на единицу. Тест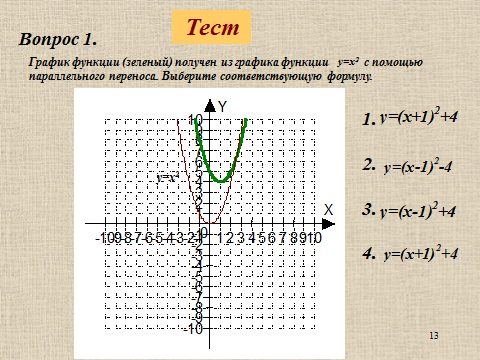 Тест. Вопрос 1. График функции (зеленый) получен из графика функции 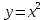 с помощью параллельного переноса. Выберите соответствующую формулу. с помощью параллельного переноса. Выберите соответствующую формулу.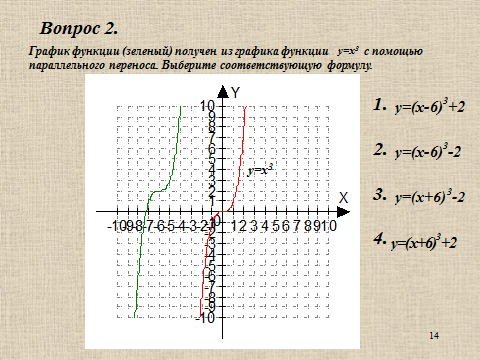 Вопрос 2. График функции (зеленый) получен из графика функции 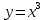 с помощью параллельного переноса. Выберите соответствующую формулу. с помощью параллельного переноса. Выберите соответствующую формулу. 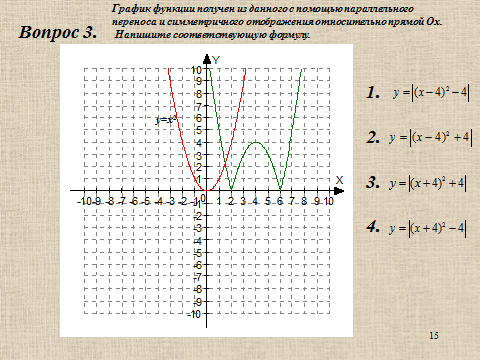 Вопрос 3. График функции получен из данного с помощью параллельного переноса и симметричного отображения относительно прямой Ох. Напишите соответствующую формулу.  2. Деформация (растяжение и сжатие) графика. График функции у = f(ω·x), ω>0, получается из графика функции у = f(x), «сжатием» к оси у в ω раз при ω>1 и «растяжением» от оси у в раз при 0<ω<1. График функции у = k·f(x), k>0, получается из графика функции у = f(x), «растяжением» от оси х в k раз при k>1 и «сжатием» к оси х в раз при 0< k<1. 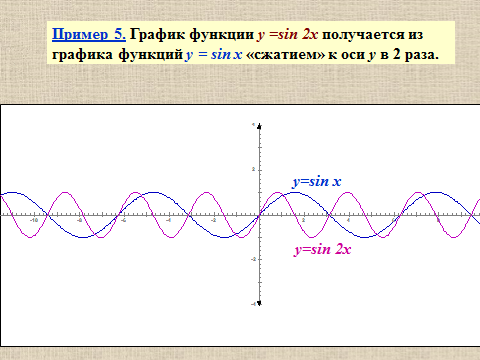 Пример 5. График функции y =sin 2x получается из графика функций y = sin x «сжатием» к оси у в 2 раза. 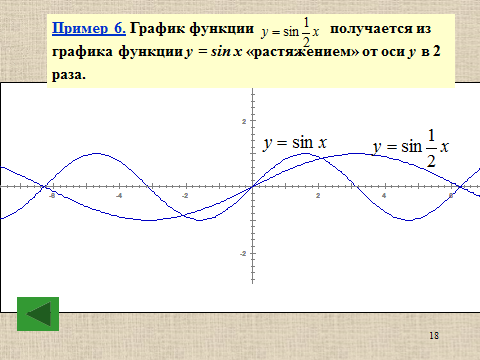 Пример 6. График функции 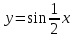 получается из графика функции получается из графика функции 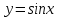 «растяжением» от оси у в 2 раза. «растяжением» от оси у в 2 раза. 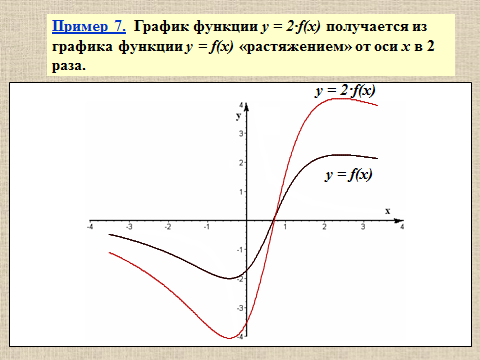 Пример 7. График функции y = 2·f(x) получается из графика функции y = f(x) «растяжением» от оси х в 2 раза. 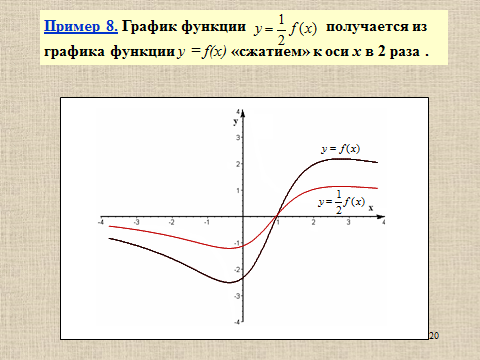 Пример 8. График функции 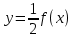 получается из графика функции получается из графика функции 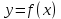 «сжатием» к оси х в 2 раза. «сжатием» к оси х в 2 раза. 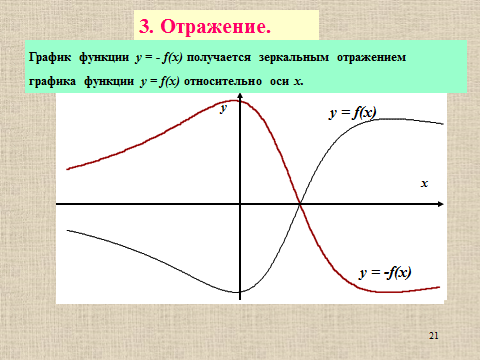 3. Отражение. График функции 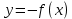 получается зеркальным отражением графика функции получается зеркальным отражением графика функции 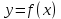 относительно оси х. относительно оси х. 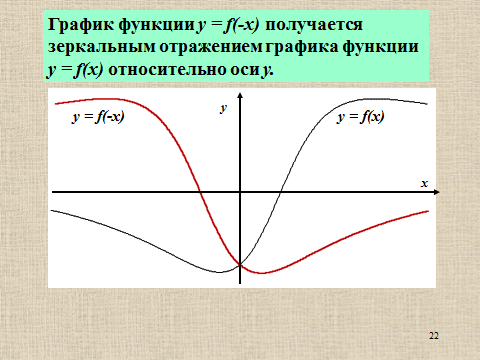 График функции 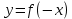 получается зеркальным отражением графика функции получается зеркальным отражением графика функции 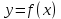 относительно оси у. относительно оси у. 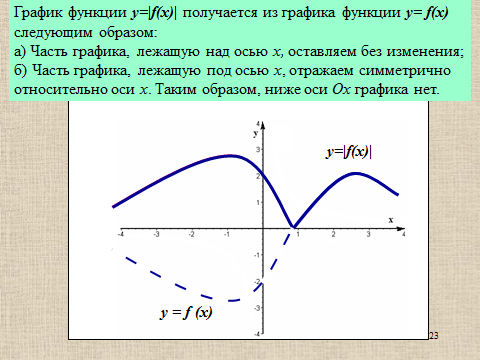 График функции 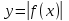 получается из графика функции получается из графика функции 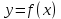 следующим образом: следующим образом: а) Часть графика, лежащую над осью x, оставляем без изменения; б) Часть графика, лежащую под осью x, отражаем симметрично относительно оси x. Таким образом, ниже оси Ox графика нет. 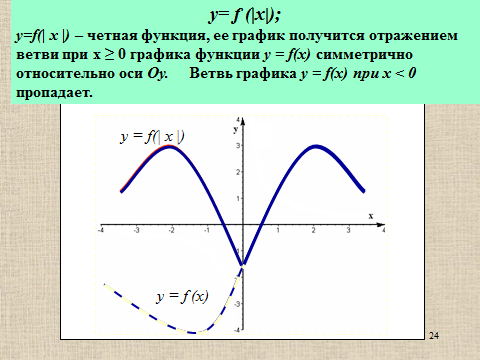 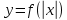 ; ; 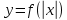 – четная функция, ее график получится отражением ветви при x≥0 графика функции – четная функция, ее график получится отражением ветви при x≥0 графика функции 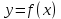 симметрично относительно оси Оу. Ветвь графика симметрично относительно оси Оу. Ветвь графика 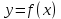 при х < 0 пропадает. при х < 0 пропадает.  Замечание. Нетрудно показать, что если 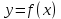 периодическая функция с периодом периодическая функция с периодом 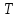 , то функция , то функция 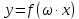 , , 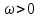 , является периодической с периодом. В самом деле, так как функция , является периодической с периодом. В самом деле, так как функция 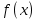 имеет период имеет период 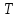 , то при любом x выполняется равенство , то при любом x выполняется равенство 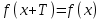 . Положим . Положим 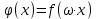 ; тогда для любого х получим ; тогда для любого х получим 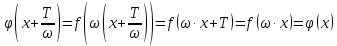 и, следовательно, функция 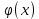 имеет период имеет период 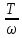 . Например, функция . Например, функция 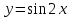 имеет период имеет период 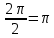 , а функция , а функция 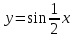 - период - период 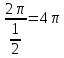 . . Список использованной литературы: 1. Бахтина Т. П. «Таблетки» и «компрессы» при построении графиков. // Математика в школе. 2000. № 8. 2. Игудисман О. С. Математика на устном экзамене. Пособие для поступающих в вузы с повышенными требованиями по математике. ─ М: «Московский Лицей», 1997. 3. Райхмист Р. Б. Графики функций: задачи и упражнения. ─ М: Школа-Пресс, 1997. - 384с. (Cерия «ШАНС» — «Школа Абитуриента: Научись Сам»). |
