Практическая работа №2. Построение таблиц истинности логических выражений

• Название: Построение таблиц истинности логических выражений
• Дата: 25.09.2022
• Размер: 18.24 Kb.
• Имя файла: Практическая работа №2.docx
• Тип: Практическая работа; #695863

Практическая работа №2

Тема: Построение таблиц истинности логических выражений.

Задание 1. Представить в виде таблицы виды логических операций:

Вид логической операции	Характеристика логической операции	Пример логической операции
1. Конъюнкция	Это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными.	A B A&B 0 0 0 0 1 0 1 0 0 1 1 1
2. Дизъюнкция	Это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выражения ложны.	A B A \/ B 0 0 0 0 1 1 1 0 1 1 1 1
3. Инверсия	Это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот.	A B ­A⸣ B⸣ 0 0 1 1 0 1 1 0 1 0 0 1 1 1 0 0
4.Эквивалентность	Это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.	A B AB 0 0 1 0 1 0 1 0 0 1 1 1
5. Импликация	Это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь.	A B A→B 0 0 1 0 1 1 1 0 0 1 1 1

Задание 2. Составить таблицу истинности для формулы A⸣ \/ B⸣:

А	В			\/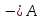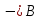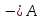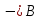
0	0	1	1	1
0	1	1	0	1
1	0	0	1	1
1	1	0	0	0

Задание 3. Заполнить таблицу и выполнить логические операции:

А	В	С	А \/ В	(А \/ В) \/ С
1	1	1	1	1
1	1	0	1	1
1	0	1	1	1
1	0	0	1	1
0	1	1	1	1
0	1	0	1	1
0	0	1	0	1
0	0	0	0	0

Задание 4. Заполнить таблицу и выполнить логические операции:

А	В	С	В \/ С	А /\ ( В \/ С)
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
1	0	0	0	0
1	1	0	1	1
0	1	1	1	0
1	0	1	1	1
1	1	1	1	1