|
|
Количественные и качественные характеристики надежности. Колличественные характеристики надежности. Построить графики зависимости P(t), a(t), . N
Задание
Рассчитать статистические оценки характеристик надёжности электронных модулей по результатам их испытаний: вероятность безотказной работы P*(t), частоту отказов a*(t), интенсивность отказов 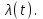 * и среднюю наработку до отказа Т*ср. Построить графики зависимости P*(t), a*(t), * и среднюю наработку до отказа Т*ср. Построить графики зависимости P*(t), a*(t), 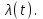 *. N0=1000 *. N0=1000
Исходные данные предоставлены в таблице 1.
Таблица 1
Вариант № 4
|
 t, час t, час
|
n( t) t)
|
|
 t, час t, час
|
n( t) t)
|
0-100
|
67
|
1500-1600
|
23
|
100-200
|
63
|
1600-1700
|
22
|
200-300
|
59
|
1700-1800
|
21
|
300-400
|
55
|
1800-1900
|
19
|
400-500
|
51
|
1900-2000
|
18
|
500-600
|
47
|
2000-2100
|
17
|
600-700
|
45
|
2100-2200
|
15
|
700-800
|
41
|
2200-2300
|
15
|
800-900
|
39
|
2300-2400
|
13
|
900-1000
|
36
|
2400-2500
|
13
|
1000-1100
|
33
|
2500-2600
|
11
|
1100-1200
|
32
|
2600-2700
|
12
|
1200-1300
|
29
|
2700-2800
|
10
|
1300-1400
|
27
|
2800-2900
|
9
|
1400-1500
|
26
|
2900-3000
|
9
|
Решение
Для выполнения работы необходимо использовать формулы статистических оценок надёжности.
Для определения величины вероятности безотказной работы P(t) используется следующая статистическая оценка

где N0- число изделий, поставленных на испытание или на эксплуатацию;
n(t) – число изделий, отказавших в течение времени t.
Для определения частоты отказов а(t) используется следующая статистическая оценка:
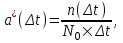
где n(Δt) –число отказавших изделий в интервале времени  . .
Статистическая оценка интенсивности отказов определяется:
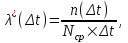
где Ncp – среднее число исправно работающих изделий в интервале времени  . .
Вероятность отказа Q*(t) определяется как:

1) Расчет величины вероятности безотказной работы P(t):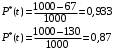
2) Расчет частоты отказов а(t):
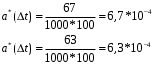
3) Статистическая оценка интенсивности отказов:

4) Расчёт вероятности отказа

Таблица 1 – Данные по отказам
 t, час t, час
|
n( ti) ti)
|
n(ti)
|
Q*(t),
|
P*(t),
|
a*( i),час-1 i),час-1
|
λ*( i), час-1 i), час-1
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
0…100
|
67
|
67
|
0,067
|
0,933
|
6,7*10-4
|
7,18*10-4
|
100…200
|
63
|
130
|
0,13
|
0,87
|
6,3*10-4
|
7,24*10-4
|
200…300
|
59
|
189
|
0,189
|
0,811
|
5,9*10-4
|
7,27*10-4
|
300…400
|
55
|
244
|
0,244
|
0,756
|
5,5*10-4
|
7,8*10-4
|
400…500
|
51
|
295
|
0,295
|
0,705
|
5,1 *10-4
|
7,23*10-4
|
500…600
|
47
|
342
|
0,342
|
0,658
|
4,7*10-4
|
7,14*10-4
|
600…700
|
45
|
387
|
0,387
|
0,613
|
4,5*10-4
|
7,34*10-4
|
700…800
|
41
|
428
|
0,428
|
0,572
|
4,1*10-4
|
7,17*10-4
|
800…900
|
39
|
467
|
0,467
|
0,533
|
3,9*10-4
|
7,32*10-4
|
900…1000
|
36
|
503
|
0,503
|
0,491
|
3,6*10-4
|
7,24*10-4
|
1000…1100
|
33
|
536
|
0,536
|
0,464
|
3,3*10-4
|
7,11*10-4
|
1100…1200
|
32
|
568
|
0,568
|
0,432
|
3,2*10-4
|
7,41*10-4
|
1200…1300
|
29
|
597
|
0,597
|
0,403
|
2,9*10-4
|
7,2*10-4
|
1300…1400
|
27
|
624
|
0,624
|
0,376
|
2,7*10-4
|
7,18*10-4
|
1400…1500
|
26
|
650
|
0,65
|
0,35
|
2,6*10-4
|
7,43*10-4
|
1500…1600
|
23
|
673
|
0,673
|
0,327
|
2,3*10-4
|
7,03*10-4
|
1600…1700
|
22
|
695
|
0,695
|
0,305
|
2,2*10-4
|
7,21*10-4
|
1700…1800
|
21
|
716
|
0,716
|
0,284
|
2,1*10-4
|
7,39*10-4
|
1800…1900
|
19
|
735
|
0,735
|
0,265
|
1,9*10-4
|
7,17*10-4
|
1900…2000
|
18
|
753
|
0,753
|
0,247
|
1,8*10-4
|
7,29*10-4
|
2000…2100
|
17
|
770
|
0,77
|
0,23
|
1,7*10-4
|
7,39*10-4
|
2100…2200
|
15
|
785
|
0,785
|
0,215
|
1,5*10-4
|
6,98*10-4
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
2200…2300
|
15
|
800
|
0,8
|
0,2
|
1,5*10-4
|
7,5*10-4
|
2300…2400
|
13
|
813
|
0,813
|
0,187
|
1,3*10-4
|
6,95*10-4
|
2400…2500
|
13
|
826
|
0,826
|
0,174
|
1,3*10-4
|
7,47*10-4
|
2500…2600
|
11
|
837
|
0,837
|
0,163
|
1,1*10-4
|
6,25*10-4
|
2600…2700
|
12
|
849
|
0,849
|
0,151
|
1,2*10-4
|
7,95*10-4
|
2700…2800
|
10
|
859
|
0,859
|
0,141
|
1*10-4
|
7,09*10-4
|
2800…2900
|
9
|
868
|
0,868
|
0,132
|
9*10-5
|
6,82*10-4
|
2900…3000
|
9
|
877
|
0,877
|
0,123
|
9*10-5
|
7,32*10-4
|
Построение графиков зависимости


 |
|
|
 Скачать 105.6 Kb.
Скачать 105.6 Kb. * и среднюю наработку до отказа Т*ср. Построить графики зависимости P*(t), a*(t),
* и среднюю наработку до отказа Т*ср. Построить графики зависимости P*(t), a*(t), 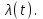 *. N0=1000
*. N0=1000
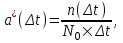
 .
.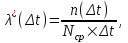
 .
.
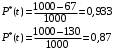
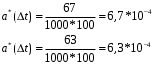






 t, час
t, час