общий+2011. Повышение эксплуатационной надежности электродвигателей находящиеся в эксплуатации агрофирмы кибрай диссертация магистра на получение степени магистра по

• Название: Повышение эксплуатационной надежности электродвигателей находящиеся в эксплуатации агрофирмы кибрай диссертация магистра на получение степени магистра по
• Дата: 29.05.2022
• Размер: 4.01 Mb.
• Имя файла: общий+2011.doc
• Тип: Диссертация; #556005
• страница: 3 из 6

Глава 2. Теоретические исследования процесса увлажнения изоляции обмоток электродвигателей
2.1. Преимущественные формы связи влаги с материалом изоляции электродвигателей.
Процесс переноса и удаления поглощенной диэлектриком влаги сопровождается нарушением связи с материалом. Согласно классификации академика А.Р. Ребиндера, формы связи влаги с материалом в зависимости от физико-химических свойств последнего делается на три больше группы: химическая связь, физико-химическая связь и физико-механическая связь.

К химической связи относится ионная и молекулярная связь. Физико-химическая связь образуется в результате молекулярного взаимодействия и характеризуется тремя формами связи: адсорбционная, осмотическая и структурная. Физико-механическая связь-это связь в микро и макрокапиллярах и связь смачивания.

В промышленности для изготовления изоляционных конструкций современных электродвигателей широко применяются синтетические полимеры, которые согласно классификации Ребиндере относится к капиллярно- пористым капиллярным телам. Для них характерна физико-химическая форма связи с влагой и физико-механическая связь смачивания. В слоистых пластиках и лакотканях преимущественной формой связи является физико-механическая связь влаги в макро и микрокапиллярах.

Адсорбционная связь влаги со скелетом изоляции обмоток электродвигателей характеризуется тем, что её формирование сопровождается значительным выделением теплоты, наибольшее количество которой выделяется при образовании первого молекулярного слоя. Ряд физических свойств адсорбционною- связанной воды; плотность, теплоёмкость, диэлектрическая проницаемость, вязкость, температура замерзания, объёмное сопротивление, давление насыщенного диэлектрика приводит к формированию новой дисперсной системы, обладающей упругими свойствами, характеризующим твёрдые тела.

Указанными свойствами обладает наиболее прочно связанный мономолекулярный слой влаги. Последующие слои удерживаются менее прочно, а их свойства по мере увеличения толщины слоя жидкости постепенно приближаются к свойствам свободной воды. Для удаления адсорбиционно – связанной влаги необходимо затратить энергию на отрыв её связи и на фазовое превращение воды в пар.

Капиллярная связь в зависимости от радиуса капилляра и длины свободного пробега молекул газа (l=10^-5см) делится на два вида- влага в макрокапиллярах, если средняя длина свободного пробега молекул l заничительно меньше радиуса капилляра  (l) <<1, влага в микрокапилллярах, если средняя длина свободного пробега больше радиуса капилляра (l/<1). Сущность такого деления на макро и микрокапилляры заключается в том, что механизм молекулярного переноса конденсированной влаги в этих капиллярах разный. В макрокапиллярах сорбция (а в микрокапиллярах перенос влаги происходит в виде эффузии) молекулярное течение, то есть активированная сорбция.

Физико-механическая связь смачивания в электроизоляционных материалах образуется путём непосредственного контакта диэлектрика с влажным воздухом. Причинами формирования этой связи являются поверхностное натяжение и сила тяжести. Количество влаги, удерживаемой диэлектриком в виде наружной плёнки, мало по сравнению с количеством влаги, находящейся внутри капиллярно – пористой структуры материала. Смоченный – изоляционный материал сохраняет свойства свободной води.

2.2. Оценка степени накопления конденсата в полости герметизированных неработающих электродвигателей
В сельскохозяйственном производство широко применяют электродвигатели закрытого исполнения, которое считается достаточным для предупреждения непосредственного проникновения влаги в обмотку. Однако, как показывает практика, полная герметизация здесь не достигается, так как электродвигатель “дышит”. Значительная часть этих электродвигателей установлена в неотапливаемых помещениях, под навесом или в помещениях с тяжелыми микроклиматическими условиями (животноводческие фермы) и на открытом воздухе, где изменения температуры и влажности более значительны и часты как на протяжении суток, так и сезона. При изменении температурного режима системы электродвигатель- окружающая среда влажный воздух через сальниковые уплотнения и отверстия для вводных проводов проникает во внутреннюю полость.

Рассмотрим процесс накопления влаги в полости электродвигателя. Электродвигатель закрытого исполнения можно рассматривать как открытую термодинамическую систему, обменивающуюся с окружающей средой теплотой и массой. Перед включением в работу система характеризуется следующими параметрами: постоянным объёмом, температурой и давлением внутри полости (Т_п и Т_п) равными температуре и давлению окружающей среды (Т_о.с. и Т_атм). При подаче напряжения на обмотку электродвигателя температура в полсти повышается. Рост температуры вызывает хаотическое тепловое движение молекул и атомов газовой смести, вследствие чего парциальное давление пара окружающей среды. Возникающие при этом градиенты температуры (∆Т) и давления (∆Р) обеспечивают вытеснение паров водя в окружающий воздух. По мере увеличения потока выходящего воздуха давление внутри электродвигателя постоянно снижается. При достижении установившегося значения температуры, давление в полости понижается до значения меньше атмосферного (Р_п<Р_атм).

При отключении электродвигателя и его постепенном охлаждении проникновению влажного воздуха в полость препятствует градиент температуры (Т), преобладающий над градиентом давления окружающей среды (Р). Перепад концентрации влаги на границе объектов обмотка – окружающая среда будет постоянным, до тех пор, пока температура не снизится до значения равновесия градиентов.

Время охлаждения (t) до температуры равновесия градиентов определяется по уравнению:

) (2.2.1)

Т_н – постоянная времени нагрева,

– рабочая температура обмотки,

_т – термоградиентный коэффициент переноса влаги,

U – градиент концентрации влаги.

При охлаждении обмоток электродвигателя ниже температуры равновесия во внутреннюю полость начинает проникать извне влажный воздух до тех пор, пока система не достигнет состояния термодинамического равновесия.

При резких колебаниях температуры окружающей среды во внутренней полости электродвигателя во время технологических пауз начинает накапливаться влага даже в неработающем электродвигателе.

При нагревании воздуха в окружающей среде выпадение влаги прекращается. Но влага, выпавшая ранее в конденсат в полости, выйти из полости обратно в окружающий воздух не может, так как для этого требуются затраты энергии, равные теплоте испарения этой внутриполостной влаги. При испарении влаги в окружающей среде увеличивается абсолютная влажность и соответственно возрастает парциальное давление газов и паров, образующих влажный воздух. Разность парциальных давлений в окружающей среде и в полости вызывает новый приток воздуха в оболочку электродвигателе, и повышение влагосодержания внутри его.

Количество влаги (G), накапливаемого в полости электродвигателя, подсчитывается по формуле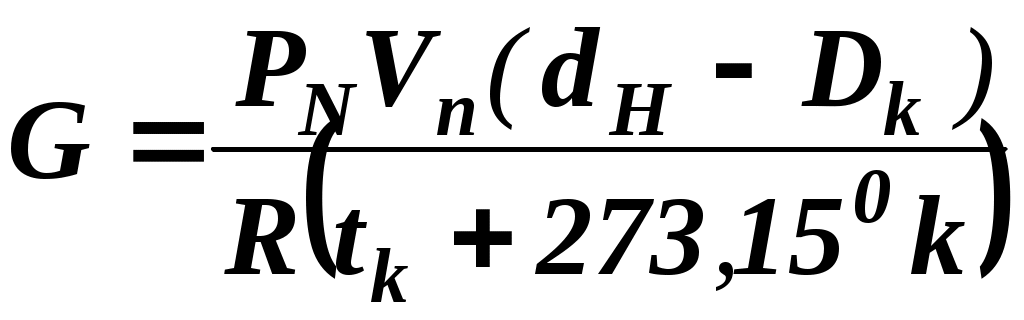

(2.2.2.)

где: Р_N – нормальное давление;

V_n –объём полости электродвигателя;

d_{H –} начальное влагосодержание;

d_k- конечное влагосодержание;

R –газовая постоянная;

t_k - конечная температура.

(2.2.3)

где: D – внутренний диаметр электродвигателя;

L – длина статора;

K – коэффициент объёма внутренней полости электродвигателя серии 4А.

(2.2.4)

где: Р _нас.н. – начальное давление насыщения,

W_Н – начальная относительная влажность.

(2.2.5)

где: Р_нас.к. – конечное давление насыщения.

По формуле (2.2.2) было рассчитано количество влаги, накапливаемой внутри электродвигателя серии 4А, мощности 160 кВт, с объемом полости под оболочкой 0,05 м³. Накопление конденсата в обмотках по массе составило 1,4 г за один день простоя при изменении дневной и ночной температур от +35⁰С до +10⁰С соответственно.
2.3. Процесс влагопоглощения в изоляции обмоток электродвигателя
Начальная стадия процесса поглощения изоляцией влаги из окружающего её влажного воздуха заключается в притяжении молекул водяного пара поверхностными молекулами диэлектрика. Этот процесс называется адсорбцией. Затем происходит диффузия паров воды в изоляцию, т.е. процесс адсорбции.

Характер процесса адсорбции влаги определяется с одной стороны свойствами такого сильно полярного диэлектрика, каким является вода, и с другой – свойствами материала изоляции, который как твёрдый диэлектрик обладает электрическим полем.

Молекулы водяного пара, являясь электрическими диполями, и осаждаясь на поверхности изоляции, под действием электрического поля притягиваются к точкам адсорбции диэлектрика своими положительно и отрицательно заряженными полюсами в зависимости от знака зарядов точек адсорбции, теряют их поверхность и принимают ориентированное положение. В результате поверхность первого мономолекулярного слоя влаги слагается из противоположных по знаку полюсов адсорбированных молекул, образующих новую совокупность точек адсорбции. Таким образом, формируется полимолекулярный слой, толщина которого тем больше, чем выше абсолютная влажность и температура воздуха. При изменении температуры от +5⁰ до +40⁰С, абсолютное содержание водяных паров в воздухе увеличатся от 6,8 г/м³ до 50,6 г/м³ соответственно.

Строение материала изоляции обмоток электродвигателей оказывает значительное влияние на процесс адсорбции паров воды диэлектриком его смачиваемость. Если материал имеет ионную структуру (лакоткань), адсорбция велика и очень слабо выражена, если изоляции состоит из неполярных или монополярных молекул (парафин). Степень адсорбции влаги зависит и от состава влажного воздуха. Если воздух содержит газы и соли, образующие ионы, (например в животноводческих помещениях, где концентрация аммиака достигает 0,03 г/м³, а углекислого газа 14,7 г/м³). При растворении ионов в парах воды процесс интенсифицируется, а также при самых минимальных значениях относительной влажности воздуха (10%) идёт формирование мономолекулярного слоя влаги на поверхность изоляции. Кроме того изоляция в молекулярном масштабе имеет шероховатую поверхность, на вершинах которых твёрдые частицы диэлектрика создают вокруг себя силовое поле с более высоким значением потенциала, результатом действия которого на дипольные молекулы влажного воздуха является образование у твёрдой поверхность материала изоляции ориентированного и прочно адсорбированного слоя связанной влаги.

Адсорбция влаги изоляцией обусловлена тем, что материалы, из которых изготовлены изоляционные конструкции электродвигателей различных серий и назначения – электрокартон, лакоткань, стеклолакоткань и др. характеризуются гигроскопичностью и пористостью. Средний радиус пор составляет для электрокартона – 300⁰ А, для лакткани – 100⁰ А, для стеклолакоткани – 70⁰А, что в несколько раз больше, чем диаметр молекулы воды – 2,7⁰А. Кроме того, под действием тепловых и механических нагрузок в изоляционном слое образуются трещины, сквозные щели и капилляры. Поэтому влага накапливаемая в полости электродвигателя в виде конденсата проникает в изоляцию, сначала в её лобовую часть, а потом под, влиянием разности влагосодержания, постепенно перемещается диффузионным путём к пазовой части обмотки, куда непосредственный доступ паров воды затруднён. Перенос поглощённой влаги в изоляции происходит, согласно, вследствие молярного перемещения паров воды материала по законам капиллярного движения (неактивированная сорбция) путём непосредственного внедрения молекул влаги между молекулами диэлектрика (активированная сорбция).

Не активированная сорбция влаги характерна для слоистых пластиков и лакотканей, эффективный радиус которых больше или соизмерим с радиусом молекула воды, а активированная форма сорбции преобладает у полимерных диэлектриков, размеры молекул которых в 10^-3 больше, чем молекулы влаги (2,7 *10^-9м).

Анионы, отталкиваясь от одноимённо зараженной поверхности, распределяются так, что их концентрация по мере удаления о поверхности постепенно повышается (см. рис. 2.2.а) Такое распределение ионов в диффузионной части Д.Э.С. полностью соответствует фундаментальному закону Больцмана - распределения заряженных частиц в электрическом поле, т.е.

(2.3.1)

где: n – концентрация рассматриваемых частиц в данной точке;

n₀ – концентрация частиц в той точке поля, где их потенциальная энергия W =0;

е – основание натуральных логарифмов;

- потенциальная энергия частиц;

КТ – энергия теплового движения.

Потенциальная энергия каждого иона равно соответственно

, ,

где: Z – валентность ионов с учётом знака заряда;

l – заряд электрона;

 - электрический потенциал, создаваемый ДЭС на расстоянии х от поверхности, существование которого связано с наличием у поверхности раздела фаз пространственно разделённых зарядов.

Распределение потенциала  в диффузионной части ДЭС определяется решением уравнения Пуассона

(2.3.2.)

где:  - объёмная плотность зарядов диффузионной части ДЭС.

_а – абсолютная диэлектрическая проницаемость дисперсионной среды в пределах ДЭС.

Если допустить, что дисперсионная среда (влага) является симметричным электролитом (валентности катионов Z₊ и анионов Z_- равны), тогда

(2.3.3)

Подставляя значения р в уравнение (2.3.2) и выражая п₊ и п_- в соответствии с законом Больцмана, получаем

(2.3.4)

Производя интегрирование с пределами, которые определяются из условия, что при х  0,  =₀ , т.е. вблизи поверхности раздела потенциал слоя равен потенциалу поверхности, после извлечения корня имеем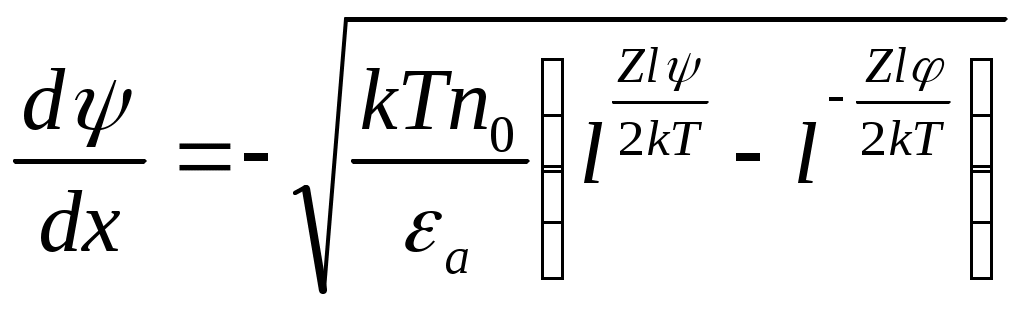

(2.3.5)

минус стоит пред корнем, так как при увеличении расстояния  - понтециала уменьшается.

В случае, когда в составе влажного воздуха концентрация заряженных частиц мала, поверхность изоляции слабо заряжается, тогда , экспоненты можно разложить в ряд Мак- Лорена, т.е.

и (2.3.6)

Подставляя эти значения в уравнение (2.3.5), получим

(2.3.7)

Если правую часть без  обозначить через N, то уравнение примет вид:

, (2.3.8)

После перестановки членов и в результате интегрирования в тех же пределах, имеем соотношение, определяшее изменение потенциала в ДЭС

или (2.3.9)

 потенциала неподвижного адсорбционного слоя.

В том случае, когда в составе влаги, накопленной внутри полости электрической машины или аппарата, имеется высокая концентрация ионов, что является характерным, например, для животноводческих помещений, где в составе влажного воздуха встречаются ионы аммиака, углекислого газа, соли и т.д. Тогда поверхность изоляции при обретает большой заряд , т.е. энергия притяжения противоионов к поверхности настолько превосходит энергию их теплового движения /КТ/, что противоионы «прилипают» к заряженной поверхности изоляции, образуя слой ионов с толщиной примерно равной размеру молекулы. В результате энергия притяжения ионов, находящихся в диффузной части ДЭС снижается. Таким образом а переделах адсорбционного слоя ионов потенциал понижается примерно по прямой до некоторой величины, называемой дзота- потенциал или электрокинетическим потенциалом. Далее в диффузионной части ДЭС меняется по экспоненциальному закону от S до 0 в соответствии с уравнением = Sе^-NX

Исходя, из вышеизложенной теории процессы предотвращения проникновения в изоляционную конструкцию электрических машин и аппаратов водяных паров и удаления абсорбированной ею влаги под действием электрического поля можно объяснить следующим образом. При приложении разности потенциалов (отрицательный полюс источника напряжения подключается к токоведущей части, а положительный к корпусу) имеет место смещение зарядов и появление электрических полюсов внутри диэлектрика. Это явление оказывает большое влияние на строение ДЭС и приводит к его деформации (см. рис.2.3. а,б.в,). Как видно из рисунка, отрицательно заряженные частицы отталкиваются от одноимённых зарядов, находящихся на границе между абсорбционным и диффузионным слоями, увеличивая их концентрацию и количество в диффузионной части ДЭС. Ионы диффузионного слоя, имеющие разные знаки, движутся в противоположных направлениях. Отрицательные ионы, в виду того, что их концентрация и подвижность преобладают над концентрацией и подвижностью положительных ионов, создают направленный поток избыточных ионов, который за счёт сил электрического притяжения, молекулярного сцепления и трения захватывает и увлекает за собой дипольные молекулы влаги, унося их в сторону положительного электрода (к корпусу).

В результате происходит перенос массы влаги со скоростью V и образуется некоторый градиент давления Р, возникающий при наличии сопротивления движению влаги.

Движение вязкой несжимаемой жидкости, какой является влага, под влиянием внешней силы (в нашем случае электрическое поле) и при наличии гидростатического давления можно описать с помощью гидродинамическое уравнение Навья-Стокса.

(2.3.10)

где: F_х –составляющая действующей на элемент объёма силы в направлении х,

– градиент давления;

 - коэффициент вязкости;

² – оператор Лапласа;

V – скорость переноса влаги.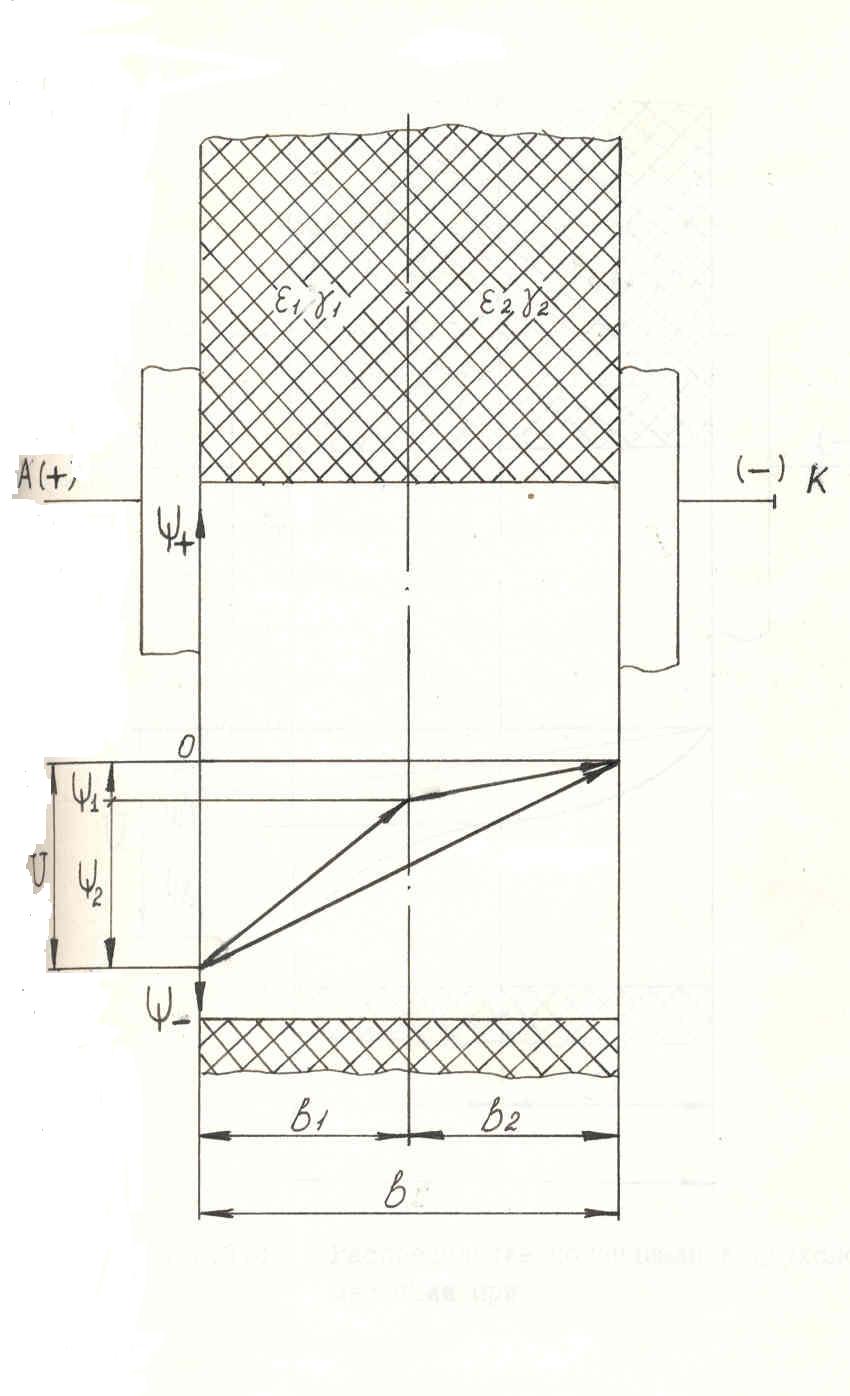


Рис. 2.3а. Распределение потенциала двухслойной изоляции при t = 0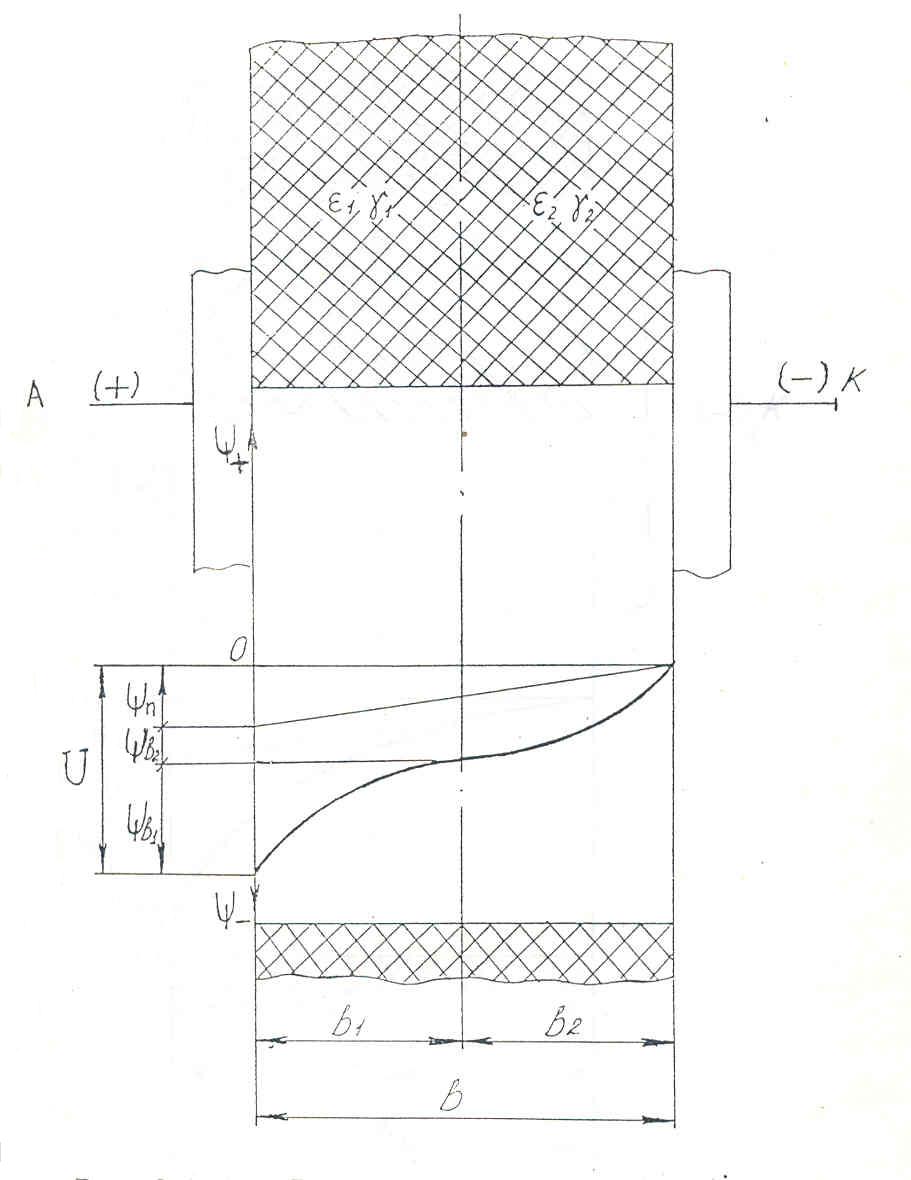



Рис. 2.3б. Распределение потенциала двухслойной изоляции при 0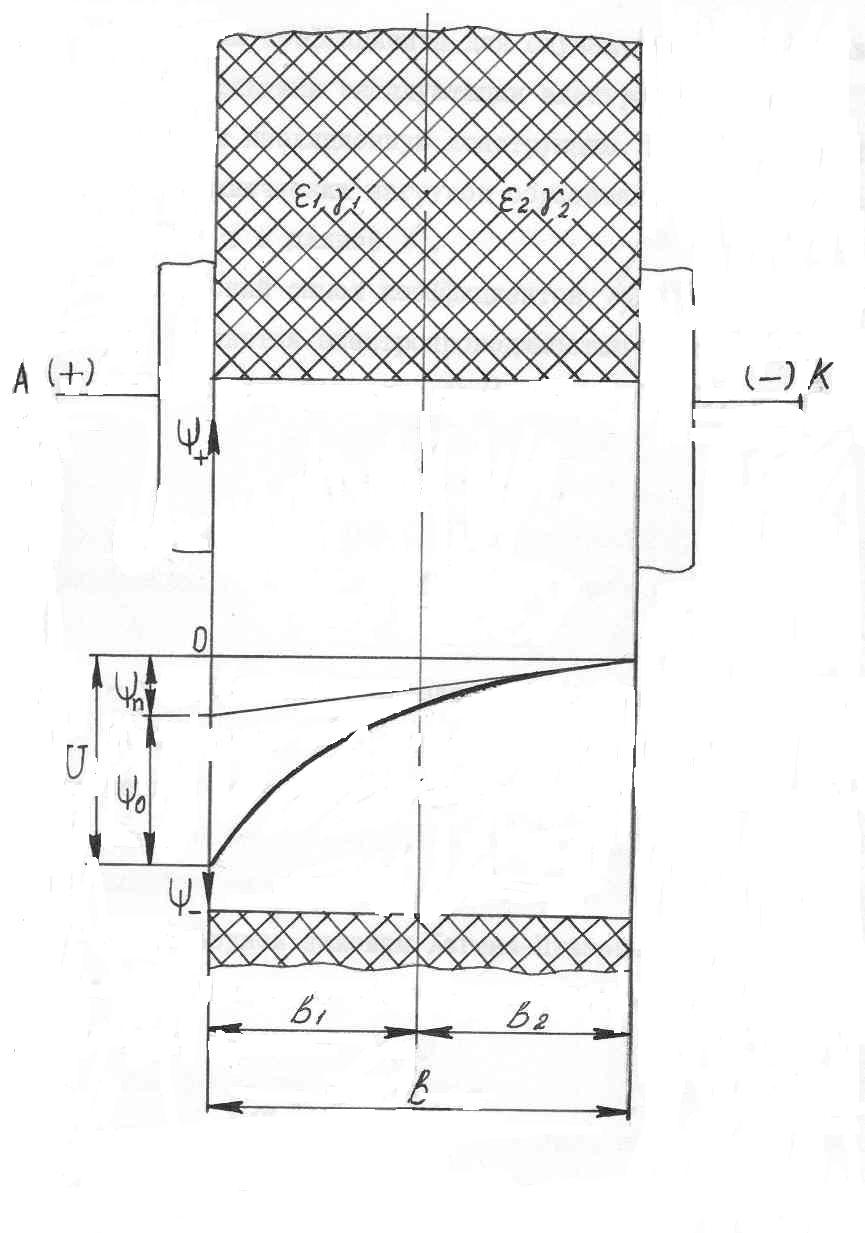


Рис. 2.3в. Распределение потенциала двухслойной изоляции при

Если принять, что электрическое поле Е линейно располагается в направлении , то

(2.3.11)

где: I – сила тока;

S – площадь сечения капилляра;

V – удельная электропроводность жидкости.

Действующая на единицу объёма влаги сила в направлении оси будет

(2.3.12)

где: – объёмная плотность заряда.

При условии ламинарного и стационарного течения жидкости (Р = const) имеем

(2.3.13)

Учитывая совместное воздействие внешнего Е и внутреннего Д.Э,С. электрических полей, воспользовавшись уравнением Пуассона

(2.3.14)

И подставляя (2.15) и (2.16) в (2.14), получим

(2.3.15)

где U – общий действующий на систему потенциал.

Если разложить скорость сечения на две составляющие гидростатическую V₁ и электрокниматическую V_II:

(2.3.16)

Можно записать

, (2.3.17) (2.3.18)

Общее решение этого уравнения даст

(2.3.19)

где – некоторая функция;

С – постоянная интегрирования.

По предпосылкам теории Гельмгольца (117), внешняя разность потенциалов накладывается на имеющееся внутри Д.Э.С. поле

Поэтому

(2.3.20)

где:  - скачок потенциала в Д.Э.С. Тогда

(2.3.21)

Так как V_II по уравнению (2.19) не зависит от , то

(2.3.22)

Из граничных условий V_II =0 и =₀,

где: ₀ – потенциал неподвижной адсорбционной части ДЭС следует, что

(2.3.23)

Сделав соответствующие подстановки в (2.19) получим

(2.3.24)

Приравниваем значение  - ₀ к электрикинетическому потенциалу S и находим, что

(2.3.25)

При отсутствии перепада гидростатического давления V₁= 0

(2.3.26)

Вводя объёмную скорость V₀= V*S, имеем

(2.3.27)

Из выражения (2.3.27) получим соотношение для определения электрокинетичского потенциала, широко применяемое на практике

(2.3.28)

Таким образом на основании вышеприведённого анализа процесса можно придти к следующему выводу. При наложении электрического поля, чем большое количество и концентрация отрицательных ионов в диффузионной части ДЭС другими словами, чем больше значение эффективного заряда и электрокинетического потенциала S, тем эффективнее результирующее воздействие движущего потока ионов на молекулы влаги и тем быстрее происходит процесс влага массопереноса в изоляционном материале. Причём со скоростью, пропорциональной произведению величины заряда на градиент потенциала.
2.4. Основные уравнения по массофизическому процессу переноса влаги в изоляционном материале
При исследовании и математическом описании процессов сушки и десорбции в изоляционных конструкциях современных электрических машин приходится анализировать процессы связанного тепло и массопереноса в капиллярно- порытых телах, механизм и закономерности которого подробно представлены в работах многих авторов.

Экспериментальные исследования показывают, что перенос влаги в капиллярно- пористых телах возникает не только из-за неоднородности влагосодержания, но и вследствие существование градиентов температуры (t), давления (Р), силового поля (градиент электрического потенциала ).

Общее уравнение переноса обычно записывается в следующей форме:

(2.5.1)

гед: - потенциал переноса;

V – скорость переноса;

q- поток переноса;

- объёмная плотность источников.

Для того, чтобы получить из общего уравнения переноса (2.5.1) уравнение, определяющее тот или иной процесс переноса, необходимо соответствующим образом определить и конкретизировать потенциалы переноса, плотности источников (теплоты, массы и электричества) и иметь информацию о величинах всех коэффициентов переноса. Однако, рассмотрение взаимосвязанных процессов тепло- и массопереноса на основе молекулярно-кинетической теории и теоретических представлений о структуре и свойствах изоляционных материалов и о характере связи влаги со скелетом изоляции в настоящее время является довольно сложной задачей. Вместе с тем эти процессы удовлетворительно могут быть описаны с помощью законов термодинамики необратимых процессов.

Из потенциальной теории тепломассопереноса известна система уравнений, описывающая случай, когда на перенос влаги, накопленной в изоляции, одновременно воздействуют потоки электричества q_e , массы q_м и тепла q_т

(2.5.2)

(2.5.3.)

(2.5.4)
Учитывая что при положении электрического поля процесс переноса влаги в изоляционном материале происходит без изменения температуры (изотермический процесс), т.е. Т =0, и учитывая что изоляция равномерно увлажнена по всему объёму С=0, систему уравнений (2.31) можно упростить и записать так:

(2.5.5.)

(2.5.6)

(2.5.7)

Исходя из линейных законов (2.5.6), и выражения взаимности (2.5.7) определим соотношения, с помощью которых можно найти три независимых коэффициента ₁₂= ₂₁, ₁₁ и ₂₂ характеризующих электрокиниматические явления в капиллярно – пористых телах
(2.5.8)

(2.5.9)
Определим коэффициенты для случая, имеющего очень важное значение для практики эксплуатации электрооборудования. Рассмотрим увлажнённую изоляционную конструкцию, внутри которой за счёт тепловых и механических нагрузок образовалась капиллярная трещина с радиусом r и длиной l.

Физический смысл коэффициентов к₁₁ и к₂₂ следующий. Коэффициент к₁₁ является электропроводимостью влаги в капилляре. При отсутствии разности давления (Р=0) из (2.5.9)

(2.5.10)

Для капилляра

(2.5.11)

где: v – удельная электропроводимость жидкости (влаги).

Коэффициент к₂₂ является гидродинамической проводимостью. При отсутствии разности электрического потенциала ( =0) из (2.33.) имеем

(2.5.12)

Воспользуясь законом Хагена-Пуазейля, описывающим скорость движения жидкости через капилляр, определим поток переносимой массы влаги через изоляцию. q_m.

(2.5.13)

где:  - коэффицент вязкости.

Таким образом, сравнивая уравнение (2.5.12) с уравнением (2.5.13) , получаем независимый коэффицент к₂₂

(2.5.14)

Для определения коэффицентов ₁₂ = ₂₁, физический смысл которых выражает эффект перекрещивания, используем теорию Гельмгольца об электрокинетических явлениях, предполагающую ДЭС – подобный плоскому конденсатору. Следовательно, при приложении разности потенциалов заряды, находящиеся на поверхности изоляции, перераспределяются. Тогда выражение для определения объёмного потока массы при отсутствии гидростатического давления будет иметь вид.

(2.5.15)

Сравнивая уравнения (2.5.14) и (2.5.15), получим выражение для определения независимого коэффицента к₂₁:
(2.5.16)

Согласно соотношению взаимности имеем:

(2.5.17)

Подставляя значения коэффицентов ₁₁, ₁₂ = ₂₁ и ₂₂ в (3.32), получим систему уравнений, описывающих при положении электрического поля.

(2.5.18)

(2.5.19)

Зная величины параметров l, r, , ,_a, S и определяя матрицу к системы уравнений (2.44) , можно судить об эффективности процесса переноса влаги в изоляции. Положительности детерминанта Д является условием существования электрокинетического потенциала S, без которого процесс извлечения адсорбционной изоляцией влаги не происходит где.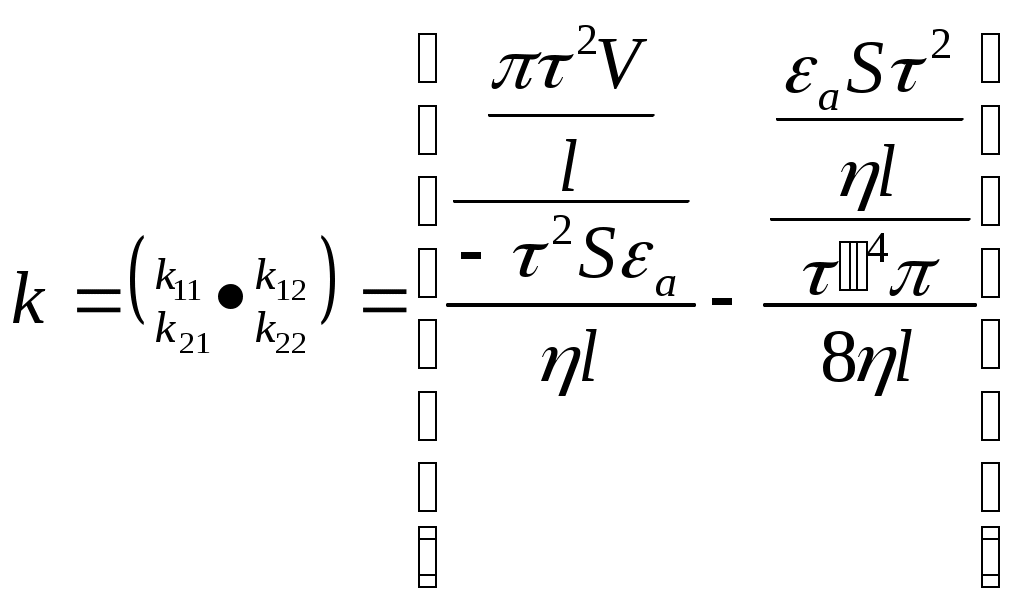

(2.5.20)

Тогда

(2.5.21)
Механизм влагопереноса в электроизоляционном материале под действием электрического поля тесно связан с понятием двойного электрического слоя (ДЭС), возникающего на границе раздела твёрдой (изоляция) и жидкой (влага) фаз. Образование ДЭС обусловлено конденсацией влажного воздуха на поверхности изоляции и существованием в его разноимённых заряженных частиц (ионы, дипольные молекулы воды, аэроны, электроны металлов, аэрозольные частицы и т.д.), которые ориентируются на границе раздела фаз. Заряженные частицы, примыкающие к поверхности изоляции, образуют адсорбционный слой ионов одного знака, прочно связанный с поверхностью твёрдой фазы, который нейтрализуется противоионами жидкой фазы, образующими компенсирующий неподвижный слой. Формирований компенсирующий слоя – противоинов осуществляется за счет сил электростатичкого притяжения к поверхностному заряду, т.е. носит физический характер. Более отдалённые от поверхности ионы, в отличие от первых, распределяются диффузионное у поверхности и подвижно с ней связаны.

По исследованиям (115) установлено, что поверхность вещества с более высокой абсолютной диэлектрической проницаемостью (_а) заряжается положительно, если оно контактирует с другим веществом, имеющим низкую абсолютную диэлектрическую проницаемость. Причём поверхность последнего заряжается отрицательно (_аН20>>_{а.изоляции})

Таким образом, у отрицательно заряженной поверхности изоляции скапливаются притягивающиеся к ней катионы. При удалении от поверхности их концентрация монотонно убывает.
2.5. Анализ процесса распределения потенциала в увлажённой изоляции под действием электростатического поля.
В соответствии с вышеприведённой теорией влагопереноса под действием электрического поля, в начальный момент при включении напряжения, заряженные частицы диффузионного слоя не перемещаются. Происходит лишь поляризация диэлектрика. Далее образуется поток ионов, создающий неравномерность их концентрации в ДЭС А через некоторый промежуток времени, при стабилизации процесса, наблюдается преимущественное движение отрицательных ионов в направлении положительного электрода, что приводит к извлечению водяных паров из изоляции.

Таким образом можно считать, что процесс состоит из двух режимов: переходного и установившегося, в каждом из которых потенциал неодинаково распределяется по объёму увлажнённой изоляции.

При анализе можно предположить, что неоднородная двухслойная увлажнённая изоляция находится между одинаковыми параллельными электродами (конденсатор), а сквозные щели (капилляры) располагаются прямолинейно и перпендикулярно плоскости электродов.

Рассмотрим следующие случаи распределения потенциала в изоляционном материале; в момент после наложения поля, в промежуточный и конечный моменты, до выключения приложенного напряжения.

При подключении системы на постоянное напряжение U, т.е. при переходном режиме (t=0), потенциал в первом (₁) и во втором (₂) слоях определяется по выражением.

, (2.6.1) (2.6.2)

где в₁и в₂ – толщина, а ₁ и ₂ – диэлектрическая проницаемость первого и второго слоёв соответственно.

При этом потенциал в капилляре распределяется согласно уравнению Лапласа

(2.6.3)

Решение, которого имеет вид

(2.6.4)

где А и А₁ – постоянные, представляющие собой поток, создаваемый электрическим полем, необходимым для удаления ионов диффузионного слоя и поток, образованный объёмным зарядом р_с связанных граничных условиях:

=0, =0, =в,  =U,

Получим

А₁=0, (2.6.5)

где q- заряд электрода;

S- площадь поперечного сечения рассматриваемого капилляра;

в - длина капилляра, (в=в₁ +в₂)

U – приложенное напряжение;

_{a -} диэлектрическая проницаемость системы:

Подставляя (2,48) в (2.47) получим соотношение

(2.6.6)

из которого видно, что потенциал, в начале процесса распередяется линейно.

Рассмотрим промежуточный случай, имеющий место спустя некоторое время после подачи постоянного напряжения U. Выражения, описывающие изменение потенциала в первом и во втором слоях изоляции во времени t, можно записать следующим образом (52)

(2.6.7)

(2.6.8)

где:  - постоянная времени, которая определяется по формуле:

(2.6.9)

Параллельно с этим процессом в капилляре происходит процесс извлечения адсорбированной влаги под действием сил электростатического поля. Таким образом в области ₂= + ₁ будет избыток отрицательных ионов, которые перемещаются в направлении положительного электрода, а на участке в₁ концентрация положительных ионов увеличивается. В этом случае приложенное внешнее напряжение уравновешивается с общей внутренней разница потенциалов. И тогда имеем

(2.6.10)

где: - потенциал поляризации; (2.6.11)

-потенциал в области ₁, созданный положительными ионами относительно катода; (2.6.12)

-потенциал в области ₂, созданный отрицательными ионами относительно анода. (2.6.13)

Здесь: _п - плотность поляризованного заряда;

₁ – плотность объёмного заряда в области в<sub>1

2</sub> – плотность объёмного заряда в области в₂

С учётом (2,58) для данного случая окончательно получим:

(2.6.14)

В конечный момент времени, до отключения напряжения (крайний случай), т.е. при t= на границе раздела между слоями диэлектрика скапливаются свободные заряды и плотности токов в первом (j₁) и втором (j₂) слоях становятся равными (j₁ = j₂). Тогда разность потенциалов в изоляционном материале определяется из следующих выражений.

, (2.6.15) (2.6.16)

Вместе с тем, в увлажнённой части изоляции (в капилляре) отрицательные ионы диффузионного слоя собираются вблизи анода, в результате чего в Д.Э.С. остаются только связанные ионы с равномерно распределённым зарядом. При этом распределение потенциала определяется согласно решению уравнения Пуассона.

(2.6.17)

где р – плотность объёмного заряда:

При =const, решение (2.51) принимает вид.

(2.6.18)

Для капилляра имеем

(2.6.19) (2.6.20)

где: _с – объёмный заряд связанных ионов;

₀ – объёмный заряд отрицательных ионов.

Тогда в соответствии с (2.52) и (2.53) получим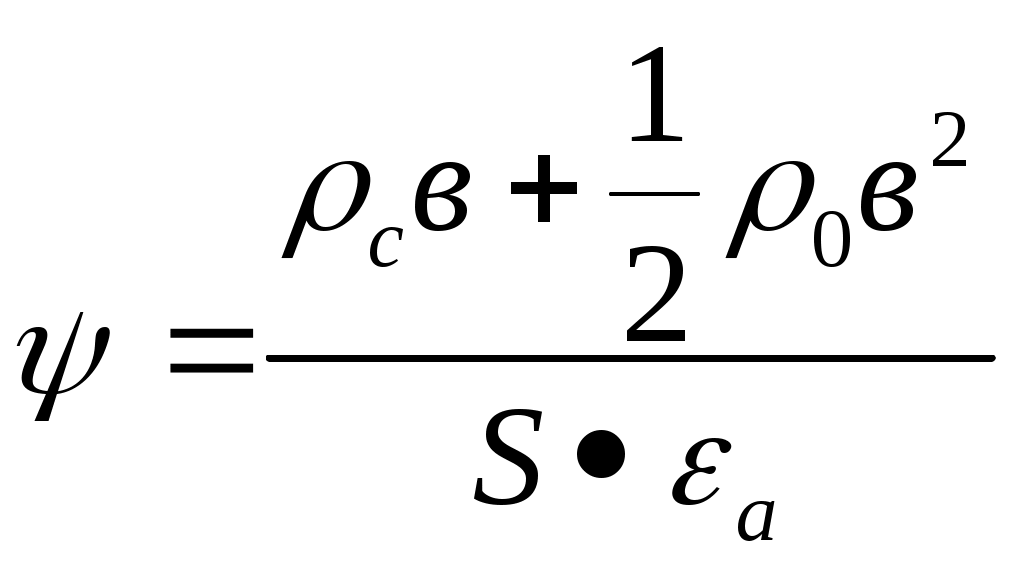

или (2.6.21)

где _п – потенциал поляризации двухслойной изоляции;

_о – потенциал на участке отрицательных ионов.

Следовательно в конечный период процесса влагопереноса распределение потенциала подчиняется закону параболы.

В результате можно прийти к следующим выводам:

1. Приложенное электростатическое поле меняется во времени внутри увлажённого изоляционного материла. Различные фазы распределения потенциала представлены ан рис.

2. Поляризация увлажённого диэлектрика отрицательно влияет на процесс переноса влаги из изоляции, уменьшая значения приложенного напряжения к системе и, следовательно, на эффективность воздействия электростатического поля.

Во избежание отмеченного явления следует использовать пульсирующее напряжение с отрицательным полупериодом, например промышленной частоты. Экспериментальные исследования (глава 3) подтвердят полученные теоретические результаты.