экзамен_10_математика. экзамен_10_матем_21. Пояснительная записка к экзаменационному материалу по математике для учащихся 10 класса
 Скачать 72.46 Kb.
|
|
Пояснительная записка к экзаменационному материалу по математике для учащихся 10 класса. Цель экзамена: проверка уровня предметной компетентности учащихся 10 класса по математике за курс 10 класса в рамках проведения промежуточной аттестации. Требования, предъявляемые к знаниям и умениям учащихся на экзамене: - знать основные тригонометрические формулы, и уметь применять их для преобразования выражений; - находить значение тригонометрических функций по известному значению одной из них; - знать формулы корней тригонометрических уравнений и уметь применять их для решения тригонометрических уравнений; - уметь решать показательные уравнения; - знать взаимное расположение прямых и плоскостей в пространстве; - уметь вычислять значение выражения с корнями, - уметь находить площадь поверхности в многогранниках. Форма экзамена: письменно, по контрольно-измерительным материалам. Количество вариантов - 2. Время выполнения экзаменационной работы: 90 минут Структура экзаменационной работы: Каждый вариант экзаменационной работы содержит 2 части. 1 часть содержит 5 заданий по алгебре и началам анализа и 1 задание по геометрии базового уровня сложности. Эти задания направлены на проверку усвоения основных свойств, понятий, владения основными алгоритмами, умения решать простейшие уравнения. 2 часть содержит 1 задание по алгебре и началам анализа и 1 задание по геометрии повышенного и высокого уровня сложности. При выполнении этих заданий проверяется умение учащихся применять знания в несколько измененной ситуации. В заданиях второй части учащиеся должны записать решения и обосновать их. Ответы к промежуточной аттестации по математике за курс 10 класса
Критерии оценивания работы: Каждое задание 1 части оценивается в один балл, задания 2 части оцениваются в 2 балла.
/ Промежуточная аттестация по математике за курс 10 класса. Вариант 1. А1. Вычислите значение выражения  .А2. . По заданной формуле вычислите первые пять членов последовательности (уn): yn=2n2-n. А3. Вычислите sin 210º + tg 2250. А4. Найдите корень уравнения cos t= - 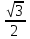 . А5. Точки А,В, С и Д не лежат в одной плоскости. Выберите верное утверждение: 1) прямая АВ параллельна прямой СД; 2) прямая АВ пересекает прямую СД; 3) прямая АС пересекает прямую ВД; 4) прямые АС и ВД – скрещиваются. В1. Найдите tgx, если cosx = 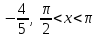 С1.а) Решите уравнение sin2х +2sin2 х =0. С2. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.  Промежуточная аттестация по математике за курс 10 класса. Вариант 2. А1. Вычислите значение выражения  .А2. По заданной формуле вычислите первые пять членов последовательности (уn): yn=  А3. Вычислите cos 120º+ tg 3150. А4. Найдите корень уравнения cos t= 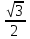.А5. Точки А,В, С и Д лежат в одной плоскости. Выберите утверждение, которое не может быть верным: 1) прямая АВ параллельна прямой СД; 2) прямая АВ пересекает прямую СД; 3) прямые АС и ВД – скрещиваются; 4) прямая АС пересекает прямую ВД. В1. Найдите tgx, если cos x = 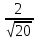 ,  С1.а) Решите уравнение 2sin2 х - 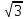 sin2х =0.С2. В правильной треугольной пирамиде SABCточка M– середина ребра AB, S – вершина. Известно, что BC=3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка SM.  Промежуточная аттестация по математике за курс 10 класса. Вариант 1. А1. Вычислите значение выражения .А2. . По заданной формуле вычислите первые пять членов последовательности (уn): yn=2n2-n. А3. Вычислите sin 210º + tg 2250. А4. Найдите корень уравнения cos t= - 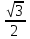. А5. Точки А,В, С и Д не лежат в одной плоскости. Выберите верное утверждение: 1) прямая АВ параллельна прямой СД; 2) прямая АВ пересекает прямую СД; 3) прямая АС пересекает прямую ВД; 4) прямые АС и ВД – скрещиваются. В1. Найдите tgx, если cosx = 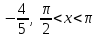С1.а) Решите уравнение sin2х +2sin2 х =0. С2. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4. Промежуточная аттестация по математике за курс 10 класса. Вариант 2. А1. Вычислите значение выражения .А2. По заданной формуле вычислите первые пять членов последовательности (уn): yn= А3. Вычислите cos 120º+ tg 3150. А4. Найдите корень уравнения cos t= 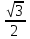.А5. Точки А,В, С и Д лежат в одной плоскости. Выберите утверждение, которое не может быть верным: 1) прямая АВ параллельна прямой СД; 2) прямая АВ пересекает прямую СД; 3) прямые АС и ВД – скрещиваются; 4) прямая АС пересекает прямую ВД. В1. Найдите tgx, если cos x = 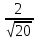,  С1.а) Решите уравнение 2sin2 х - 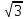sin2х =0.С2. В правильной треугольной пирамиде SABCточка M– середина ребра AB, S – вершина. Известно, что BC=3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка SM. |
, у4=1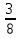
, у5=1,4
