ОЦЕНКА РАБОТОСПОСОБНОСТИ СИСТЕМ ТЯГОВОГО ЭЛЕКТРОСНАБЖЕНИЯ С УЧЕТОМ НАДЕЖНОСТИ ЕЕ ОСНОВНЫХ ЭЛЕМЕНТОВ. Пояснительная записка к курсовому проекту по дисциплине Основы теории надежности оценка работоспособности систем тягового электроснабжения с учетом надежности ее основных элементов
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
Определение доверительных интервалов для числовых оценок параметров надежности P(t), Q(t), f(t), λ(t)Таблица 6 – значение доверительной вероятности
Таблица 7 –функция Лапласа в зависимости от значений аргумента
Любое значение искомого параметра, вычисленное на основе ограниченного числа опытов, всегда будет содержать элемент случайности. Такое приближенное значение называется оценкой параметра. Вычисляется оценка 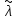 (среднее значение): (среднее значение):
где k – число значений случайной величины λ, k = 10. 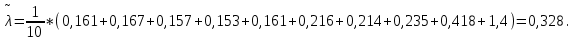 Определяется несмещенная оценка 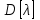 (дисперсия, вычисленная по опытным данным): (дисперсия, вычисленная по опытным данным):
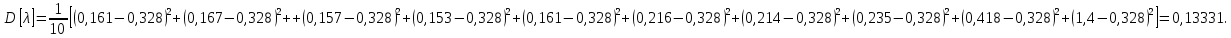 Дисперсия выборочной средней величины:
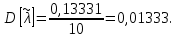 Определяется оценка σ (среднеквадратичное отклонение):
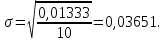 Определяется отклонение ε:
где – доверительная вероятность. 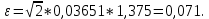 Определяются нижняя и верхняя доверительные границы:
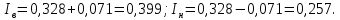 Определяется доверительный интервал
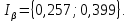 Вычисляется оценка 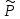 (среднее значение): (среднее значение):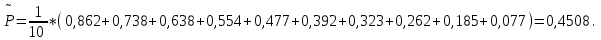 Определяется несмещенная оценка 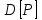 (дисперсия, вычисленная по опытным данным): (дисперсия, вычисленная по опытным данным):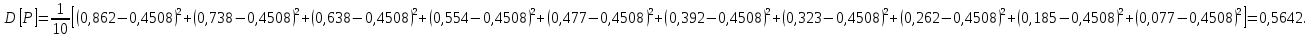 Дисперсия выборочной средней величины: 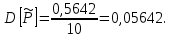 Определяется оценка σ (среднеквадратичное отклонение): 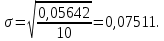 Определяется отклонение ε: 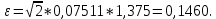 Определяются нижняя и верхняя доверительные границы: 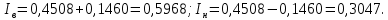 Определяется доверительный интервал 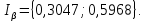 Вычисляется оценка 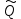 (среднее значение): (среднее значение):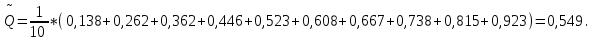 Определяется несмещенная оценка 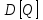 (дисперсия, вычисленная по опытным данным): (дисперсия, вычисленная по опытным данным):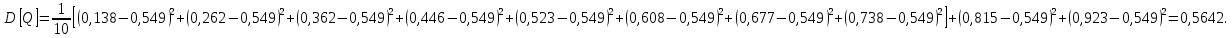 Дисперсия выборочной средней величины: 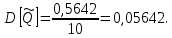 Определяется оценка σ (среднеквадратичное отклонение): 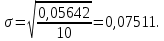 Определяется отклонение ε: 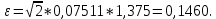 Определяются нижняя и верхняя доверительные границы: 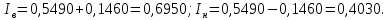 Определяется доверительный интервал 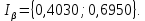 Полученные интервалы наносятся на графики, построенные в пункте 1. 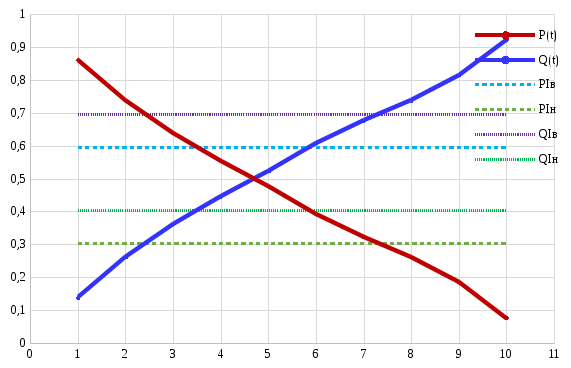 Рисунок 5 – зависимость вероятности безотказной работы элементов P(t) и её доверительный интервал (PIН;PIВ), зависимость вероятности отказа Q(t) от времени и её доверительный интервал (QIН;QIВ) 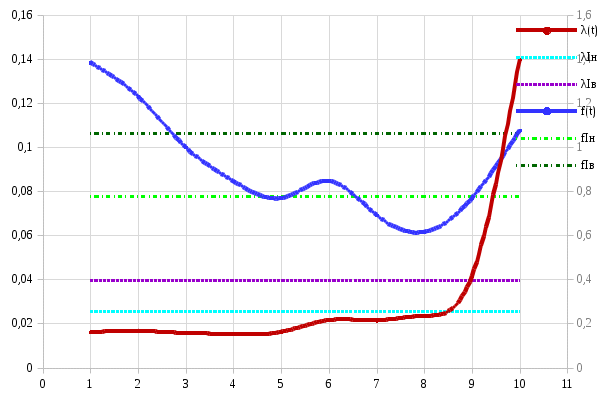 Рисунок 6 - зависимость вероятности безотказной работы элемента f(t) и её доверительный интервал (fIН;fIВ), зависимость интенсивности отказа λ(t) от времени и её доверительный интервал (λIН; λIВ) |

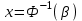
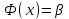
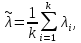
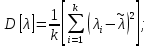
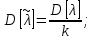
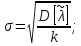
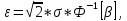
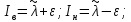
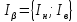 ;
;