Пояснительная записка к курсовому проекту по курсу "Механика горных пород и грунтов"
 Скачать 420.23 Kb. Скачать 420.23 Kb.
|
|
Таблица 6. Дополнительные напряжения и осадка фундамента в сечении Б-2
Относительная осадка фундамента равна 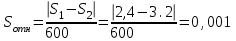 и не превышает предельную величину равную 0,002. и не превышает предельную величину равную 0,002.3. Проверка устойчивости запроектированной подпорной стенки и разработка рекомендаций по обеспечению ее устойчивости или снижение коэффициента устойчивости стенки 3.1 Расчет величины активного давления грунта на подпорную стенку Подпорная стенка принимается II класса с вертикальной задней гранью, жесткой, неподвижной, угол трения грунта о стенку 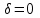 . Поверхность засыпки за подпорной стенкой – горизонтальная. За подпорной стенкой разрез двухслойный – это полутвердая глина и подстилающие ее пески мелки, плотные, маловлажные. Мощность глин за подпорной стенкой – 4,2 м.( . Поверхность засыпки за подпорной стенкой – горизонтальная. За подпорной стенкой разрез двухслойный – это полутвердая глина и подстилающие ее пески мелки, плотные, маловлажные. Мощность глин за подпорной стенкой – 4,2 м.(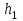 ), песков –1,8 м.( ), песков –1,8 м.(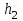 ). ).Глины обладают трением и сцеплением, поэтому интенсивность их давления на заднюю грань подпорной стенки определяется по формуле: 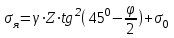 , ,где 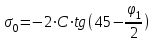 - это боковое давление, не оказывающее влияния на подпорную стенку из-за сил сцепления ( - это боковое давление, не оказывающее влияния на подпорную стенку из-за сил сцепления (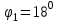 ). ).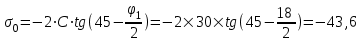 кПа кПаГлубина от верхней грани подпорной стенки, на которой последняя не испытывает давления со стороны грунта, определяется по формуле: 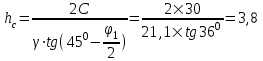 м м Определяем напряжение на уровне подошвы глин: 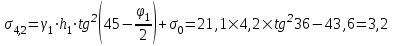 кПа кПаОпределяем напряжение на уровне кровли песка ( 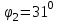 ). ).Для этого необходимо рассчитать 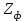 : :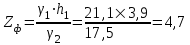 м м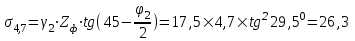 кПа кПаОпределяем напряжение на уровне подошвы подпорной стенки: 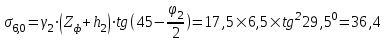 кПа кПаПолное активное давление грунта на подпорную стенку равно: 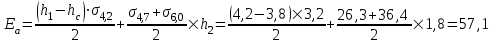 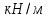 3.2 Проверка подпорной стенки на плоский сдвиг по грунту Для предотвращения скольжения подпорной стенки на уровне подошвы должно быть удовлетворено неравенство 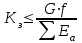
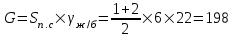 кН/м кН/м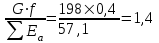 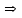 условие условие 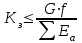 , , 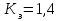 , выполняется, следовательно, подпорная стенка не будет подвержена плоскому сдвигу. , выполняется, следовательно, подпорная стенка не будет подвержена плоскому сдвигу.3.3 Проверка подпорной стенки на опрокидывание Отношение величины момента, удерживающего стенку от опрокидывания  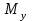 , к моменту, опрокидывающему ее , к моменту, опрокидывающему ее 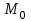 , называется коэффициентом устойчивости стены против опрокидывания , называется коэффициентом устойчивости стены против опрокидывания 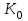 и должно быть не менее 1,5. и должно быть не менее 1,5. 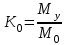 , , где  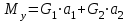 ; ; 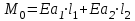 ; ;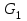 и и 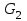 - веса блоков подпорной стенки длиной 1м, кН; - веса блоков подпорной стенки длиной 1м, кН;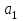 и и 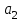 - расстояния от т. С до осей приложения сил - расстояния от т. С до осей приложения сил 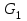 и и 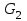 , равные соответственно 1,5 и 0,65 м; , равные соответственно 1,5 и 0,65 м;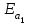 и и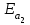 - величины распора грунтов на блок длиной 1м, равные соответственно 57,1 и 0,64 кН; - величины распора грунтов на блок длиной 1м, равные соответственно 57,1 и 0,64 кН;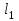 - расстояние от т. А до оси приложения - расстояние от т. А до оси приложения 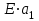 , определяемое как , определяемое как 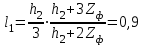 м.; м.;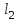 - расстояние от т. А до оси приложения - расстояние от т. А до оси приложения 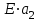 , определяемое как , определяемое как 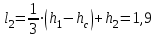 м. м.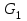 и и 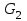 определяются по формулам: определяются по формулам: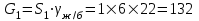 кН/м кН/м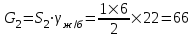 кН/м кН/м Вычислим значения моментов 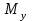 и и 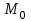 : :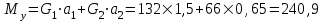 кН кН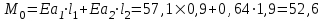 кН кН Определяем отношение величин моментов: 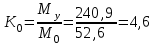 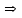 подпорная стенка устойчива против опрокидывания. подпорная стенка устойчива против опрокидывания.3.4 Разработка рекомендаций по снижению коэффициента устойчивости стенки Приведенные выше расчеты проверки подпорной стенки на опрокидывание и плоский сдвиг показали, что подпорная стенка устойчива, но коэффициент запаса больше необходимого. Из экономических соображений можно было бы облегчить стенку, уменьшив ее объем и сократив, таким образом, расход железобетона, Так же изменить коэффициент запаса можно за счет изменения веса бетона. Исходя из всех предложений, можно сделать вывод, что необходимо изменение конструкции подпорной стенки и составляющего ее материала. 4. Проверка устойчивости проектного откоса В практике проектирования наиболее часто используют при расчете устойчивости откосов метод круглоцилиндрической поверхности скольжения. Требуемый коэффициент запаса устойчивости откоса принимается для сооружений II класса, исходя из расчетной сейсмичности района равной или менее 7 баллов - 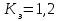 . В дальнейших расчетах все полученные значения коэффициента запаса будут сравниваться с . В дальнейших расчетах все полученные значения коэффициента запаса будут сравниваться с 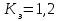 . .4.1 Проверка устойчивости откоса методом круглоцилиндрической поверхности скольжения Коэффициент устойчивости массива грунта в откосе вычисляется как отношение момента сил, удерживающих массив, к моменту сил, сдвигающих его. Проверка устойчивости откоса сводится к простейшему построению и расчетам. Из некоторого центра 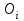 радиуса R проводят часть окружности; в плоскости чертежа она является следом поверхности, для которой проверяется возможность смещения массива грунта. Графически, по масштабу, определяем радиус кривой скольжения. Разбиваем массив на блоки, графически определяем их ширину и высоту сторон и производим расчет всех необходимых элементов для определения коэффициента устойчивости. радиуса R проводят часть окружности; в плоскости чертежа она является следом поверхности, для которой проверяется возможность смещения массива грунта. Графически, по масштабу, определяем радиус кривой скольжения. Разбиваем массив на блоки, графически определяем их ширину и высоту сторон и производим расчет всех необходимых элементов для определения коэффициента устойчивости. Так как массив грунта в откосе однородный и представлен полутвердыми глинами, коэффициент устойчивости определяется по формуле: 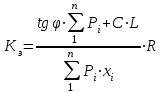 , ,
Длина дуги скольжения определяется по формуле: 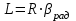 , ,где 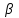 - это угол между линиями проведенными из центра О в точки основания и бровки откоса (начальная и конечная точки дуги скольжения) в радианах. - это угол между линиями проведенными из центра О в точки основания и бровки откоса (начальная и конечная точки дуги скольжения) в радианах. Основной трудностью является отыскание центра наиболее опасной дуги поверхности скольжения, которая определяется путем подбора. Если принять во внимание только сцепление, то этот центр окажется в точке пересечения двух прямых, точке О, одна из которых проведена от основания откоса под углом 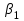 к поверхности откоса, а вторая от бровки откоса по углом к поверхности откоса, а вторая от бровки откоса по углом 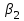 к горизонту. Величина к горизонту. Величина 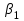 и и 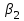 зависят от крутизны откоса высотой Н. зависят от крутизны откоса высотой Н.Значение 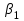 и и 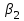 определяются исходя из значения определяются исходя из значения 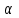 определяемого по формуле: определяемого по формуле: 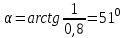 Зная 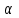 , по таблице 12 [1] определяем значения , по таблице 12 [1] определяем значения 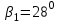 и и 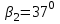 . Так как в таблице содержаться значения . Так как в таблице содержаться значения 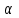 равные только 60, 45, равные только 60, 45, 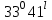 , , 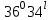 , , 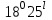 и и 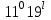 берем значения берем значения 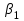 и и 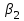 по значению по значению 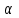 , к которому более близко наше расчетное значение , к которому более близко наше расчетное значение 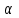 , т.е. , т.е. 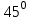 . .Чтобы учесть трение в грунте, нужно вниз от основания откоса отложить в масштабе величину высоты откоса Н и от полученной точки внутрь массива отложить расстояние, равное 4,5Н. Найденную таким образом точку Д соединить с точкой О. Центры наиболее опасных дуг скольжения, соответствующие разным значениям 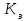 , будут располагаться на прямой ДО и ее продолжении. , будут располагаться на прямой ДО и ее продолжении.После проведения n-го количество расчетов 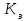 , в дальнейшем будут приведены вычисления только минимального, среднего и максимального значений , в дальнейшем будут приведены вычисления только минимального, среднего и максимального значений 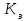 . .Максимальный коэффициент запаса достигается при значении 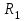 =14,4 м., =14,4 м., 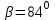 (1,48 радиан), L=21,3 м., число блоков равно 6, С=30 кПа, (1,48 радиан), L=21,3 м., число блоков равно 6, С=30 кПа, 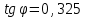 . .Данные расчетов приведены в таблице 7. Таблица 7. Расчеты по блокам
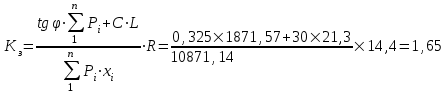 Минимальное значение коэффициента запаса достигается при значении 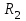 =16,5 м., =16,5 м., 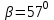 (1 радиан), L=16,5 м., число блоков равно 6, С=30 кПа, (1 радиан), L=16,5 м., число блоков равно 6, С=30 кПа, 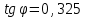 . Данные расчетов приведены в таблице 8. . Данные расчетов приведены в таблице 8.Таблица 8. Расчеты по блокам
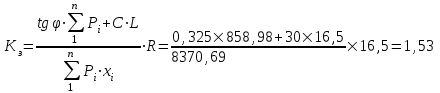 Промежуточное значение коэффициента запаса достигается при значении 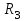 =17,1м., =17,1м., 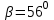 (0,98 радиан), L=16,8 м., число блоков равно 6, С=30 кПа, (0,98 радиан), L=16,8 м., число блоков равно 6, С=30 кПа, 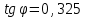 . Данные расчетов приведены в таблице 9. . Данные расчетов приведены в таблице 9.Таблица 9. Расчеты по блокам
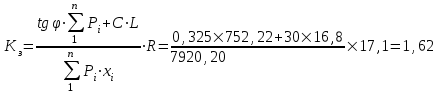 Вычисленные коэффициенты запаса показывают, что откос является устойчивым, так как минимальное его значение при заданных условиях не приближается и не является меньше допустимого значения 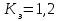 . Данная устойчивость откоса достигается за счет большого значения сцепления глинистых грунтов равного 30 кПа. . Данная устойчивость откоса достигается за счет большого значения сцепления глинистых грунтов равного 30 кПа.4.2 Построение профиля откоса по В.В. Соколовскому с использованием таблицы И.С. Мухина и А.И. Срагович В.В. Соколовский условно делит откос в грунтах, обладающих трением и сцеплением, на две зоны: верхний слой грунта, ограниченный вертикальной частью откоса и положительной полуосью y – зона упругого состояния, и массив грунта, расположенный ниже оси y – зона предельно напряженном состоянии. Максимально возможная высота вертикальной части откоса, представленного полутвердыми глинами, определяется по формуле: 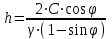 , ,где 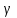 - удельный вес грунта, 21,1 - удельный вес грунта, 21,1  ; ;С – сцепление, 30 кПа; 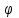 - угол внутреннего трения, - угол внутреннего трения, 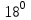 ; ;h – максимальная высота вертикальной части откоса, м. Определяем максимально возможную высоту вертикальной части откоса: 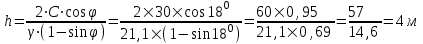 Приближенное определение координат точек, лежащих на поверхности устойчивого откоса в зоне предельно напряженного состояния, предложили И.С. Мухина и А.И. Срагович. Они составили таблицу для облегчения вычислений, которая приводится с некоторыми сокращениями, табл. 13[1]. Очертания равноустойчивого откоса от точки 0 и ниже по координатам, вычисляемым по формулам: 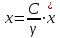 и и 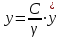 Расчет координат очертания откоса при коэффициенте устойчивости 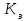 >1(в нашем случае >1(в нашем случае 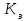 =1,2) в теории предельного равновесия производится по значениям: =1,2) в теории предельного равновесия производится по значениям: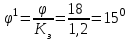 и и 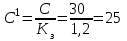 кПа кПаРезультаты расчетов координат очертания откоса приведены в таблице 10. Таблица 10. Координаты очертания откоса
Список использованной литературы Методические указания и задания для разработки курсового проекта по курсу «Механика горных пород и грунтов». Московский геологоразведочный институт; сост. А.А. Полуботко, В.В. Пендин. М., 1992 Цытович Н.А. Механика грунтов: Высш. шк., 1983 Полуботко А.А., Пендин В.В., Задачник по механике грунтов, Москва, 1991 г |

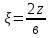
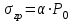 кПа
кПа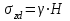 кПа
кПа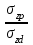
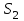 общая, см
общая, см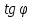 (для глинистых грунтов f=0,25, а для песков f=0,4). Принимаем f=0,4, так как глины не оказывают горизонтального давления на стенку).
(для глинистых грунтов f=0,25, а для песков f=0,4). Принимаем f=0,4, так как глины не оказывают горизонтального давления на стенку).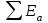 -
-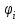 - угол внутреннего трения грунта, равный
- угол внутреннего трения грунта, равный 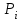 - вес расчетного блока, кН;
- вес расчетного блока, кН;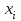 - плечо от линии действия центра тяжести блока до центра вращения, м;
- плечо от линии действия центра тяжести блока до центра вращения, м;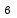 , м
, м