РЕФЕРАТ. Пояснительная записка содержит 127 страниц, 65 таблиц, 39 рисунков
 Скачать 7.41 Mb. Скачать 7.41 Mb.
|
ИССЛЕДОВАТЕЛЬСКАЯ ЧАСТЬ2.3.1. Оптимизация логической схемы БД3.3.1.1. Понятие «хорошей» схемы БД«Хорошая схема» базы данных – это схема БД, которая обладает следующими свойствами: 1) Свойство соединения без потерь: Если = (R1, R2,..., Rn) – схема БД, то для любого экземпляра = A = R1 U R2 U … U Rn, где А – объединение или множество атрибутов предметной области, имеет место следующее выражение: где 2) Свойство сохранения зависимости: Если = (R1, R2,..., Rn) – схема БД и F – множество функциональных зависимостей, то имеет место: где 3) Свойство нахождения в 3НФ. Любая схема отношения находится в третьей нормальной форме и при этом достигается:
4.3.1.2. Алгоритм построения «хорошей» схемы БДПусть R = (A1,…An) – универсальная схема отношений, F – множество функциональных зависимостей на R. Алгоритм.
Примечание: после выполнения п. 1-4 или 1-6 обладает свойством сохранения зависимости, и каждая схема отношения находится в 3НФ.
Схема БД = (поликлиника, отделение, врач, расписание, пациент, направление к врачу, анализ, направление на анализ, лаборатория, результат анализа, процедура, направление на процедуру, процедурный лист, лекарство, рецепт) множество отношений R. Таблица 3.1. Таблица «Поликлиника»
Таблица 3.2. Таблица «Отделение»
Таблица 3.3. Таблица «Врач»
Таблица 3.4. Таблица «Расписание»
Таблица 3.5. Таблица «Пациент»
Таблица 3.6. Таблица «Направление к врачу»
Таблица 3.7. Таблица «Анализ»
Таблица 3.8. Таблица «Направление на анализ» Таблица 3.9. Таблица «Лаборатория»
Таблица 3.10. Таблица «Результат анализа»
Таблица 3.11. Таблица «Процедура»
Таблица 3.12. Таблица «Направление на процедуру»
Таблица 3.13. Таблица «Процедурный лист»
Таблица 3.14. Таблица «Лекарство»
Таблица 3.15. Таблица «Рецепт»
Предметная область состоит из следующего числа атрибутов: R = (Pl1, Pl2, O1, O2, V1, V2, Rs1, Rs2, Pt1, Pt2, Nv1, Nv2, A1, A2, Na1, Na2, Lb1, Lb2, Ra1, Ra2, Pc1, Pc2, Np1, Np2, Pcl1, Pcl2, Lv1, Lv2, Rt1, Rt2) Формальные определения зависимостей, которые наблюдаются в предметной области, с учётом обозначений атрибутов сущностей: F = {Pl1 → Pl2, O1 → O2P1, V1 → V2O1, Rs1 → Rs2V1, Pt1 → Pt2, Nv1 → Nv2V1Pt1, A1 →A2, Na1 → Na2A1Lb1V1Pt1, Lb1 → Lb2, Ra1 → Ra2Na1Lb1, Pc1 → Pc2, Np1 → Np2Pc1Pt1V1, Pcl1 → Pcl2Np1, Lv1 → Lv2, Rt1 → Rt2Lv1V1Pt1} Для упрощения процесса вычисления отбросим из F все уникальные функциональные зависимости (в правой части которых нет ключей), получим: F = {O1 → P1, V1 → O1, Rs1 → V1, Nv1 → V1Pt1, Na1 → A1Lb1V1Pt1, Ra1 → Na1Lb1, Np1 → Pc1V1Pt1, Pcl1 → Np1, Rt1 → Lv1V1Pt1}
x→А0  (G - x→A0)+. Если принадлежит, то ее исключаем из множества G. (G - x→A0)+. Если принадлежит, то ее исключаем из множества G. Для того чтобы убедиться, входит ли зависимость x→А0  (G - x→A0)+ , достаточно построить замыкание множества функциональных зависимостей (G - x→A0)+. В этом случае, если А0 (G - x→A0)+ , достаточно построить замыкание множества функциональных зависимостей (G - x→A0)+. В этом случае, если А0  x+, то ее можно исключить из G. x+, то ее можно исключить из G.Минимизируем число атрибутов в правой части у каждой функциональной зависимости до 1, то есть каждую зависимость из F заменяем на совокупные, каждая из которых содержит один атрибут в правой части. G = {O1 → P1, V1 → O1, Rs1 → V1, Nv1 → V1, Nv1 → Pt1, Na1 → A1, Na1 → Lb1, Na1 → V1, Na1 → Pt1, Ra1 → Na1, Ra1 → Lb1, Np1 → Pc1, Np1 → V1, Np1 → Pt1, Pcl1 → Np1, Rt1 → Lv1, Rt1 → V1, Rt1 → Pt1}
G – O1 → P1 = {V1 → O1, Rs1 → V1, Nv1 → V1, Nv1 → Pt1, Na1 → A1, Na1 → Lb1, Na1 → V1, Na1 → Pt1, Ra1 → Na1, Ra1 → Lb1, Np1 → Pc1, Np1 → V1, Np1 → Pt1, Pcl1 → Np1, Rt1 → Lv1, Rt1 → V1, Rt1 → Pt1} Ol+ = Ol, P1  Ol+, O1 → P1 Ol+, O1 → P1 (G – O1 → P1)+ (G – O1 → P1)+Т.о. данную функциональную зависимость нельзя исключить.
G - V1 → O1 = {O1 → P1, Rs1 → V1, Nv1 → V1, Nv1 → Pt1, Na1 → A1, Na1 → Lb1, Na1 → V1, Na1 → Pt1, Ra1 → Na1, Ra1 → Lb1, Np1 → Pc1, Np1 → V1, Np1 → Pt1, Pcl1 → Np1, Rt1 → Lv1, Rt1 → V1, Rt1 → Pt1} V1+ = V1, O1  V1+, V1 → O1 V1+, V1 → O1 (G - V1 → O1)+ (G - V1 → O1)+Т.о. данную функциональную зависимость нельзя исключить.
G - Rs1 → V1 = {O1 → P1, V1 → O1, Nv1 → V1, Nv1 → Pt, Na1 → A1, Na1 → Lb1, Na1 → V1, Na1 → Pt1, Ra1 → Na1, Ra1 → Lb1, Np1 → Pc1, Np1 → V1, Np1 → Pt1, Pcl1 → Np1, Rt1 → Lv1, Rt1 → V1, Rt1 → Pt1} Rs1+ = Rs1, V1  Rs1+, Rs1 → V1 Rs1+, Rs1 → V1 (G - Rs1 → V1)+ (G - Rs1 → V1)+Т.о. данную функциональную зависимость нельзя исключить.
G - Nv1 → V1 = {O1 → P1, V1 → O1, Rs1 → V1, Nv1 → Pt1, Na1 → A1, Na1 → Lb1, Na1 → V1, Na1 → Pt1, Ra1 → Na1, Ra1 → Lb1, Np1 → Pc1, Np1 → V1, Np1 → Pt1, Pcl1 → Np1, Rt1 → Lv1, Rt1 → V1, Rt1 → Pt1} Nv1+ = Nv1Pt1, V1  Nv1+, Nv1 → V1 Nv1+, Nv1 → V1 (G - Nv1 → V1)+ (G - Nv1 → V1)+Т.о. данную функциональную зависимость нельзя исключить.
G - Nv1 → Pt1 = {O1 → P1, V1 → O1, Rs1 → V1, Nv1 → V1, Na1 → A1, Na1 → Lb1, Na1 → V1, Na1 → Pt1, Ra1 → Na1, Ra1 → Lb1, Np1 → Pc1, Np1 → V1, Np1 → Pt1, Pcl1 → Np1, Rt1 → Lv1, Rt1 → V1, Rt1 → Pt1} Nv1+ = V1O1P1, Pt1  Nv1+, Nv1 → Pt1 Nv1+, Nv1 → Pt1 (G - Nv1 → Pt1)+ (G - Nv1 → Pt1)+Т.о. данную функциональную зависимость нельзя исключить.
G - Na1 → A1 = {O1 → P1, V1 → O1, Rs1 → V1, Nv1 → V1, Nv1 → Pt1, Na1 → Lb1, Na1 → V1, Na1 → Pt1, Ra1 → Na1, Ra1 → Lb1, Np1 → Pc1, Np1 → V1, Np1 → Pt1, Pcl1 → Np1, Rt1 → Lv1, Rt1 → V1, Rt1 → Pt1} Na1+ = Na1Lb1V1O1P1Pt1, A1  Na1+, Na1 → A1 Na1+, Na1 → A1 ( G - Na1 → A1)+ ( G - Na1 → A1)+Т.о. данную функциональную зависимость нельзя исключить.
G - Na1 → Lb1 = {O1 → P1, V1 → O1, Rs1 → V1, Nv1 → V1, Nv1 → Pt1, Na1 → A1, Na1 → V1, Na1 → Pt1, Ra1 → Na1, Ra1 → Lb1, Np1 → Pc1, Np1 → V1, Np1 → Pt1, Pcl1 → Np1, Rt1 → Lv1, Rt1 → V1, Rt1 → Pt1} Na1+ = Na1V1Pt1O1P1A1, Lb1  Na1+, Na1 → Lb1 Na1+, Na1 → Lb1 ( G - Na1 → Lb1)+ ( G - Na1 → Lb1)+Т.о. данную функциональную зависимость нельзя исключить.
G - Na1 → V1 = {O1 → P1, V1 → O1, Rs1 → V1, Nv1 → V1, Nv1 → Pt1, Na1 → A1, Na1 → Lb1, Na1 → Pt1, Ra1 → Na1, Ra1 → Lb1, Np1 → Pc1, Np1 → V1, Np1 → Pt1, Pcl1 → Np1, Rt1 → Lv1, Rt1 → V1, Rt1 → Pt1} Na1+ = Na1Pt1A1, V1  Na1+, Na1 → V1 Na1+, Na1 → V1 ( G - Na1 → V1)+ ( G - Na1 → V1)+Т.о. данную функциональную зависимость нельзя исключить.
G - Na1 → Pt1= {O1 → P1, V1 → O1, Rs1 → V1, Nv1 → V1, Nv1 → Pt1, Na1 → A1, Na1 → Lb1, Na1 → V1, Ra1 → Na1, Ra1 → Lb1, Np1 → Pc1, Np1 → V1, Np1 → Pt1, Pcl1 → Np1, Rt1 → Lv1, Rt1 → V1, Rt1 → Pt1} Na1+ = Na1V1O1P1A1, Pt1  Na1+, Na1 → Pt1 Na1+, Na1 → Pt1 ( G - Na1 → Pt1)+ ( G - Na1 → Pt1)+Т.о. данную функциональную зависимость нельзя исключить.
G - Ra1 → Na1 = {O1 → P1, V1 → O1, Rs1 → V1, Nv1 → V1, Nv1 → Pt1, Na1 → A1, Na1 → Lb1, Na1 → V1, Na1 → Pt1, Ra1 → Lb1, Np1 → Pc1, Np1 → V1, Np1 → Pt1, Pcl1 → Np1, Rt1 → Lv1, Rt1 → V1, Rt1 → Pt1} Ra1+ = Ra1Lb1, Na1  Ra1+, Ra1 → Na1 Ra1+, Ra1 → Na1 ( G - Ra1 → Na1)+ ( G - Ra1 → Na1)+Т.о. данную функциональную зависимость нельзя исключить.
G - Ra1 → Lb1 = {O1 → P1, V1 → O1, Rs1 → V1, Nv1 → V1, Nv1 → Pt1, Na1 → A1, Na1 → Lb1, Na1 → V1, Na1 → Pt1, Ra1 → Na1, Np1 → Pc1, Np1 → V1, Np1 → Pt1, Pcl1 → Np1, Rt1 → Lv1, Rt1 → V1, Rt1 → Pt1} Ra1+ = Ra1Na1Pt1V1O1P1, Lb1  Ra1+, Ra1 → Lb1 Ra1+, Ra1 → Lb1 ( G - Ra1 → Lb1)+ ( G - Ra1 → Lb1)+Т.о. данную функциональную зависимость нельзя исключить.
G - Np1 → Pc1 = {O1 → P1, V1 → O1, Rs1 → V1, Nv1 → V1, Nv1 → Pt1, Na1 → A1, Na1 → Lb1, Na1 → V1, Na1 → Pt1, Ra1 → Na1, Ra1 → Lb1, Np1 → V1, Np1 → Pt1, Pcl1 → Np1, Rt1 → Lv1, Rt1 → V1, Rt1 → Pt1} Np1+ = Np1V1O1P1Pt1, Pc1  Np1+, Np1 → Pc1 Np1+, Np1 → Pc1 ( G - Np1 → Pc1)+ ( G - Np1 → Pc1)+Т.о. данную функциональную зависимость нельзя исключить.
G - Na1 → Ra1 = {O1 → P1, V1 → O1, Rs1 → V1, Nv1 → V1, Nv1 → Pt1, Na1 → A1, Na1 → Lb1, Na1 → V1, Na1 → Pt1, Ra1 → Na1, Ra1 → Lb1, Np1 → Pc1, Np1 → Pt1, Pcl1 → Np1, Rt1 → Lv1, Rt1 → V1, Rt1 → Pt1} Np1+ = Np1Pt1Pc1, V1  Np1+, Np1 → V1 Np1+, Np1 → V1 ( G - Np1 → V1)+ ( G - Np1 → V1)+Т.о. данную функциональную зависимость нельзя исключить.
G - Np1 → Pt1 = {O1 → P1, V1 → O1, Rs1 → V1, Nv1 → V1, Nv1 → Pt1, Na1 → A1, Na1 → Lb1, Na1 → V1, Na1 → Pt1, Ra1 → Na1, Ra1 → Lb1, Np1 → Pc1, Np1 → V1, Pcl1 → Np1, Rt1 → Lv1, Rt1 → V1, Rt1 → Pt1} Np1+ = Np1V1O1P1Pc1, Pt1  Np1+, Np1 → Pt1 Np1+, Np1 → Pt1 ( G - Np1 → Pt1)+ ( G - Np1 → Pt1)+Т.о. данную функциональную зависимость нельзя исключить.
G - Pcl1 → Np1 = {O1 → P1, V1 → O1, Rs1 → V1, Nv1 → V1, Nv1 → Pt1, Na1 → A1, Na1 → Lb1, Na1 → V1, Na1 → Pt1, Ra1 → Na1, Ra1 → Lb1, Np1 → Pc1, Np1 → V1, Np1 → Pt1, Rt1 → Lv1, Rt1 → V1, Rt1 → Pt1} Pcl1+ = Pcl1, Np1  Pcl1+, Pcl1 → Np1 Pcl1+, Pcl1 → Np1 ( G - Pcl1 → Np1)+ ( G - Pcl1 → Np1)+Т.о. данную функциональную зависимость нельзя исключить.
G - Rt1 → Lv1 = {O1 → P1, V1 → O1, Rs1 → V1, Nv1 → V1, Nv1 → Pt1, Na1 → A1, Na1 → Lb1, Na1 → V1, Na1 → Pt1, Ra1 → Na1, Ra1 → Lb1, Np1 → Pc1, Np1 → V1, Np1 → Pt1, Pcl1 → Np1, Rt1 → V1, Rt1 → Pt1} Rt1+ = Rt1V1O1P1Pt1 Lv1  Rt1+, Rt1 → Lv1 Rt1+, Rt1 → Lv1 ( G - Rt1 → Lv1)+ ( G - Rt1 → Lv1)+Т.о. данную функциональную зависимость нельзя исключить.
G - Rt1 → V1 = {O1 → P1, V1 → O1, Rs1 → V1, Nv1 → V1, Nv1 → Pt1, Na1 → A1, Na1 → Lb1, Na1 → V1, Na1 → Pt1, Ra1 → Na1, Ra1 → Lb1, Np1 → Pc1, Np1 → V1, Np1 → Pt1, Pcl1 → Np1, Rt1 → Lv1, Rt1 → Pt1} Rt1+ = Rt1Lv1Pt1, V1  Rt1+, Rt1 → Lv1 Rt1+, Rt1 → Lv1 ( G - Rt1 → Lv1)+ ( G - Rt1 → Lv1)+Т.о. данную функциональную зависимость нельзя исключить.
G - Rt1 → Pt1 = {O1 → P1, V1 → O1, Rs1 → V1, Nv1 → V1, Nv1 → Pt1, Na1 → A1, Na1 → Lb1, Na1 → V1, Na1 → Pt1, Ra1 → Na1, Ra1 → Lb1, Np1 → Pc1, Np1 → V1, Np1 → Pt1, Pcl1 → Np1, Rt1 → V1, Rt1 → V1} Rt1+ = Rt1Lv1V1O1P1, Pt1  Rt1+, Rt1 → Pt1 Rt1+, Rt1 → Pt1 ( G - Rt1 → Pt1)+ ( G - Rt1 → Pt1)+Т.о. данную функциональную зависимость нельзя исключить.
Если выполняется условие z→A  G+, то меняем содержимое G, то есть x →A заменяем на z→A. Тем самым выполняется операция попытки уменьшить число атрибутов в левой части функциональных зависимостей. G+, то меняем содержимое G, то есть x →A заменяем на z→A. Тем самым выполняется операция попытки уменьшить число атрибутов в левой части функциональных зависимостей.G = {O1 → P1, V1 → O1, Rs1 → V1, Nv1 → V1, Nv1 → Pt1, Na1 → A1, Na1 → Lb1, Na1 → V1, Na1 → Pt1, Ra1 → Na1, Ra1 → Lb1, Np1 → Pc1, Np1 → V1, Np1 → Pt1, Pcl1 → Np1, Rt1 → Lv1, Rt1 → V1, Rt1 → Pt1} В множестве G нет функциональных зависимостей с числом атрибутов больше одного в левой части, поэтому пропускаем этот пункт алгоритма и переходим к следующему.
G = {O1 → P1, V1 → O1, Rs1 → V1, Nv1 → V1Pt1, Na1 → A1Lb1V1Pt1, Ra1 → Na1Lb1, Np1 → Pc1V1Pt1, Pcl1 → Np1, Rt1 → Lv1V1Pt1}
Q = {P1P2, O1P1O2, V1O1V2, Pt1Pt2, Rs1V1Rs2, Nv1V1Pt1Nv2, Na1A1Lb1V1Pt1Na2, Ra1Na1Lb1Ra2, Np1Pc1V1Pt1Np2, Pcl1Np1Pcl2, Rt1Lv1V1Pt1Rt2, Lb1Lb2, Lv1Lv2, Pc1Pc2, A1A2}
Поскольку такой схемы P1O1P2V1O2Rs1Nv1Na1Np1Rt1V2Pt1Pt2A1A2Ra1Na2Lb1 Lb2Pc1Pcl1Pc2Lv1Rt1Lv2Rs2Nv2Ra2Np2Pcl2Rt2 нет, перейти к шагу 5.
После выполнения операции на этом шаге схема БД обладает свойством сохранения зависимостей, и каждая ее схема отношений находится в третьей нормальной форме. Таким образом, оптимальная схема БД совпадает с разработанной схемой БД, что и требовалось доказать. |

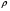 = 0 – множество схем отношений, которые образуют схему БД.
= 0 – множество схем отношений, которые образуют схему БД.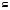 Q, то добавить в
Q, то добавить в 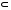 x), принадлежит ли z атрибуту A, то есть, принадлежит ли данная новая функциональная зависимость z→A множеству G+.
x), принадлежит ли z атрибуту A, то есть, принадлежит ли данная новая функциональная зависимость z→A множеству G+.