РГР по моделированию. ргр МиКМИД. Пояснительная записка содержит 23 листов, 2 рисунков, 3 таблиц, список использованных источников
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
 РЕФЕРАТ Пояснительная записка содержит 23 листов, 2 рисунков, 3 таблиц, список использованных источников. Цель работы – овладение графическим способом решения задач линейного программирования на примере расчета режимов резания для токарной обработки. При расчете режимов резания учитываются следующие ограничениями: • режущие возможности инструмента; • мощность электропривода главного движения станка; • заданная производительность станка на проектируемой операции; • наименьшая скорость резания, допускаемая кинематикой станка (наименьшая частота вращения шпинделя); • наибольшая технологически допустимая скорость резания; • наибольшая скорость резания, допускаемая кинематикой станка (наибольшая частота вращения шпинделя); • наибольшая подача, допускаемая кинематикой станка; • наибольшая подача, допускаемая требованиями, предъявляемыми к шероховатости обработанной поверхности. Содержание 1 Уравнения технических ограничений, характеризующие кинематику и динамику процесса резания металлов 4 1.1. Режущие возможности инструмента 4 1.2. Мощность электропривода главного движения станка 5 1.3. Заданная производительность станка на проектируемой операции 6 1.5. Наибольшая технологически допустимая скорость резания 10 1.6. Наибольшая скорость резания, допускаемая кинематикой станка 11 1.9 Наибольшая подача, допускаемая требованиями, предъявляемыми к шероховатости обработанной поверхности 12 2 Математическая модель процесса резания металлов 13 3 Выполнение расчета в MathCAD 18 Заключение 21 Список используемых источников 22 Приложение А – Листинг программы 23 Продолжение приложения А– Листинг программы 24 1 Уравнения технических ограничений, характеризующие кинематику и динамику процесса резания металлов1.1. Режущие возможности инструментаЭто ограничение устанавливает взаимосвязь между скоростью резания, обусловленной принятой стойкостью инструмента, материалом режущей части инструмента, его геометрией, глубиной резания, подачей, механическими свойствами обрабатываемого материала, с одной стороны, и скоростью резания, с другой стороны: 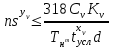 , (1) , (1)где 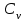 – постоянный коэффициент, характеризующий нормативные условия обработки; – постоянный коэффициент, характеризующий нормативные условия обработки;d–диаметр обрабатываемой детали или инструмента в мм; 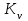 – общий поправочный коэффициент на скорость резания, учитывающий измененные условия обработки по сравнению с нормативными; – общий поправочный коэффициент на скорость резания, учитывающий измененные условия обработки по сравнению с нормативными;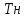 – принятая стойкость инструмента в мин; – принятая стойкость инструмента в мин;m – показатель относительной стойкости; 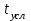 – глубина резания в мм; – глубина резания в мм;s – подача в мм/об (мм/мин); 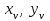 – показатели степеней соответственно при – показатели степеней соответственно при 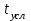 . .Состав общего поправочного коэффициента, учитывающего влияние различных факторов на скорость резания: 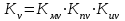 , где , где 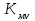 – поправочный коэффициент, учитывающий влияние физико-механических свойств обрабатываемого материала на скорость резания; – поправочный коэффициент, учитывающий влияние физико-механических свойств обрабатываемого материала на скорость резания; 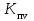 – поправочный коэффициент, учитывающий влияние поверхности заготовки на скорость резания – поправочный коэффициент, учитывающий влияние поверхности заготовки на скорость резания 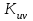 – поправочный коэффициент, учитывающий влияние инструментального материала на скорость резания. – поправочный коэффициент, учитывающий влияние инструментального материала на скорость резания.1.2. Мощность электропривода главного движения станкаЭто ограничение устанавливает взаимосвязь между эффективной мощностью, затрачиваемой на процесс резания, и мощностью электропривода главного движения станка: 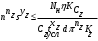 , (2) , (2)где 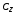 – постоянный коэффициент, характеризующий условия обработки; – постоянный коэффициент, характеризующий условия обработки;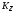 – общий поправочный коэффициент на мощность, учитывающий измененные условия обработки против нормативных; – общий поправочный коэффициент на мощность, учитывающий измененные условия обработки против нормативных;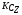 – коэффициент для приведения формулы к общему виду, равный – коэффициент для приведения формулы к общему виду, равный6120 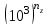 ; ;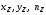 – показатели степеней, соответственно, при – показатели степеней, соответственно, при 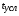 , s, , s,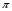 ; ;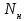 – мощность электродвигателя главного привода станка в квт; – мощность электродвигателя главного привода станка в квт; – коэффициент полезного действия механизма передачи от электродвигателя к инструменту. Примечание. Показатель степени 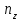 (1.2) равен (1.2) равен 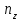 . .1.3. Заданная производительность станка на проектируемой операцииЭто ограничение учитывает взаимосвязь расчетных скорости резания и подачи с заданной производительностью станка: 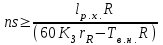 , (3) , (3)где 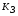 – коэффициент загрузки станка; – коэффициент загрузки станка;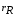 – число деталей, обрабатываемых одновременно на одной позиции; – число деталей, обрабатываемых одновременно на одной позиции;R – заданная производительность станка в шт/ч; 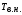 – сумма всех вспомогательных неперекрываемых времен при работе в мин; – сумма всех вспомогательных неперекрываемых времен при работе в мин;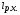 – длина рабочего хода инструмента в мм; – длина рабочего хода инструмента в мм;Среднее значение нормативного коэффициента загрузки оборудования по отделению или участку цеха при двухсменной работе следует принимать: для мелкосерийного производства 0,8…0,9; для серийного – 0,75…0,85; массового и крупносерийного – 0,65…0,75. Если на данном этапе тип производства еще неизвестен, то можно принять усредненные значения нормативного коэффициента загрузки оборудования порядка 0,75…0,8. Длина рабочего хода инструмента 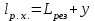 , где , где 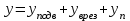 . .Сумма всех вспомогательных неперекрываемых времен при работе, состоит из затрат на отдельные приемы: 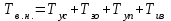 , ,где 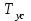 – время на установку и снятие детали, мин; – время на установку и снятие детали, мин;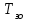 – время на закрепление и открепление детали, мин; – время на закрепление и открепление детали, мин;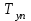 – время на приемы управления, мин; – время на приемы управления, мин;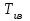 – время на измерение детали, мин. – время на измерение детали, мин.При определении 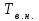 рекомендуется использовать приведенные нижеследующие рекомендации. рекомендуется использовать приведенные нижеследующие рекомендации.Для определения нормы вспомогательного времени используем нормативную информацию для массового производства. Поэтому полученное значение 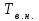 надо будет умножить на коэффициент 1,85. надо будет умножить на коэффициент 1,85.Первоначально определяется масса детали (m), кг (с округлением до десятых): определяем объем цилиндра (заготовки), который умножаем на удельный вес стали (7,8 г/см3) или чугуна (7,0 г/см3). Вспомогательное время на установку и снятие детали вручную при закреплении ее ключом в самоцентрирующем патроне (включает работы: взять деталь, установить и закрепить; открепить деталь, снять и отложить), определяется с использованием данных таблицы 1.2. Таблица 1.2 Вспомогательное время на установку и снятие детали вручную, мин (патроны самоцентрирующие)
Данная установка заготовки выполняется на токарной операции. Для выполнения работы можно воспользоваться следующими данными: - включить или выключить станок: кнопкой – 0,01 мин, рычагом – 0,02 мин; - повернуть резцовую головку на следующую позицию – 0,04 мин; - установить и снять инструмент в быстросменном патроне: при диаметре инструмента до 15 мм – 0,035 мин; до 25 мм – 0,04 мин; до 30 мм – 0,06 мин; свыше 30 мм – 0,08 мин; - поставить кондукторную втулку и снять: при внутреннем диаметре втулки до 20 мм – 0,05 мин; до 40 – 0,06 мин; свыше 40 мм – 0,07 мин; - подвести или отвести инструмент к детали при обработке: резцом – 0,025 мин; сверлом или зенкером – 0,01 мин; фрезой в продольном или поперечном направлении – по 0, 04 мин. Вспомогательное время на приемы управления станком, связанные с перемещением рабочих органов станков, мин, определяется по таблице 1.9. Для выполнения работы можно воспользоваться данными (Туп, мин) таблицы 1.3. Таблица 1.3 Перемещением рабочих органов станков
Вспомогательное время на контрольные промеры (Тиз) универсальным инструментом определяется с использованием следующих данных: - штангенглубиномером при длине паза до 100 мм – 0,18 мин; до 200 мм – 0,2 мин; до 300 мм – 0,22 мин; до 500 – 0,24 мин; - штангенциркулем по таблице 1.4. Таблица 1.4 Вспомогательное время на контрольные промеры штангенциркулем
При этом при точении точность диаметрального размера обеспечивается методом пробных проходов и промеров. Поэтому для вывода режущего инструмента обеспечивается методом пробных проходов и промеров. Поэтому для вывода режущего инструмента на размер потребуется 2-3 раза воспользоваться штангенциркулем. Следовательно, при токарной обработке (двукратной) потребуется для обеспечения заданной точности выполнить в среднем пять измерений штангенциркулем. Кроме того, после выполнения операции потребуется проконтролировать полученные размеры 60 % изготовленных деталей. 1.4. Наименьшая скорость резания, допускаемая кинематикой станка Это техническое ограничение устанавливает взаимосвязь расчетной скорости резания с кинематикой станка (по минимуму). Скорость резания не может быть выбрана меньше, чем возможная при наименьшей частоте вращения шпинделя станка. Это условие записывается в виде следующего неравенства: 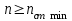 (4) (4)1.5. Наибольшая технологически допустимая скорость резанияЭто техническое ограничение устанавливает взаимосвязь расчетной скорости резания с технологически допустимой наибольшей скоростью резания. Для многих случаев обработки скорость резания не может быть принята больше некоторой величины, которая установлена на основании экспериментальных данных, учитывающих конкретные условия обработки. Это условие записывается в виде следующего неравенства: 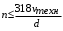 , (5) , (5)где 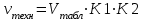 – технологически допустимая скорость резания, определяемая по нормативным картам. – технологически допустимая скорость резания, определяемая по нормативным картам.1.6. Наибольшая скорость резания, допускаемая кинематикой станкаЭто техническое ограничение устанавливает взаимосвязь расчетной скорости резания с кинематикой станка (по максимуму). Скорость резания не может быть выбрана больше, чем возможная, исходя из наибольшей частоты вращения шпинделя станка, т. е. должно иметь место неравенство: 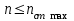 . (6) . (6)1.7. Наименьшая подача, допускаемая кинематикой станка Это техническое ограничение устанавливает взаимосвязь расчетной величины подачи с подачей, допускаемой кинематикой станка (по минимуму): 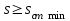 . (7) . (7)1.8. Наибольшая подача, допускаемая кинематикой станка Это техническое ограничение устанавливает взаимосвязь расчетной величины с подачей, допускаемой кинематикой станка (по максимуму): 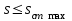 . (8) . (8)1.9 Наибольшая подача, допускаемая требованиями, предъявляемыми к шероховатости обработанной поверхностиЭто техническое ограничение устанавливает взаимосвязь расчетной величины подачи с подачей, допускаемой требованиями, предъявляемыми к шероховатости обработанной поверхности: 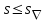 , (9) где , (9) где 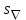 – максимально допустимая подача, обеспечивающая получение данного класса шероховатости обработанной поверхности. – максимально допустимая подача, обеспечивающая получение данного класса шероховатости обработанной поверхности.Для некоторых видов обработки имеются формулы для определения максимальной допустимой подачи 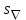 . Например, при продольном наружном точении и подрезке торца . Например, при продольном наружном точении и подрезке торца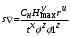 , (10) , (10)где Сн– коэффициент, характеризующий условия обработки; 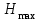 – максимальная высота микронеровностей поверхности в мк; – максимальная высота микронеровностей поверхности в мк;r– радиус закругления при вершине резца в мм; t – глубина резания в мм; – главный угол в плане; 1 – вспомогательный угол в плане. Для упрочняющей обработки 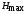 = 5Ra; для точения, строгания и фрезерования = 5Ra; для точения, строгания и фрезерования 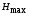 = 6Ra;для остальных методов обработ = 6Ra;для остальных методов обработ 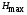 = 7Ra. = 7Ra.При обработке стали и стального литья и стального литья Сн =0,008; y = 1,4; u=0,7; x= 0,3; z= 0,35. При обработке чугуна Сн = 0,045; y= 1,25; u = 0,75; x= 0,25; z= 0,5. Область применения формулы ограничена до 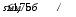 при обработке стали и до при обработке стали и до 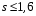 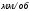 при обработке чугуна. Поэтому на практике для определения максимально допустимой величины при обработке чугуна. Поэтому на практике для определения максимально допустимой величины 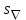 пользуются таблицами, в которых пользуются таблицами, в которых 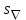 выбирается в зависимости от материала обрабатываемой детали, вспомогательного угла в плане, скорости резания и радиуса при вершине резца. выбирается в зависимости от материала обрабатываемой детали, вспомогательного угла в плане, скорости резания и радиуса при вершине резца.2 Математическая модель процесса резания металловВ общем случае постановка задачи оптимизации режимов обработки включает: выбор искомых параметров; определение множества их возможных значений; выбор анализируемого набора выходных параметров процесса; установление функциональных зависимостей между искомыми и выходными параметрами при фиксированных значениях неуправляемых параметров; выделение целевой функции; назначение диапазонов возможных значений выходных параметров. Анализ рассмотренных видов и критериев оптимальности показывает, что при оптимизации по двум элементам режимов резания n и s без изменения глубины резания, стойкости инструмента и других технических факторов эти оценочные функции при введении ряда упрощений выражаются через n и s достаточно просто. Так, для минимальной себестоимости операции можно записать 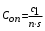 (10) (10)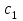 – постоянная величина, не зависящая от режимов резания n и s. – постоянная величина, не зависящая от режимов резания n и s.Для минимального машинного времени можно записать 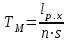 , (11) , (11)где 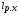 – длина рабочего хода. – длина рабочего хода.Итак, выбранные и описанные выше технические ограничения (1.1.)–(1.9), отражающие с определенной степенью точности физический процесс резания в совокупности с критерием оптимальности (1.10) или (1.11), образуют математическую модель процесса резания. При определении режимов резания широкое применение для двух элементов n и s имеет метод линейного программирования, общая задача которого состоит в определении неотрицательных значений переменных, удовлетворяющих системе ограничений в виде линейных равенств и неравенств и обеспечивающих наибольшее или наименьшее значение некоторой линейной функции – критерия оптимальности. Входящая в уравнения и неравенства величина sв ряде случаев имеет достаточно малые значения, и ей будут соответствовать отрицательные логарифмы. Для того чтобы исключить возможность появления отрицательных логарифмов, умножим во всех уравнениях и неравенствах технических ограничений и критерия оптимальности величину sна 1000и произведем соответствующие преобразования. В результате получим: Для ограничения (1.1): 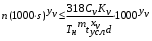 (12) (12)Для ограничения (1.2): 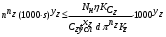 (13) (13)Для ограничения (1.3): 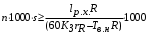 (14) (14)Для ограничения (1. 4): 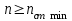 (15) (15)Для ограничения (1.5): 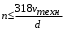 (16) (16)Для ограничения (1.6): 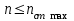 (17) (17)Для ограничения (1.7): 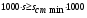 (18) (18) Для ограничения (1.8): 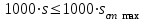 (19) (19)Для ограничения (1.9): 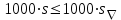 (20) (20)Для уравнения оценочной функции: 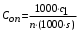 (21) (21)Логарифмируем правые и левые части (12) – (21). В результате получаем: Для ограничения (1.1): 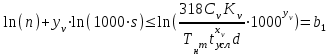 (22) (22)Для ограничения (1.2): 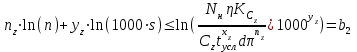 (23) (23)Для ограничения (1.3): 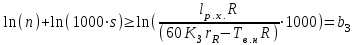 (24) (24)Для ограничения (1.4): 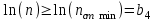 (25) (25)Для ограничения (1.5): 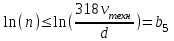 (26) (26)Для ограничения (1.6): 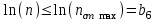 (27) Для ограничения (1.7): (27) Для ограничения (1.7):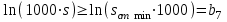 (28) (28)Для ограничения (1.8): 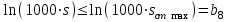 (29) (29)Для ограничения (1.9): 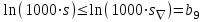 (30) (30)Для уравнения оценочной функции: 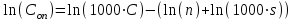 (31) (31)Обозначив через 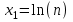 , , 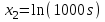 , получим следующую математическую модель оптимального режима резания: , получим следующую математическую модель оптимального режима резания: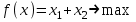 (32) (32)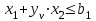 (33) (33)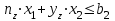 (34) (34)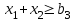 (35) (35)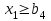 (36) (36)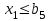 (37) (37)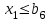 (38) (38)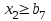 (39) (39)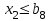 (40) (40)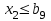 (41) (41)Задача определения оптимального режима резания сводится к отысканию среди всевозможных неотрицательных значений и системы таких значений и, при которых линейная функция принимает максимальное значение. Математическая модель процесса резания может быть изображена в графическом виде. В этом случае каждое техническое ограничение представляется граничной прямой, которая определяет полуплоскость, где возможно существование решений системы неравенств. Граничные прямые, пересекаясь, образуют многоугольник, внутри которого любая точка удовлетворяет всем без исключения неравенствам. Поэтому этот многоугольник принято называть многоугольником решений. Теория линейного программирования показывает, что экстремальное значение оценочной функции (при выпуклом многоугольнике решений) обеспечивается для и, находящихся в точке, лежащей на одной из граничных прямых или их пересечении. Оценочная функция 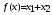 изображается прямой, перпендикулярной к вектору максимизации М(1,1). Так как направление вектора М есть направление возрастания линейной функции f(х), то следует ожидать, что в первой точке касания с многоугольником решения она примет минимальное значение изображается прямой, перпендикулярной к вектору максимизации М(1,1). Так как направление вектора М есть направление возрастания линейной функции f(х), то следует ожидать, что в первой точке касания с многоугольником решения она примет минимальное значение 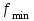 , а в последней точке – максимальное значение , а в последней точке – максимальное значение 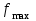 , а координаты этой точки будут являться оптимальным решением системы. , а координаты этой точки будут являться оптимальным решением системы.3 Выполнение расчета в MathCADНа рис. 1.3 показано решение задачи в MathCAD с помощью функции maximize, а на рис. 1.4 – графический способ решения задачи. Рис. 1.3 Решение задачи с помощью функции maximize 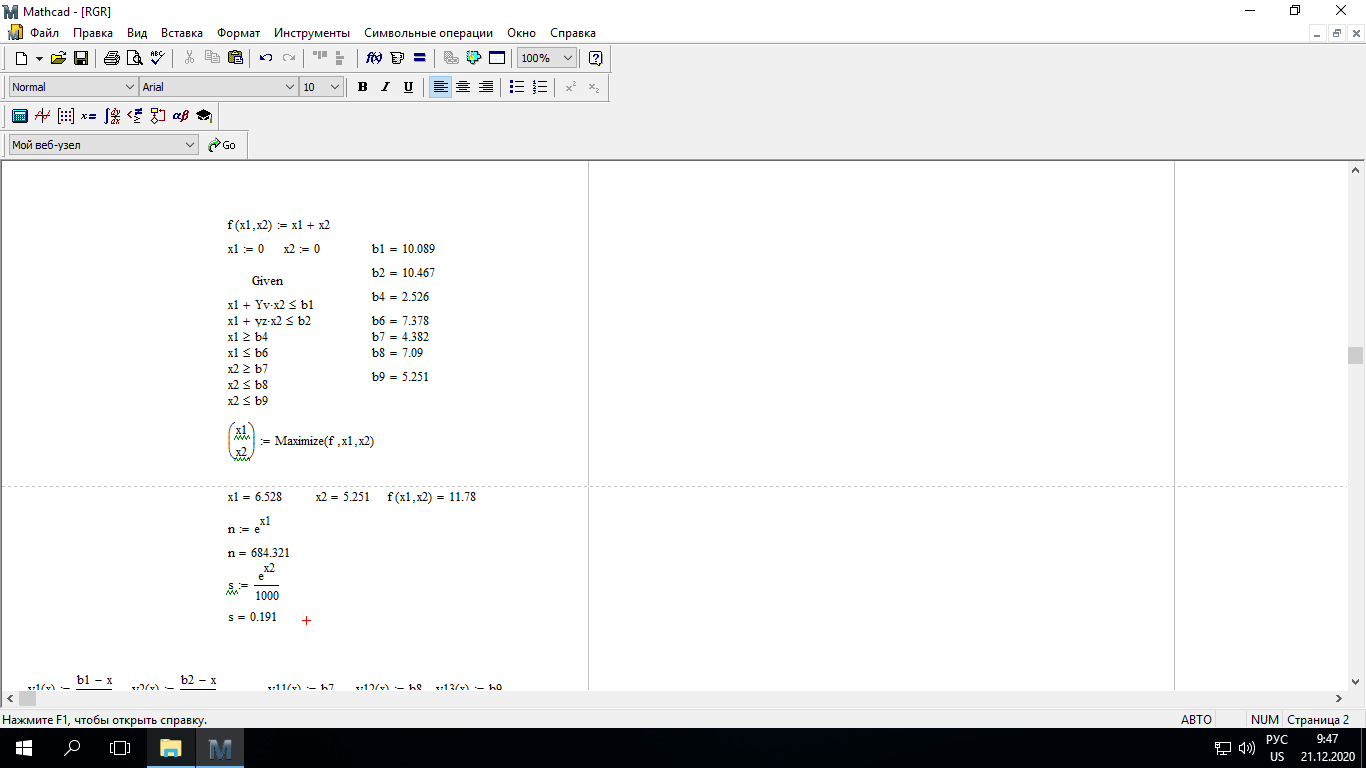 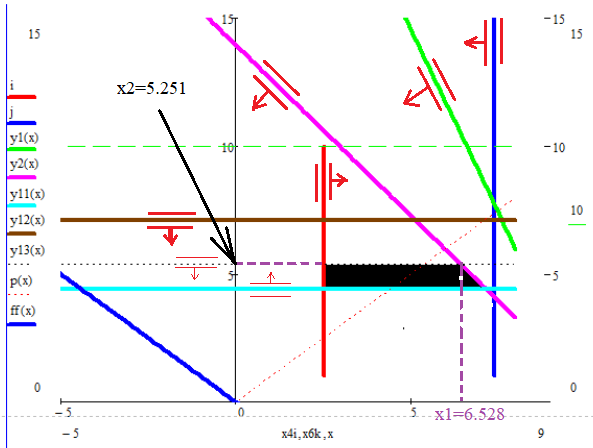 Рис. 1.4 Решение задачи графическим способом в MathCAD ЗаключениеВ ходе выполнения работы я овладела графическим способом решения задач линейного программирования в MathCAD на примере расчета режимов резания для токарной работы. Также при расчете учитывали некоторые ограничения, такие как: мощность электропривода главного движения стана, наибольшая подача, допускаемая кинематикой станка, заданная производительность станка на проектируемой операции, режущие возможности инструмента, и другие ограничения. Список используемых источниковСправочник технолога-машиностроителя. В 2-х т. Т.2 /Под ред. А.Н.Малова – М.: Машиностроение, 1972. - 568с. Общемашиностроительные нормативы режимов резания для технического нормирования работ на металлорежущих станках. Ч.1 /Изд.2 – М.: Машиностроение, 1974. - 416с. Инструментальные материалы /В.Ф.Моисеев, С.Н.Григорьев – М.: ИЦ МГТУ «Станкин», Янус-К. – 2005, 248 с. Резание металлов: Учебное пособие /Е.Н.Трембач и др. – Йошкар-Ола: МарГТУ, 2005. – 396 с. Приложение А – Листинг программы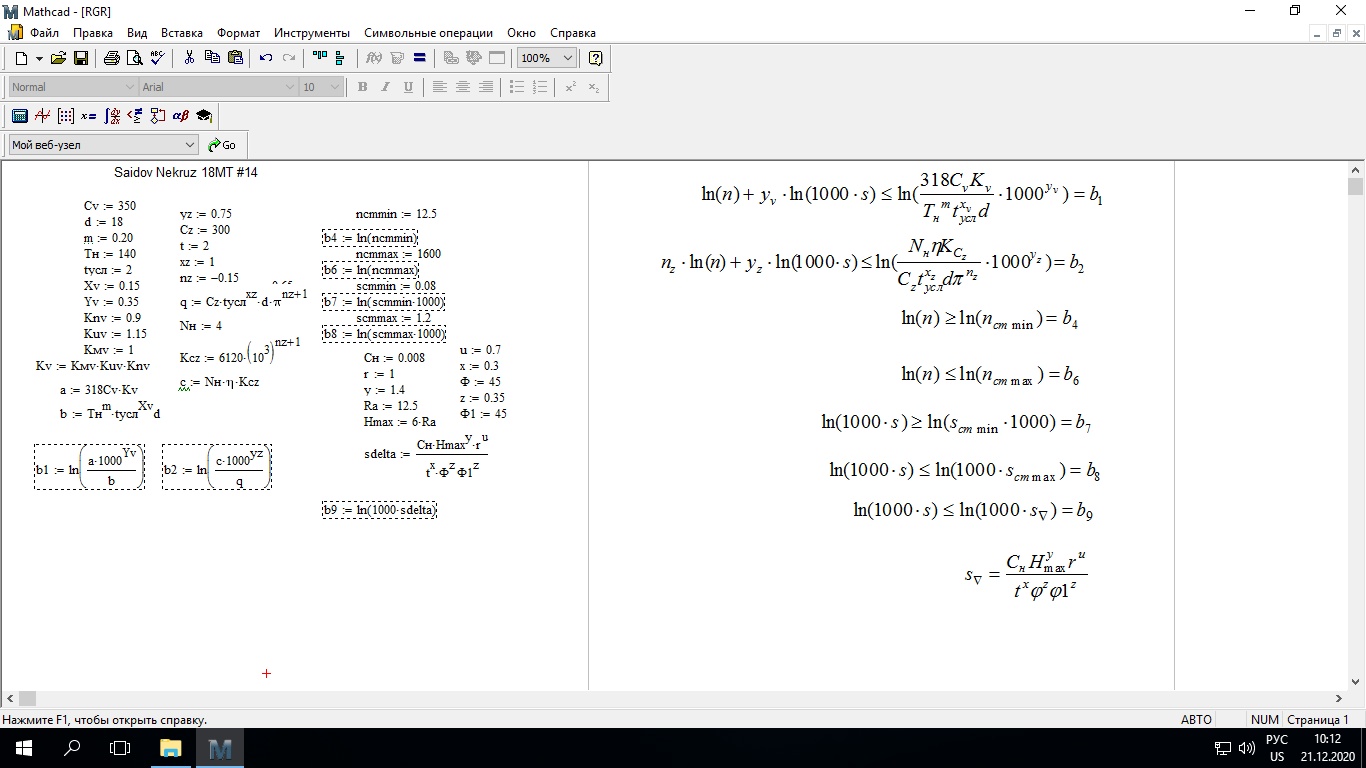 Продолжение приложения А– Листинг программы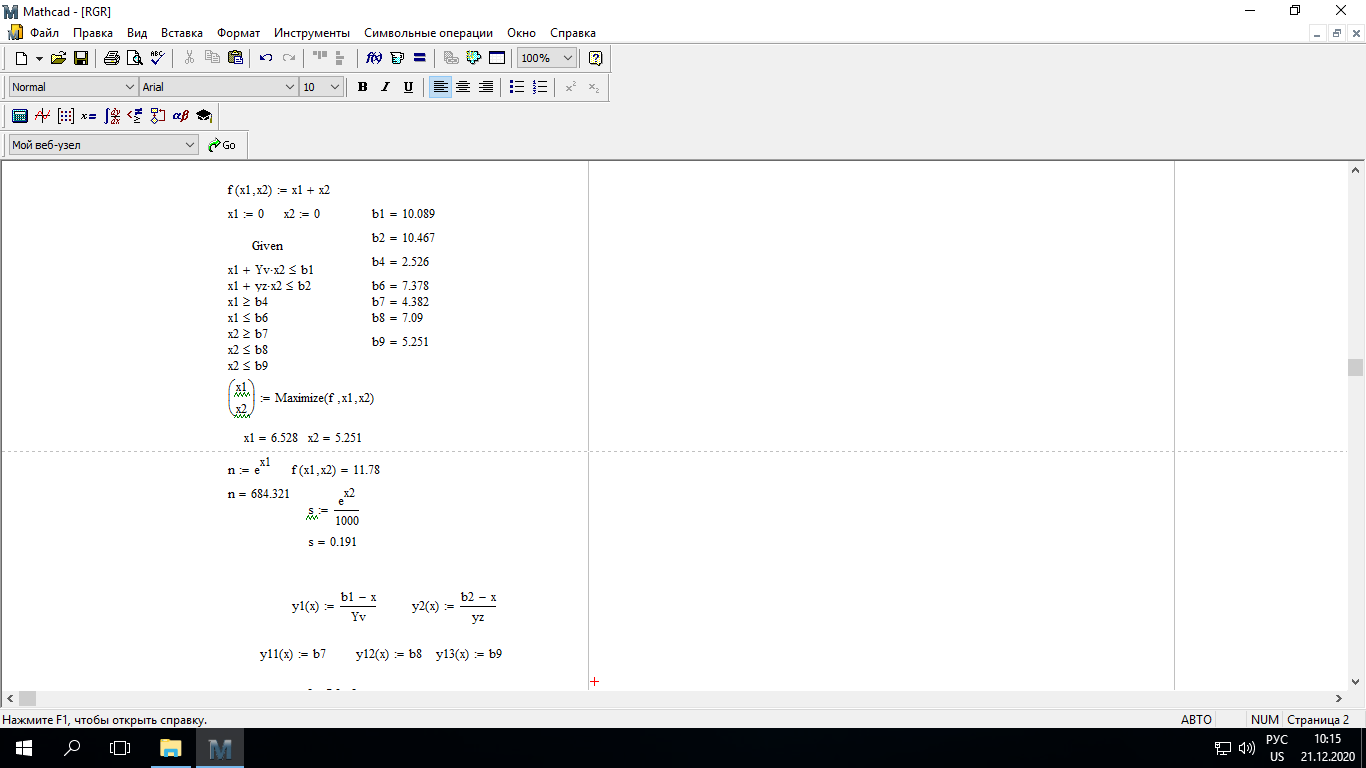 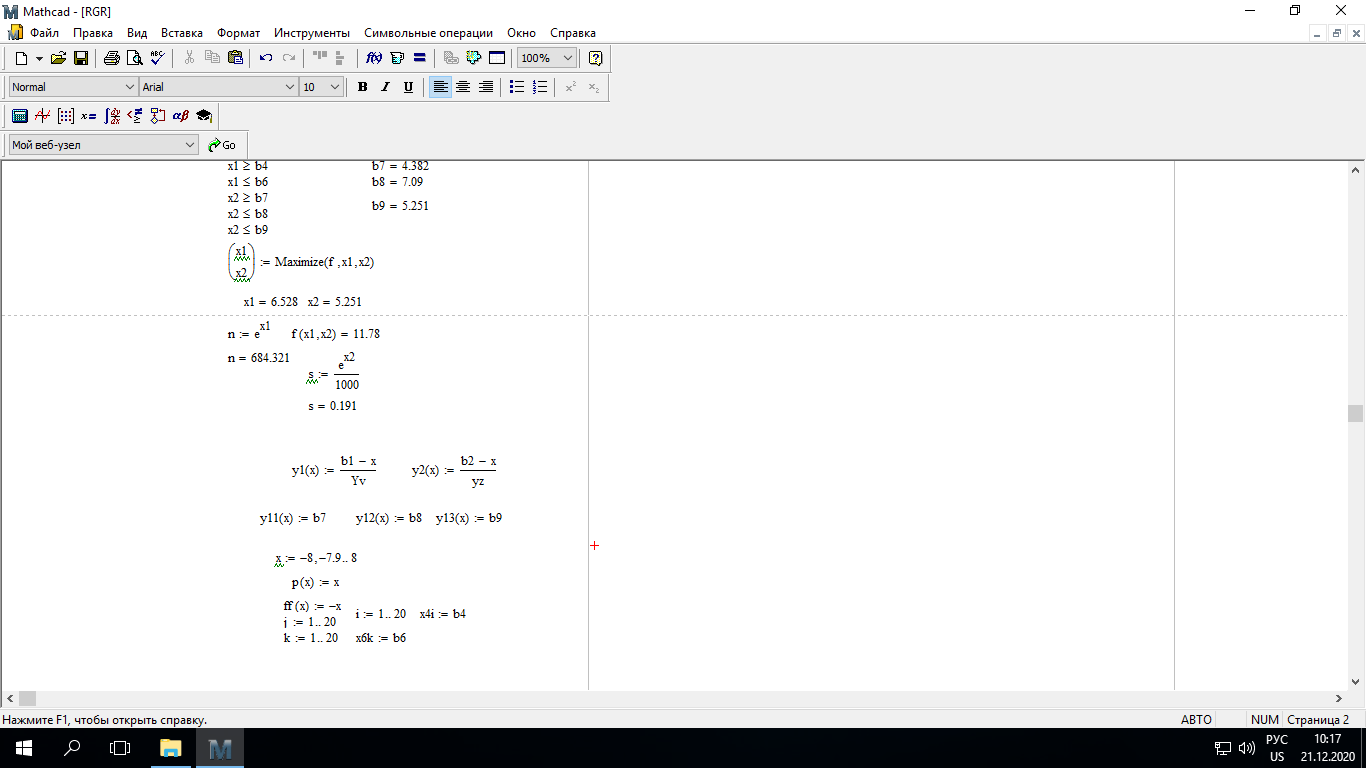 Окончание приложения А– Листинг программы Окончание приложения А– Листинг программы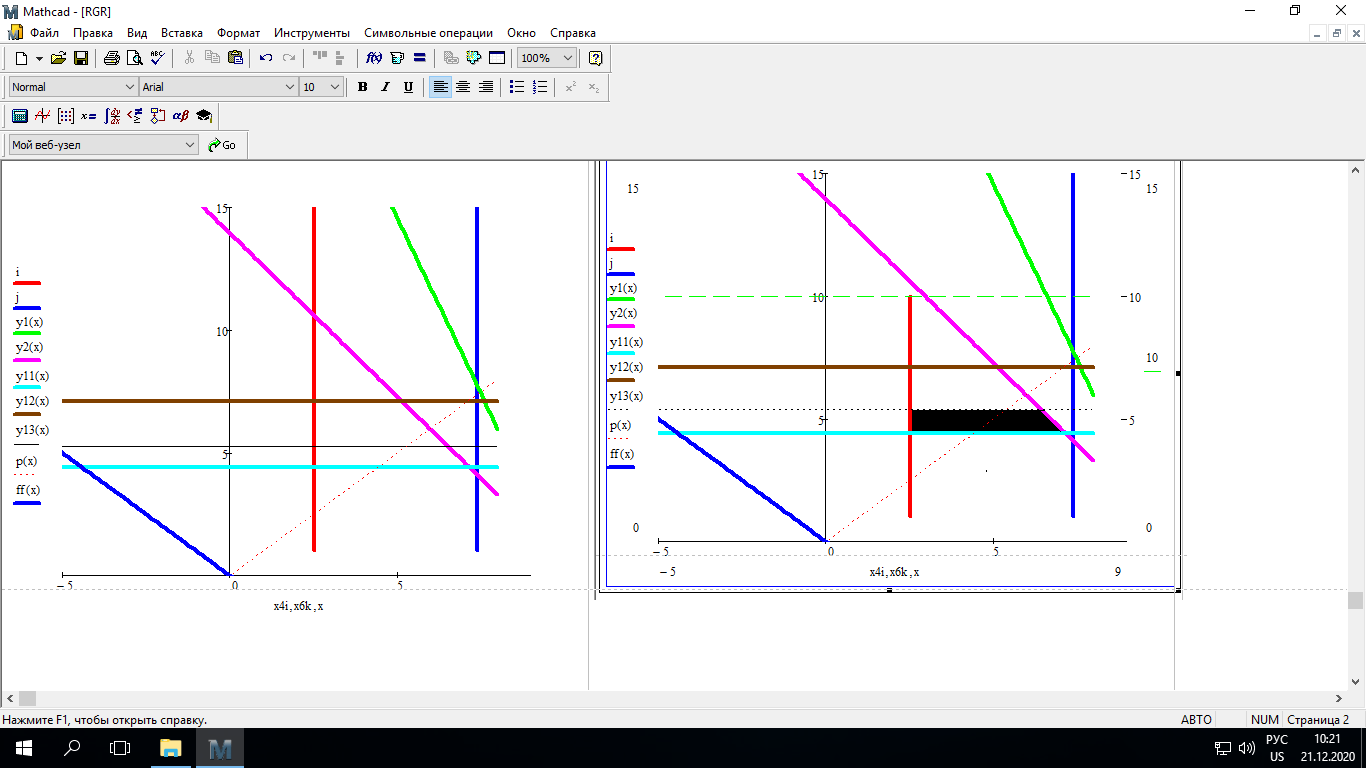 Разраб. Изм. Лист № докум. Ахатов Б.Д. Подпись Дата ПензГТУ 2.15.03.05.014 ПЗ Листов Лист Лит. 3 нято называть коэффициентом серийности. ве или аналогично технологического процесса. П К Кафедра ТМС Группа 19МТ1бпв Провер. Колодяжный Н. контр. Утв. Проектирование электромеханического привода | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
