ДифГеометрия. ДифГеом 13заданий. Практическая часть 13 заданий
 Скачать 51.88 Kb. Скачать 51.88 Kb.
|
|
Практическая часть 13 заданий Вычислите кривизну линии 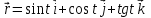 в точке в точке 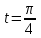 . .Для вычисления кривизны данной линии воспользуемся формулой 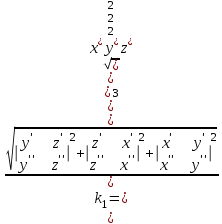 так как линия задана векторным уравнением. так как линия задана векторным уравнением.Координаты векторов: 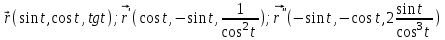 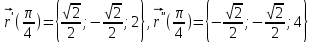 Найдем корень квадратный от суммы квадратов матриц: 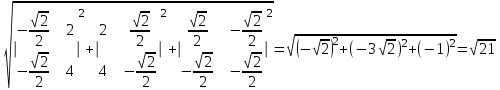 По формуле найдем знаменатель: 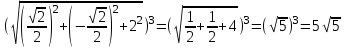 Таким образом, кривизна линии в точке пи/4 равна 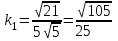 Составьте уравнение касательной прямой и нормальной плоскости винтовой линии 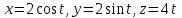 в точке в точке 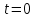 . .Точка М имеет координаты 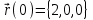 Найдем производную и его значение в этой точке 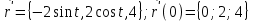 Уравнение касательной 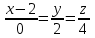 Уравнение нормальной плоскости 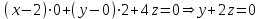 Вычислите кручение линии 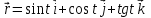 в точке в точке 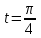 . .Вычислите кручение линии 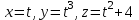 в точке в точке 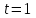 . .Найдите первую квадратичную форму геликоида, заданного уравнениями 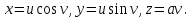 Найдите первую квадратичную форму тора 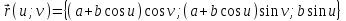 Дана поверхность 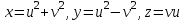 , где , где 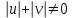 найдите первую квадратичную форму поверхности. найдите первую квадратичную форму поверхности.Найдите площадь четырёхугольника на геликоиде 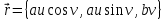 , ограниченного линиями , ограниченного линиями 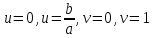 . .Найдите площадь четырехугольника на прямом геликоиде, ограниченного линиями 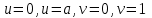 с первой квадратичной формой с первой квадратичной формой 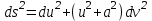 . .Найдите вторую квадратичную форму поверхности 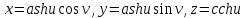 Найдите полную и среднюю кривизну прямого геликоида 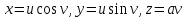 . .Определите асимптотические линии катеноида 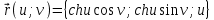 . .Найдите вторую квадратичную форму поверхности 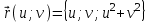 . . |
