Математика. математека. Практическая Работа 1. Множества и операции над ними. Объединение, пересечние, разность, дополнение. Разбиение, булеан. Цель работы
 Скачать 16.33 Kb. Скачать 16.33 Kb.
|
|
Практическая Работа №1. Множества и операции над ними. Объединение, пересечние, разность, дополнение. Разбиение, булеан. Цель работы Повторение основных понятий теории множеств, изучение операций над ними приобретение навыков решения задач. Задачи Дано: а) A, B ⊆ Z, A = {-1;0;9;17}, B = {-1;1;9;10;25}. б) A,B ⊆ R, A = [-4;9), B = (-5;7]. Найти: A ∩ B, A ∪ B, A \ B, B \ A, ¬ B Решение А) A ∩ B включает в себя все элементы, принадлежащие одновременно каждому из множеств A и B. Таким образом: A ∩ B={-1,9} A ∪ B включает в себя все элементы, принадлежащие хотя бы одному из множеств A или B. Таким образом: A ∪ B={-1,0,1,9,10,17,25} A \ B состоит из всех элементов А, которые не принадлежат В, поэтому: A \ B={0,17} B \ A состоит из всех элементов B, которые не принадлежат A, поэтому: B \ A={1,10,25} ¬ B={0,17} Б) А={-4,-3,-2,-1,0,1,2,3,4,5,6,7,8} B={-4,-3,-2,-1,0,1,2,3,4,5,6,7} A ∩ B={-4,-3,-2,-1,0,1,2,3,4,5,6,7} A ∪ B={-4,-3,-2,-1,0,1,2,3,4,5,6,7,8} A \ B={8} B \ A={ 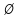 } }Практическая Работа №2. Решение комбинаторных задач. Подстановки, алгебра подстановок. Решение комбинаторных задач с использованием метода включения и исключения. Задача о встречах Цель работы Приобретение навыков работы с комбинаторными конфигурациями, использования разработанных методов решения задач. Задачи Сколько разных слов можно получить из слова «абракадабра»? Сколько разных слов можно получить из слова «абракадабра», если необходимо, чтобы слова начинались с буквы «к»? Сколько разных слов можно получить из слова «абракадабра», если необходимо, чтобы в них обе буквы «б» стояли рядом? Решение Если есть n1 элемент 1-го вида, n2 элементов 2-го вида, ..., nk элементов k-го вида, и n1+n2+...+nk=n , то количество перестановок этих n элементов равно 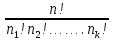 Имеем такой инвентарь: ААААА ББ РР К Д 1) разных слов будет 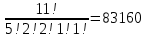 2) если слово начинается на К, поставим К сразу на первое место и будем рассматривать различные перестановки уже 10-и букв, а их будет 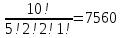 3) комбинацию ББ примем за одну букву, тогда букв опять 10 и убирается повторение буквы Б, и перестановок будет 3) комбинацию ББ примем за одну букву, тогда букв опять 10 и убирается повторение буквы Б, и перестановок будет 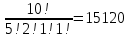 |
