Пр занятие 1.ИмитМод. Практическая работа 1 Теоретические сведения Поток событий

Название	Практическая работа 1 Теоретические сведения Поток событий
Дата	03.10.2018
Размер	207.93 Kb.
Формат файла
Имя файла	Пр занятие 1.ИмитМод.docx
Тип	Практическая работа #52300

Практическая работа №1

Теоретические сведения

Поток событий – последовательность однотипных ситуаций, наступающих одна за другой в случайные моменты времени (пример, поток отказов и поток восстановлений, поток вызовов на телефонной станции, поток покупателей в магазине).

Поток событий можно наглядно изобразить рядом точек на оси времени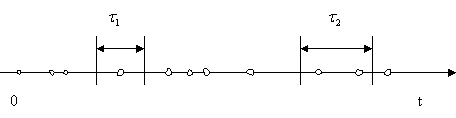

Рисунок - Изображение потока событий на оси времени

Характеристики потоков событий:

Интенсивность потока событий () – это среднее число событий, приходящееся на единицу времени.
Регулярность, поток называют регулярным если события следуют одно за другим через равные промежутки времени
стационарность, поток называется стационарным, если его вероятностные характеристики не зависят от времени.
Отсутствие последствия, поток называется потоком без последствия, если для любых двух непересекающихся отрезков и число событий, попадающих на один из отрезков, не зависит от числа событий, попадающих на др.
Ординарность, поток событий называется ординарным, если события в нем появляются поодиночке, а не группами по нескольку сразу.

Поток событий называется простейшим (или стационарным пуассоновским), если он обладает сразу тремя свойствами: 1) стационарен, 2) ординарен, 3) отсут-ие последействия. Простейший поток обязательное понятие для аналит-го моделирования.

Для простейшего потока с интенсивностью

интервал t между соседними событиями имеет так называемое показательное (экспоненциальное) распределение с плотностью

где - параметр показательного закона, t>0.

Примерами могут быть:

- поток вызовов на телефонной станции;

- поток включений приборов в бытовой электросети;

- поток грузовых составов, поступающих на железнодорожную станцию;

- поток неисправностей (сбоев) вычислительной машины;

- поток выстрелов, направляемых на цель, и т. д.

Простейшим потоком вызовов называется стационарный ординарный поток без последействия. Основные характерные свойства простейшего потока выражают следующие определения этого потока:

1.) ординарный поток без последействия с постоянным параметром λ (0<λ<∞);

2.) интенсивность простейшего потока равна его параметру μ=λ;

3.) поток без последействия, для которого вероятность P_i(t) поступления i вызовов на промежутке длиной t определяется формулой (распределением) Пуассона:

,

Вероятность не поступления ни одного соб (i=0):

Противоположное событие: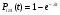

4.) поток с независимыми промежутками z_k (k=1,2,…) между вызовами, распределенными по одинаковому экспоненциальному закону:

,

5а.) плотность распределения вероятностей промежутков времени между вызовами: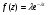

,

5б.) распределения промежутка времени между вызовами подчинено показательному закону и является достаточным условием существования простейшего потока;

6.) если известно, что случайный промежуток времени z, распределенный по показательному закону длится уже некоторое время τ, то закон распределения оставшейся части промежутка будет также показательным и с тем же параметром μ не будет зависеть от τ;

7.) объединение независимых простейших потоков с параметрами λ₁, λ₂, λ₃ очевидно, тоже будет простейшим потоком с параметром (λ₁+ λ₂+ λ₃);

Рис 1.4. Разъединение и объединение Пуассоновского потока.

8.) сумма большого числа малых станционных потоков близка к простейшему;

9.) математическое ожидание промежутка z между вызовами:

,

10.) дисперсия промежутка z между вызовами:

,

11.) среднеквадратическое отклонение промежутка t:

,

12.) математическое ожидание числа вызовов за промежуток t: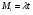

,

13.) дисперсия числа вызовов за промежуток t:

,

14.) совпадение за промежуток для простейшего потока на практике удобно использовать при проверке соответствия реального потока модели простейшего потока времени между вызовами подчинено показательному закону и является достаточным условием существования простейшего потока.

Задания к практической работе

Задание.

Из таблиц Приложения согласно варианту, заданному преподавателем, выписать задачу.
С помощью программы MS Excel рассчитать теоретические значения частоты требований, соответствующие пуассоновскому потоку.
Сравнить теоретические значения частоты требований и практические, заданные по варианту.
Сделать вывод, является ли заданный по варианту поток простейшим Пуассоновским.

Вариант 1