Практическая работа 10. Создаем диаграммы, графики, схемы, графы, деревья. Записываем число, тему урока Посмотреть видео
 Скачать 1 Mb. Скачать 1 Mb.
|
|
23 марта Классная работа Многообразие схем. Информационные модели на графах. Деревья. Использование графов при решении задач. Практическая работа №10. Создаем диаграммы, графики, схемы, графы, деревья. Записываем число, тему урока Посмотреть видео https://www.youtube.com/watch?v=PurV65nwfaQ Сегодня мы узнаем: Какие информационные модели называются графами, для чего применяются графы, и как с помощью графов решать задачи. Граф — это группа объектов со связями между ними. Объекты представляются как вершины графа, а связи — это линии соединяющие вершины. Например, все шестиклассники пользуются мобильными телефонами и многие общаются друг с другом через SMS. В данном примере вершины графа – это отдельные ребята, а связи – это процесс «пишут друг другу SMS».  Вершины графа можно изображать по-разному. Это может быть овал либо круг, точка или прямоугольник. 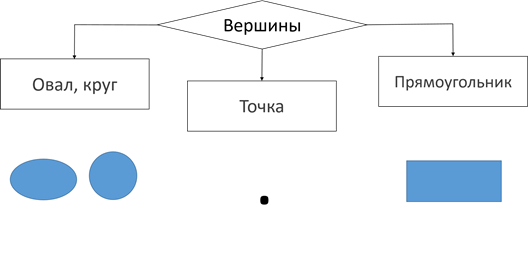 Разберёмся более подробно со связями, то есть с линиями, соединяющими вершины графа. Дуга Если линия, соединяющая вершины графа направленная, то есть со стрелкой, то она называется дугой. 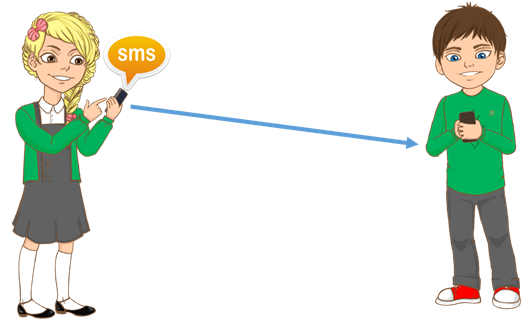 То есть дугой называется направленная линия, соединяющая вершины графа. Ребро Если линия ненаправленная, то есть, нет стрелки, то эта линия называется ребром.  Ребро – это ненаправленная линия, которая соединяет вершины графа. Петля Если линия выходит из некоторой вершины и входит в неё же, то эта линия называется петлёй. 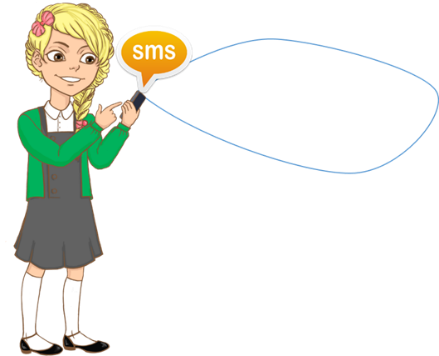 Петля – это линия, которая выходит из некоторой вершины и входит в нее же Вернёмся к примеру, с шестиклассниками. Здесь система – это ученики шестого класса в какой-то школе. Мы, объекты этой системы (т.е. отдельных ребят) изобразили вершинами, и соединили вершины ненаправленными линиями (рёбрами). Ребра в данном случае являются двухсторонними отношениями, потому что ребята пишут SMS-ки друг другу. Мы получили информационную модель рассматриваемой системы в форме графа. 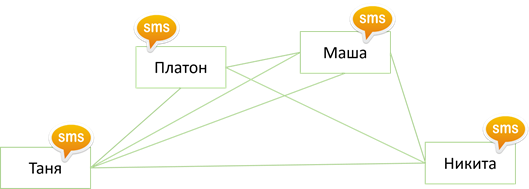 Рассмотрим виды графов. Если вершины графа соединены рёбрами, то такой граф называется неориентированным. Рассмотрим пример: Таня написала SMS Никите, Никита ответил Тане, Таня написала Маше, Маша ответила Тане, Никита написал Маше. Здесь ребята отвечали друг другу на смски. 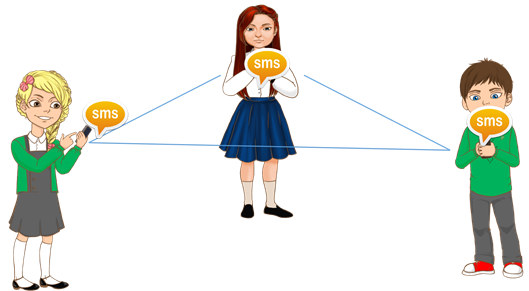 Данное отношение называется цепью графа. Цепь графа – это путь по вершинам и рёбрам графа, который включает любое ребро не меньше одного раза. Если в цепи начальная и конечная вершины совпадают, то такая цепь называется циклом. Например, Таня написала SMS Никите, Никита – Маше, Маша – Платону, а Платон написал Тане. Здесь цикл – это цепь Таня – Никита – Маша – Платон – Таня. 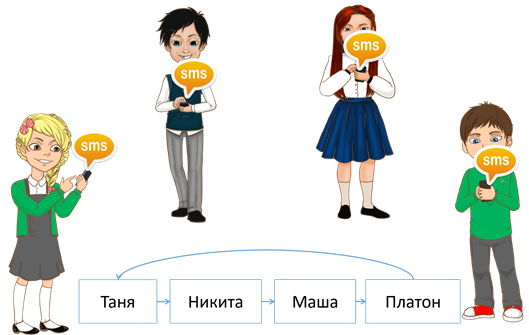 Далее, рассмотрим следующий вид графа. Если вершины графа соединены дугами (стрелками), то такой граф называется ориентированным. В нашем примере цепь будет выглядеть следующим образом: Таня написала SMS Никите, Никита – Маше, Маша – Платону. То есть СМС-ки были без ответа.  Рассмотрим следующий пример: Город Москва основан в 1147 году, город Санкт-Петербург основан в1703 году. Расстояние от Москвы до Санкт-Петербурга 713 км. Год основания города Тверь 1135 год, расстояние от Москвы до Твери 175 км. Ярославль основан в 1010 год, расстояние от Москвы до Ярославля 272 км. Город Смоленск основан в 863 году, а расстояние от Москвы до Смоленска 400 км. 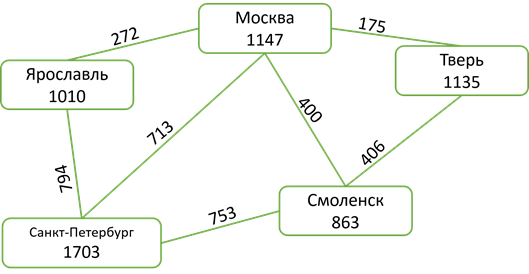 Мы получили взвешенный граф. Взвешенным называется граф, который характеризуется дополнительной информацией – весом вершины или весом ребра (дуги). Рассмотрим следующий вид графа с циклами, то есть граф, в цепи которого начальная и конечная вершины совпадают. Помните сказку о царе Салтане? Давайте построим граф по отрывкам из сказки. К морю лишь подходит он, Вот и слышит будто стон... Бьётся лебедь средь зыбей, Коршун носится над ней; Но как раз стрела запела, В шею коршуна задела — Коршун в море кровь пролил, Лук царевич опустил; Смотрит: коршун в море тонет И не птичьим криком стонет, Лебедь около плывёт, Злого коршуна клюёт, И царевичу потом Молвит русским языком… Вот открыл царевич очи; Отрясая грёзы ночи И дивясь, перед собой Видит город он большой, Мать и сын идут ко граду. Лишь ступили за ограду, Пышный двор встречает их; Все их громко величают И царевича венчают Княжий шапкой, и главой Возглашают над собой… И так далее. Мы получили граф с циклами, который называется сетью. Если раньше мы рассматривали примеры, в которых связи были одинаковые (ребята писали смски), то в данном примере связи различны. Поэтому мы их подписывали. 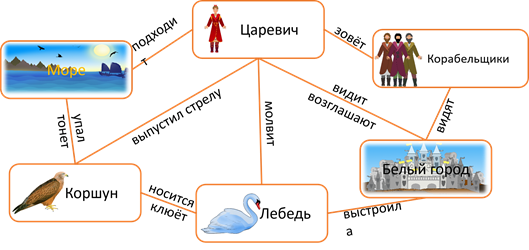 Следующий вид графа, называется дерево. Дерево – это граф с иерархической системой, где Иерархия – это структура распределения частей целого от высшего к низшему. А Иерархическая система – это система, части которой находятся в определённых отношениях. К отношениям иерархической системы относятся «является разновидностью», «входит в состав» и другие «отношения подчинённости».  Рассмотрим иерархическую систему фирмы, которая, например, занимается реализацией техники. Здесь будет такая система подчинённости: генеральный директор - самый главный человек и владелец фирмы, ему подчиняются директора магазинов, которые руководят работой администраторов, ну а тем, в свою очередь, подчиняются продавцы.  Рассмотрим систему, связанную системой подчинённости «входят в состав». Она имеет иерархическую структуру. Например, изобразим следующий граф иерархической системы: Периодическая система элементов в неё состав входят металлы и неметаллы. В свою очередь металлы делятся на 2 группы – группа 1 и группа 2, неметаллы делятся также на 2 группы – группа 5 и группа 6 и так далее. В отличие от остальных графов дерево не содержит циклов и петель, так как между любыми двумя его вершинами существует только один путь. Так же у графа «Дерево» выделяется главная вершина, которая называется корень дерева. У любой вершины дерева могут быть потомки. А вершины, у которых нет потомков, называются листьями. 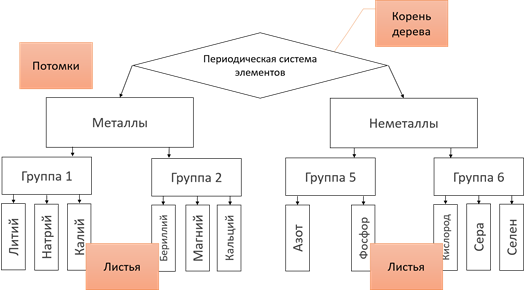 Некоторые виды задач удобно решать с помощью графов. Давайте решим одну из задач. Выполняем в тетради. В коробке три шарика: жёлтый, зелёный и красный. Шестиклассница Таня со своими двумя друзьями Машей и Никитой вынимают их из коробки по одному. Сколько комбинаций выбора при этом возможно? Нужно выписать все варианты выбора. Решение данной задачи удобно представить в виде дерева. Возьмём за корневую вершину произвольную току О., Таня может взять из коробки один из трёх шариков. Обозначим их буквами Ж, З и К. На схеме это соответствует трём ветвям, исходящим из точки О. Первый уровень в нашей задаче – это выбор Тани. Теперь мы будем строить второй уровень графа. Второй уровень – это выбор Никиты. Если Таня взяла жёлтый шарик, то Никита может взять зелёный или красный. Если же Таня взяла зелёный шарик, то Никита может взять жёлтый или красный. Аналогично, если Таня взяла красный шарик, то Никита может взять жёлтый или зелёный. Осталось построить третий уровень, который отображает выбор Маши. Маша в каждом случае может взять оставшийся шарик. То есть если Таня взяла жёлтый шарик, а Никита зелёный, то Таня возьмёт красный шарик. Следующий вариант: если Таня взяла жёлтый шарик, а Никита Красный, Маша возьмёт зелёный шарик. И так далее мы достраиваем оставшиеся ветви. Выпишем все пути от вершин первого уровня к вершине третьего. Каждый из выписанных путей определяет один из вариантов вытягивания шестиклассниками шариков из коробки. Так как других путей нет, то искомое число вариантов – 6. 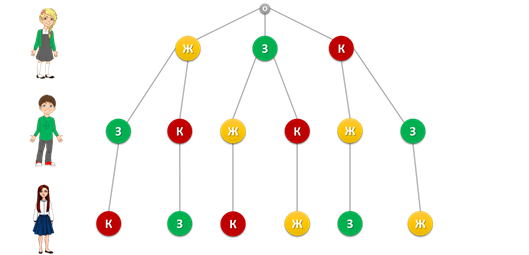 Если при решении задачи не нужно указывать все возможные варианты, а нужно просто указать их число, то дерево можно и не строить. Тогда рассуждаем так: Таня может взять один из трёх шариков, Никита может взять один из двух оставшихся шариков, а Маша – один оставшийся. Получаем: 3, умножить на 2, умножить на 1 получаем ответ – 6 вариантов. Итак, сегодня на уроке мы узнали: Граф является наглядным средством представления информации состава и структуры системы. Дерево – это граф с иерархической системой. Отличительная особенность дерева – это то, что между любыми двумя вершинами существует единственный путь. Иерархия – это структура распределения частей целого от высшего к низшему. Иерархическая система – это система, части которой находятся в отношениях подчинённости «является разновидностью», «входит в состав» и других. Практическая работа. Выполнить задание №4 стр. 191 (файл Погода.doc прилагается), задание №4 стр. 194 Все задания выполнять в одном документе с расширением *.doc. Имя файла фамилия класс, например Иванова6А.doc На проверку присылают работы все ученики. Если нет возможности выполнить в электронном варианте, то выполняете работу в тетради и присылаете фото. Домашние задание (присылают все девочки): 1.Уч.§13 стр. 96-99. Письменно выполнить задание стр. 99 задание № 6. 2. В школьной столовой на обед приготовили в качестве вторых блюд мясо, котлеты и рыбу. На сладкое-мороженое, фрукты и пирог. Каждый может выбрать одно второе блюдо и одно блюдо на десерт. Сколько существует различных вариантов для одного обеда? Изобразите их с помощью графа. |
