Практическая работа №2. Арифметические операции в Python.
Язык Python, благодаря наличию огромного количества библиотек для решения разного рода вычислительных задач, сегодня является конкурентом таким пакетам как Matlab и Octave. Запущенный в интерактивном режиме, он, фактически, превращается в мощный калькулятор.
Что изучим?
Арифметические операции над числами, работу с комплексными числами , битовые операция,
Представление чисел в разных системах исчисления
Библиотеки math.
Что мы знаем?
типы и модели данных Python
1.1 в языке Python существует три встроенных числовых типа данных:
целые числа (int);
вещественные числа (float);
комплексные числа (complex).
Если в качестве операндов некоторого арифметического выражения используются только целые числа, то результат тоже будет целое число.* Исключением является операция деления, результатом которой является вещественное число.
При совместном использовании целочисленных и вещественных переменных, результат будет вещественным.
Арифметические операции с целыми и вещественными числами
Все эксперименты будем производить в Python, запущенном в интерактивном режиме.
Сложение.
Складывать можно непосредственно сами числа…
>>> 3+2
5
либо переменные, но они должны предварительно быть проинициализированы.
>>> a = 3
>>> b = 2
>>> a + b
5
Результат операции сложения можно присвоить другой переменной…
>>> a = 3
>>> b = 2
>>> c = a + b
>>> print(c)
5
либо ей же самой, в таком случае можно использовать полную или сокращенную запись, полная выглядит так
>>> a = 3
>>> b = 2
>>> a = a + b
>>> print(a)
сокращенная так
>>> a = 3
>>> b = 2
>>> a += b
>>> print(a)
5
Все перечисленные выше варианты использования операции сложения могут быть применены для всех нижеследующих операций.
Вычитание.
>>> 4-2
2
>>> a = 5
>>> b = 7
>>> a - b
-2
Умножение.
>>> 5 * 8
40
>>> a = 4
>>> a *= 10
>>> print(a)
40
Деление.
>>> 9 / 3
3.0
>>> a = 7
>>> b = 4
>>> a / b
1.75
Получение целой части от деления.
>>> 9 // 3
3
>>> a = 7
>>> b = 4
>>> a // b
1
Получение остатка от деления.
>>> 9 % 5
4
>>> a = 7
>>> b = 4
>>> a % b
3
Возведение в степень.
>>> 5 ** 4
625
>>> a = 4
>>> b = 3
>>> a ** b
64
Работа с комплексными числами
Для создания комплексного числа можно использовать функцию complex(a, b), в которую, в качестве первого аргумента, передается действительная часть, в качестве второго – мнимая. Либо записать число в виде a + bj.
Рассмотрим несколько примеров.
Создание комплексного числа.
>>> z = 1 + 2j
>>> print(z)
(1+2j)
>>> x = complex(3, 2)
>>> print(x)
(3+2j)
Комплексные числа можно складывать, вычитать, умножать, делить и возводить в степень.
>>> x + z
(4+4j)
>>> x - z
(2+0j)
>>> x * z
(-1+8j)
>>> x / z
(1.4-0.8j)
>>> x ** z
(-1.1122722036363393-0.012635185355335208j)
>>> x ** 3
(-9+46j)
У комплексного числа можно извлечь действительную и мнимую части.
>>> x = 3 + 2j
>>> x.real
3.0
>>> x.imag
2.0
Для получения комплексно сопряженного числа необходимо использовать метод conjugate().
>>> x.conjugate()
(3-2j)
Битовые операции
В Python доступны битовые операции, их можно производить над целыми числами.
Побитовое И (AND).
>>> p = 9
>>> q = 3
>>> p & q
1
Побитовое ИЛИ (OR).
>>> p | q
11
Побитовое Исключающее ИЛИ (XOR).
>>> p ^ q
10
Инверсия.
>>> p
-10
Сдвиг вправо и влево.
>>> p << 1
18
>>> p >> 1
4
Повторение*: Набрать задание и проверить
>>> a
2
>>> b
3
>>> c=a*b
>>> print (c)
6
>>> d=a**b
>>> print(d)
8
>>> d==c
False
>>> d>c
True
>>> z=1+2j
>>> print(z)
(1+2j)
>>> y=complex(10.6)
>>> print(y)
(10.6+0j)
>>> v=complex(10.5,8)
>>> print(v)
(10.5+8j)
>>> k=z+v-y
>>> print(k)
(0.9000000000000004+10j)
Представление чисел в других системах счисления
В своей повседневной жизни мы используем десятичную систему исчисления, но при программирования, очень часто, приходится работать с шестнадцатеричной, двоичной и восьмеричной.
Представление числа в шестнадцатеричной системе
>>> m = 124504
>>> hex(m)
'0x1e658'
Представление числа в восьмеричной системе
>>> oct(m)
'0o363130'
Представление числа в двоичной системе
>>> bin(m)
'0b11110011001011000'
Библиотека (модуль) math
В стандартную поставку Python входит библиотека math, в которой содержится большое количество часто используемых математических функций.
Для работы с данным модулем его предварительно нужно импортировать.
>>> import math
Рассмотрим наиболее часто используемые функции.
math.ceil(x)
Возвращает ближайшее целое число большее, чем x.
>>> math.ceil(3.2)
4
math.fabs(x)
Возвращает абсолютное значение числа.
>>> math.fabs(-7)
7.0
math.factorial(x)
Вычисляет факториал x.
>>> math.factorial(5)
120
math.floor(x)
Возвращает ближайшее целое число меньшее, чем x.
>>> math.floor(3.2)
3
math.exp(x)
Вычисляет e**x.
>>> math.exp(3)
20.085536923187668
math.log2(x)
Логарифм по основанию 2.
math.log10(x)
Логарифм по основанию 10.
math.log(x[, base])
По умолчанию вычисляет логарифм по основанию e, дополнительно можно указать основание логарифма.
>>> math.log2(8)
3.0
>>> math.log10(1000)
3.0
>>> math.log(5)
1.6094379124341003
>>> math.log(4, 8)
0.6666666666666667
math.pow(x, y)
Вычисляет значение x в степени y.
>>> math.pow(3, 4)
81.0
math.sqrt(x)
Корень квадратный от x.
>>> math.sqrt(25)
5.0
Тригонометрические функции.
math.cos(x)
math.sin(x)
math.tan(x)
math.acos(x)
math.asin(x)
math.atan(x)
Число пи.
math.pi
Число е.
math.e
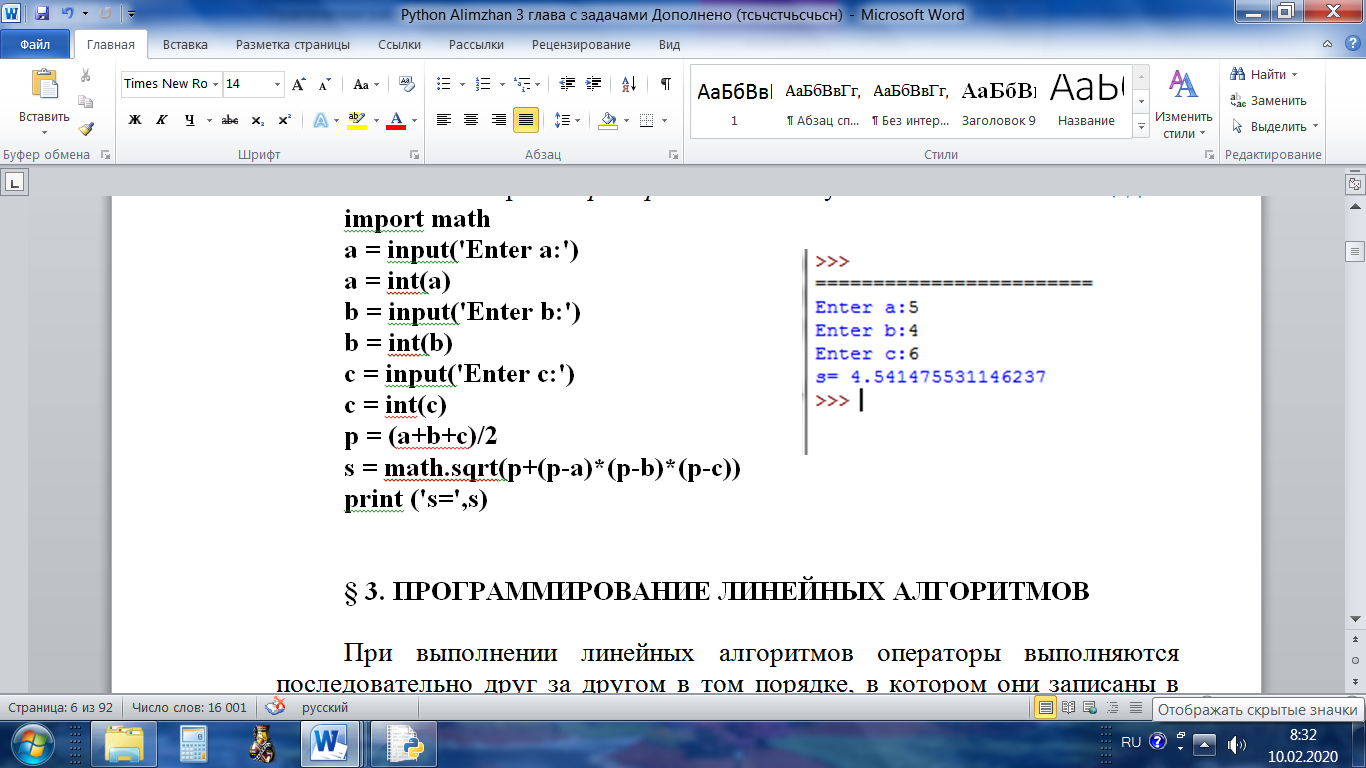
Составьте алгоритм Примера 1 Вычисление площади
на языке Python:
Пример 2. Запишите с использованием промежуточных величин алгоритм вычисления выражения:
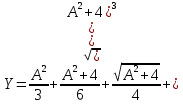
В качестве промежуточных величин используем переменные В, Z, значения которых заменяют многократно повторяющиеся действия, что позволяет сделать алгоритм более эффективным. Как сделать программу еще компактнее ?
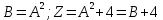
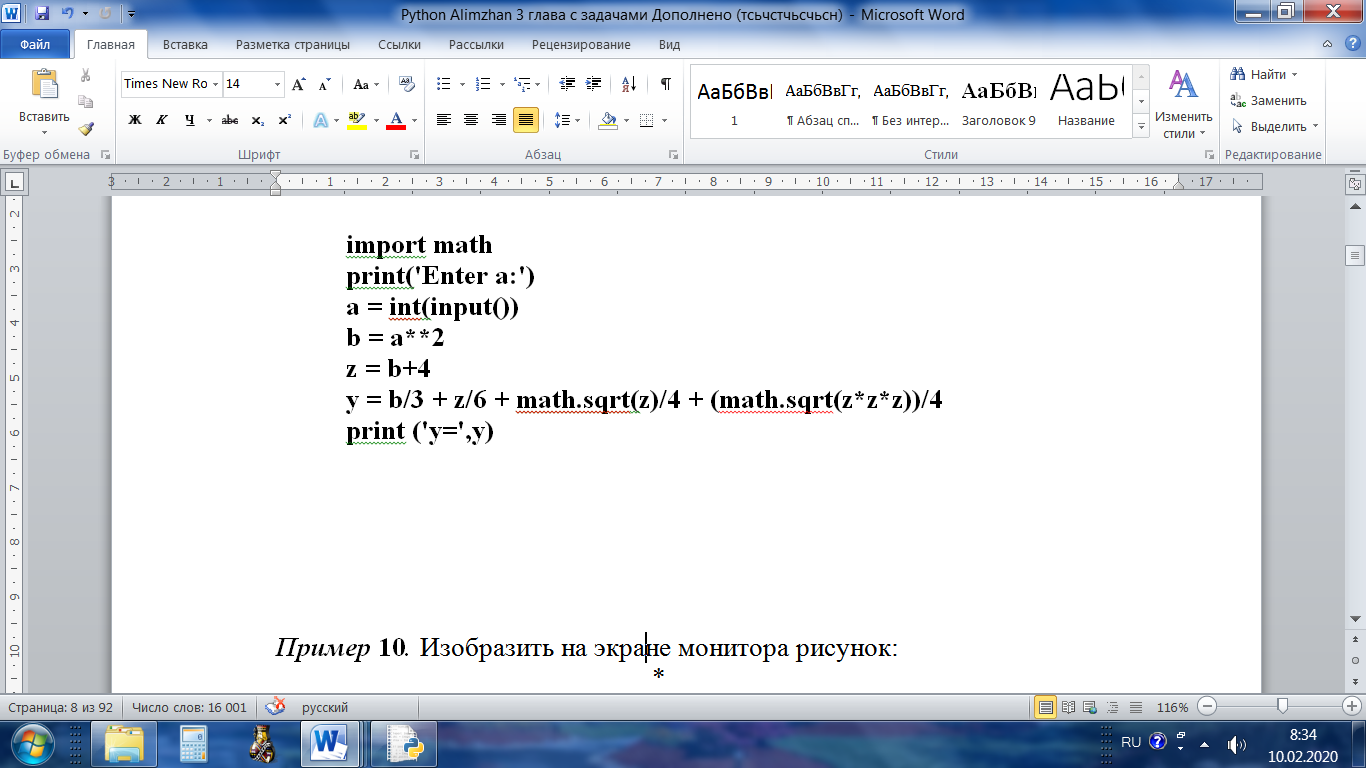
Пример 3. Перестановка цифр двузначного числа
Пусть дано n=25.
x1:= 25 % 10 = 5
x2:= 25 // 10=2
m:=5*10+2 = 52, что требуется получить.
print ('Введите двузначное число: ')
n = input()
x1 = n%10
x2 = n//10
m = x1*10+x2
print (m)
Пример 12. Дано вещественное число А, содержащее два знака до запятой и два после. Получить новое число, поменяв в числе А целую и дробную части.
Попробуем найти целую и дробную части числа. А потом просто соберем новое число, увеличив дробную часть в 100 раз и уменьшив целую часть тоже в 100 раз.
# Обмен дробной и целой частей числа
import math
print ('Введите число: ')
a = float(input())
x1 = int(a)
x2 = a%1
b = x1/100+x2*100
print (b)
Составьте алгоритм в виде блок-схемы и запишите в тетрадь
Задания на самостоятельную работу:
Вычислите функцию по Вариантам:
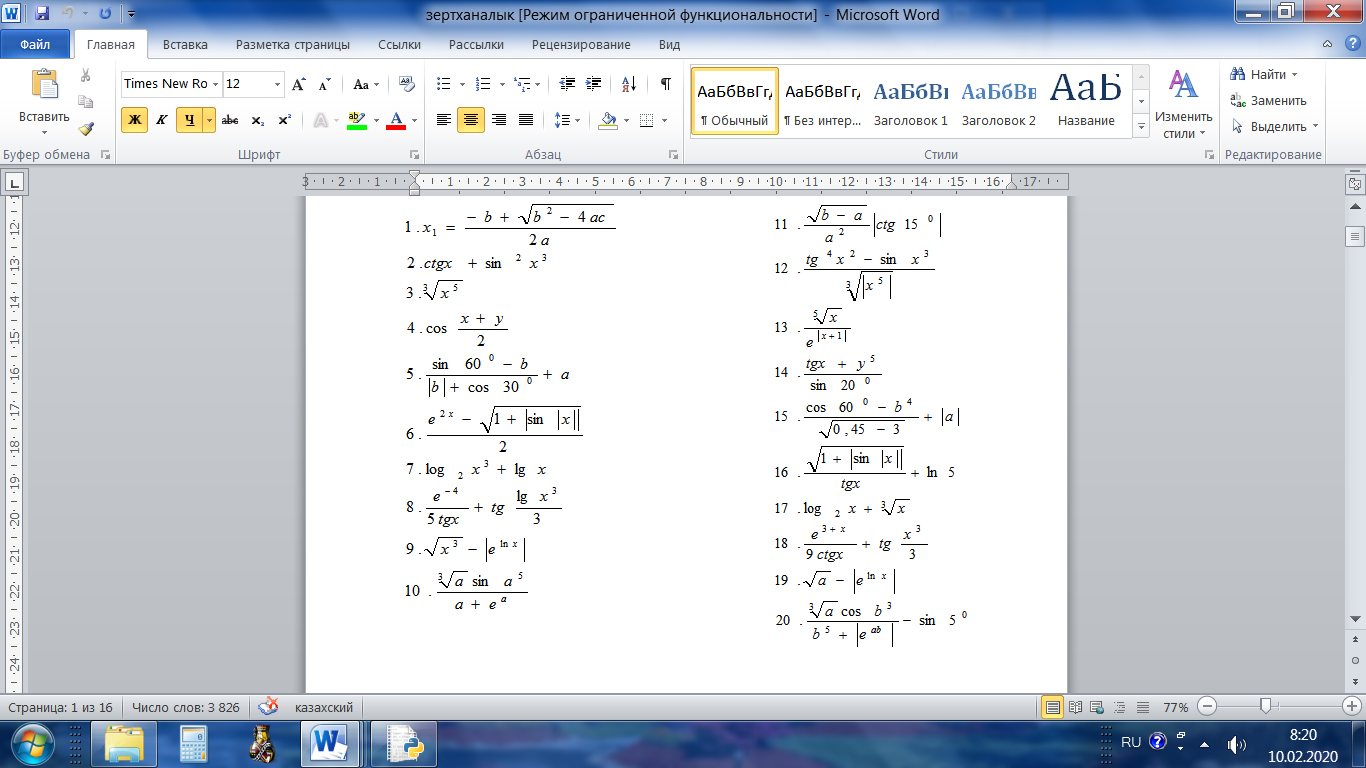
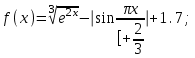
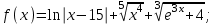
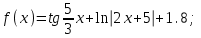
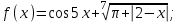
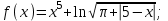
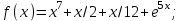
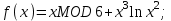
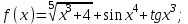
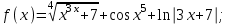
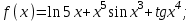
Вопросы и задания
Какие величины называются переменными, постоянными? Приведите примеры.
Какие величины называются аргументами, результатами алгоритма?
Запишите общий вид алгоритма.
Какие типы величин используются в языке программирования Python?
Чем характеризуются переменные величины?
Какие имена переменных можно использовать в Python?
Для чего необходимо описывать данные в программах?
Какой оператор используется для ввода данных?
Как перевести курсор на новую строку после ввода данных?
Как вывести результаты работы программы на экран?
Каким образом можно вывести результаты с новой строки?
Как удержать результаты вывода на экране дисплея после срабатывания оператора print?
Какое значение будет присвоено переменным M и N после серии команд:
а) М:=0; М:=М+2; М:=3*М; М:=М-2; М:=М*М;
б) N:=1; N:= N+1; N:= N* N; N:= N2.
В трех сосудах содержится вода. В первом сосуде V1 л воды температуры t1, во втором – V2 л температуры t2, в третьем – V3 л температуры t3. Воду слили в один сосуд. Составить программу для определения объема V и температуры Т воды в этом сосуде (расчет температуры можно вести по упрощенной формуле: Т=(t1+t2+t3)/3).
Вычислить радиус RB вписанной и радиус RO описанной около треугольника окружности, если заданы стороны треугольника А, В, С.
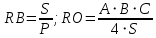 , ,
где S - площадь, Р - полупериметр треугольника.
Какой результат отобразится на экране после выполнения фрагмента программы на Python?
k=4;
print (‘данные’)
a=k+10;
k=k+a;
print (a, k, k*k, a*a)
print (‘результат:’,’a=’,a,’k=’,k);
* Восстановить текст программы по имеющейся информации:
память компьютера экран
  S – F = 78
F – D = 19
S * D = 300

* Написать программу для определения высоты Н, радиуса RB вписанной и радиуса RO описанной окружности, площади треугольника, заданного координатами своих вершин X1, Y1, X2, Y2, X3, Y3. Стороны треугольника А, В, С определяются формулами:
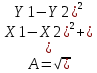 ; ; 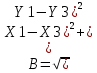 ; ;
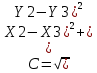
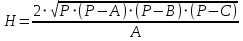 ; ; 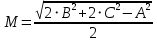 , где , где 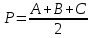
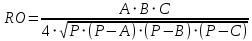 ; ; 
*Составить программу для отгадывания с помощью компьютера задуманного числа. Компьютер предлагает исполнителю произвести следующие действия и ввести результат:
а) умножить задуманное число на 5;
б) прибавить 8;
в) сумму умножить на 2.
По введенному результату компьютер определяет число и печатает его на экране.
*Поменять местами значения переменных X и Y, не используя дополнительной переменной.
*Дано трехзначное число.
Найти:
a) Число единиц в нем; b) Число десятков в нем;
c) Сумму его цифр; d) Произведение его цифр.
*Дано трехзначное число. В нем зачеркнули последнюю справа цифру и приписали ее вначале. Найти полученное число
*Дано целое число k (1 <= k <= 365). Присвоить целочисленной величине n значение 1, 2, ..., 6 или 0 в зависимости от того, на какой день недели (понедельник, вторник, ..., суббота или воскресенье) приходится k-й день года, в котором 1 января – понедельник.
|
 Скачать 0.73 Mb.
Скачать 0.73 Mb.