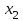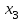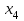ММИ2 24В. Практическая работа 2 Решение системы линейных алгебраических уравнений методом Зейделя
 Скачать 65.19 Kb. Скачать 65.19 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования «КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ЭНЕРЕГЕТИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра: «Инженерная графика» Практическая работа №2 «Решение системы линейных алгебраических уравнений методом Зейделя» Дисциплина: «Методы моделирования и исследования» Работу выполнил: Студент группы ЗПТ-1-19 Северьянова Л.Н. Руководитель: Гимадиев Р.Ш. Казань 2021 Введение Снова рассмотрим систему уравнений с работы №1. Дана система уравнений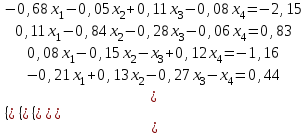 (2.0) (2.0) В матричном виде 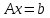 , (2.1) , (2.1)Теорема. Для существования единственного решения системы (2.1) и сходимости метода Зейделя достаточно выполнения хотя бы одного из двух условий: a) 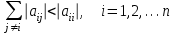 b) Хотя бы одна из норм матрица 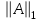 или или 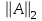 (определенные по работе №1) меньше единицы. (определенные по работе №1) меньше единицы.Проверяем систему (2.0): Для первой и последующих строк  ; ;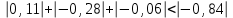 ; ;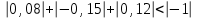 ; ;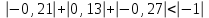 . .Следовательно, система уравнений (2.0) сходится по требованиям работы №1, также эта система должна сходится в соответствии теоремы Зейделя. Расмотрим алгоритм решения системы уравнения по Зейделю. Пусть у системы уравнений (2.1) матрица 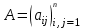 и все диагональные элементы и все диагональные элементы  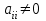 , , 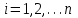 . Если . Если 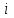 -ое уравнение (2.1) разделить на -ое уравнение (2.1) разделить на 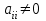 , затем все неизвестные кроме , затем все неизвестные кроме 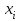 перенести вправо, то эквивалентное уравнение имеет вид: перенести вправо, то эквивалентное уравнение имеет вид: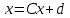 , (2.2) , (2.2) где 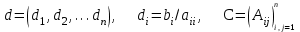 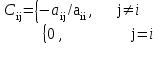 Метод Зейделя состоит в том, что итерации производятся по формуле 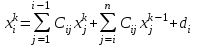 , (2.3) , (2.3)где 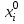 - произвольный набор начальных данных, - произвольный набор начальных данных, 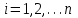 , , 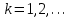 Итерации (2.3) по методу Зейделя отличаются от простых итераций тем, что при нахождении 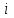 -й компоненты -й компоненты 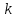 -го приближения сразу используются уже найденные компоненты -го приближения сразу используются уже найденные компоненты 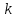 -го приближения с меньшими номерами. -го приближения с меньшими номерами. Замечание, варианты для выполнения задания удовлетворяют требованиям теоремы Зейделя и сразу можно перейти к алгоритму решения (2.3) Сложности возникают в случае, если система уравнений не удовлетворяет требованиям теоремы Зейделя. Рабочее задание. 24 Вариант.  Методом Зейделя решить эту систему уравнений с точностью 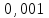 , приведя ее к виду, удобному для итераций. Приведем систему к виду, в котором все диагональные элементы превосходили бы остальные элементы строк. , приведя ее к виду, удобному для итераций. Приведем систему к виду, в котором все диагональные элементы превосходили бы остальные элементы строк.Теорема. Для существования единственного решения системы (2.1) и сходимости метода Зейделя достаточно выполнения хотя бы одного из двух условий: a) 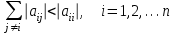 b) Хотя бы одна из норм матрица 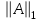 или или 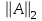 (определенные по работе №1) меньше единицы. (определенные по работе №1) меньше единицы.Проверяем систему: Для первой и последующих строк 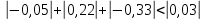 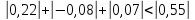 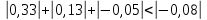 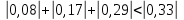 Условие (а) не выполняется. Проверим условие (б): ‖С ‖=max{0,63;0,92;0,59;0,87}=0,92<1 Условие сходимости (б) выполняется. И так, расчет ведется по следующей процедуре 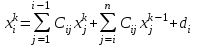 Итерации (2.3) по методу Зейделя отличаются от простых итераций тем, что при нахождении -й компоненты -го приближения сразу используются уже найденные компоненты -го приближения с меньшими номерами. 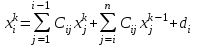 При k=0  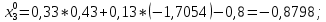  Таблица
Сходимость в тысячных долях имеет место уже при k=10. В методе простых итераций сходимость наблюдается при k=11 Вывод: метод Зейделя позволяет сократить число итераций. Ответ:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||