Практическая работа 3,4. Практическая работа 3 Название практической работы Перевод целых чисел из одной системы счисления в другую

• Название: Практическая работа 3 Название практической работы Перевод целых чисел из одной системы счисления в другую
• Дата: 12.02.2021
• Размер: 277.06 Kb.
• Имя файла: Практическая работа 3,4.docx
• Тип: Практическая работа; #175971

Практическая работа №3

Название практической работы: Перевод целых чисел из одной системы счисления в другую.

Цель работы: научиться записывать числа в развернутой форме, переводить числа из одной системы счисления в другую.

Теоретический материал:

Система счисления — это способ представления любого числа с помощью алфавита символов, называемых цифрами. Системы счисления делятся на позиционные и непозиционные. В позиционных системах любое число записывается в виде последовательности цифр, количественное значение которых зависит от места (позиции), занимаемой каждой из них в числе. Примеры: десятичная, восьмеричная, двоичная система и т.д.

Развёрнутая форма записи числа:

А_n = a_n-1 q ^n-1 + a_n-2 q ^n-2 + ... + a₁ q¹ + a₀ q⁰ + a_-1 q^-1 + ... + a_-m q^-m,

где a_i — цифры системы счисления;

n и m — число целых и дробных разрядов, соответственно.

Например,

456,25₁₀ = 4  10² + 5  10¹ + 6  10⁰ + 2  10^-1 + 5 10^-2

Любая позиционная система счисления характеризуется своим основанием.

Основание позиционной системы счисления — количество различных цифр, используемых для изображения чисел в данной системе счисления.

Система счисления				Система счисления
10-ая	2-ая	8-ая	16-ая	10-ая	2-ая	8-ая	16-ая
0	00	00	00	9	1001	11	09
1	01	01	01	10	1010	12	A
2	10	02	02	11	1011	13	B
3	11	03	03	12	1100	14	C
4	100	04	04	13	1101	15	D
5	101	05	05	14	1110	16	E
6	110	06	06	15	1111	17	F
7	111	07	07	16	10000	21	10
8	1000	10	08

Пример№1: Перевести число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную: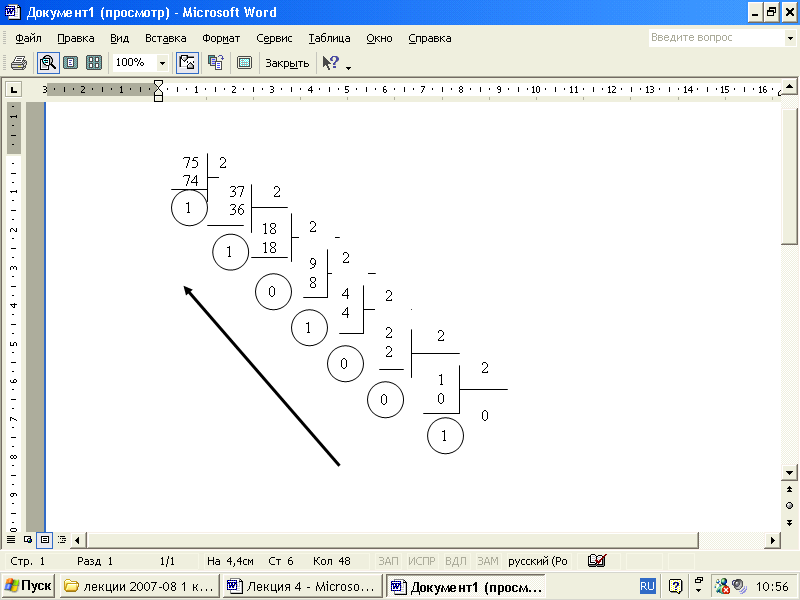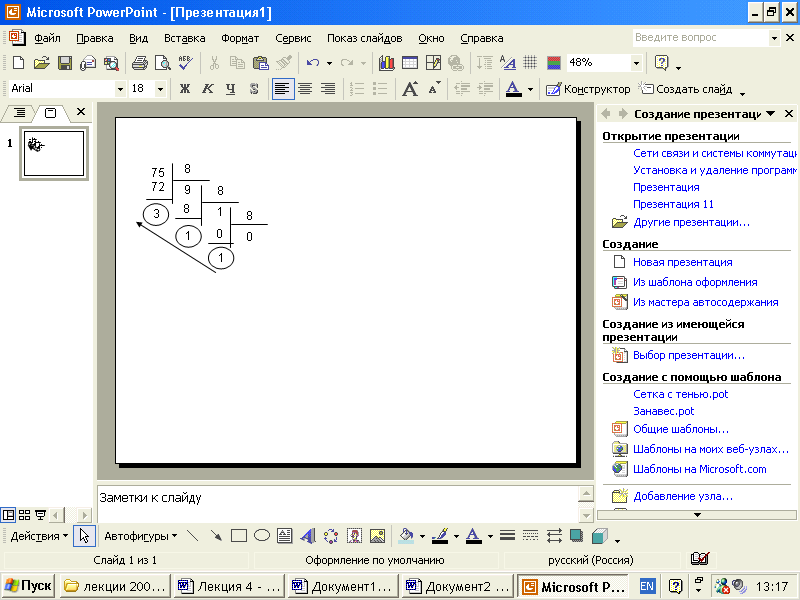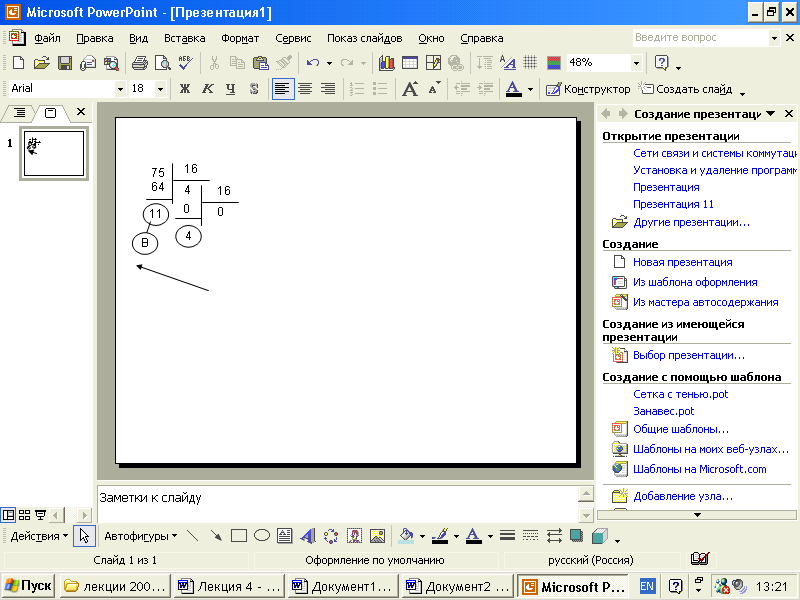


Ответ: 75₁₀ = 1 001 011₂   =  113₈  =  4B₁₆
Алгоритм перевода целых чисел из системы с основанием р в систему с основанием q:

1. 
   Основание новой системы счисления выразить цифрами исходной системы счисления и все последующие действия производить в исходной системе счисления.
   
2. 
   Последовательно выполнять деление данного числа и получаемых целых частных на основании новой системы счисления до тех пор, пока не получим частное меньше делителя.
   
3. 
   Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствии с алфавитом новой системы счисления.
   
4. 
   Составить число в новой системе счисления, записывая его, начиная с последнего остатка.
   

Например, 10011₂ = 1*2⁴ + 0*2³ + 0*2² + 1*2¹ + 1*2⁰ = 16 + 2 + 1 =19₁₀
При переводе числа из двоичной системы счисления в восьмеричную нужно сгруппировать по 3 цифры (триады), начиная с младшего разряда, затем заменить каждую группу разрядов соответствующей цифрой восьмеричной системы счисления. Например, 10110₂= 010 110=26₈,

При переводе числа из двоичной системы счисления в шестнадцатеричную нужно сгруппировать справа налево разряды по 4 цифры (тетрады), затем заменить каждую группу разрядов соответствующей цифрой шестнадцатеричной системы счисления. Например, 1011100₂= 01011100=5C₁₆
Ход работы:

1. 
   Запишите развернутую форму числа:
   

а). 88₁₀;

б). 11000001110₂;

в). 35₈;

г). 5СВ₁₆;

2. 
   Используя метод последовательного деления, переведите числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную системы счисления:
   

1. 
   125₁₀ = ____₂;
   
2. 
   88₁₀ = ____₂;
   
3. 
   95₁₀ = ____₂ =_____₈ = _____₁₆;
   
4. 
   240₁₀ = ____₂ =____₈ = ____₁₆;
   

3. 
   Переведите восьмеричное число в двоичную и шестнадцатеричную системы счисления:
   

1. 
   43₈ = ____₂ = ____₁₆;
   
2. 
   71₈ = ____₂ = ____₁₆;
   
3. 
   1005₈ = ____₂ = ____₁₆;
   
4. 
   56₈ = ______₂ = ____₁₆;
   

4. 
   Переведите шестнадцатеричное число в двоичную и восьмеричную системы счисления:
   

1. 
   65D₁₆ = ____₂ = _____₈;
   
2. 
   12A1₁₆ = ____₂ = _____₈;
   
3. 
   FF70₁₆ = ____₂= _____₈.
   

5. 
   Переведите числа из двоичной системы в десятичную систему счисления:
   

CC 2	CC 10		CC 2	CC 10
11101010111012			10111001001112
101111011112			11000101110012

6. 
   Выполните перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную системы счисления:
   

1. 
   110111010101100₂ = _______₈;
   
2. 
   101010111011110₂ = _______₁₆;
   
3. 
   1010110000001₂ = _______₈;
   
4. 
   11111000110010₂ = ________₁₆.
   

7. 
   Переведите шестнадцатеричное число в двоичную и восьмеричную системы счисления:
   

1. 
   2СE₁₆= _______₂ = ________8;
   
2. 
   9F40₁₆= _______₂ = ________8;
   
3. 
   ABCDE₁₆= _______₂ = ________8;
   
4. 
   10101₁₆= _______₂ = ________8;
   
5. 
   1A9D₁₆ = _______₂ = ________8.
   

8. 
   Полученные результаты занесите в итоговую таблицу.
   
9. 
   Ответьте на контрольные вопросы:
   

• 
  Дайте определение основанию системы счисления;
  
• 
  Запишите алгоритм перевода из двоичной системы счисления в восьмеричную.
  

10. 
    Оформите и сдайте отчет преподавателю.
    

Практическая работа №4

Название практической работы: Перевод смешанных чисел, содержащих целую и дробную части

Цель работы: научиться переводить смешанные числа в различные системы счисления, выполнять арифметические действия над смешанными числами.

Теоретический материал:

Для перевода смешанной дроби из одной системы счисления в другую необходимо:

• 
  Представить эту дробь в виде суммы целого числа и десятичной дроби, а затем произвести перевод каждой части отдельно по соответствующим правилам.
  

Например, перевести 25,25₁₀ в двоичную систему счисления.

1. 
   Переводим целую часть 25₁₀=11001₂
   
2. 
   Затем – дробную: эту дробь умножить на 2, затем дробную часть, полученного произведения вновь умножить на 2 и так до тех пор, пока в дробной ч 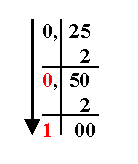асти не окажутся все нули, либо не будет достигнута заданная степень точности. Целые части, полученных произведений взятые по схеме сверху вниз, и дадут результат перевода.
   
3. 
   Соединим целую и дробную части и получили: 25,250010=11001,01₂
   

Пример №1: Перевести десятичную дробь 0,1875 в двоичную, восьмеричную и шестнадцатеричную системы.



Здесь вертикальная черта отделяет целые части чисел от дробных частей.
Отсюда: 0,1875₁₀=0,0011₂=0,14₈=0,3₁₆
Двоичная арифметика

Сложение двоичных чисел

Способ сложения столбиком такой же, как и для десятичного числа. То есть, сложение выполняется поразрядно, начиная с младшей цифры. Если получается больше 1, то записывается 1 и 1 добавляется к старшему разряду (говорят «на ум пошло»).

Выполним пример: 10011 + 10001.

	1	0	0	1	1
	1	0	0	0	1
1	0	0	1	0	0

Первый разряд: 1+1 = 2. Записываем 0 и 1 на ум пошло.

Второй разряд: 1+0+1(запомненная единица) =2. Записываем 0 и 1 на ум пошло.

Третий разряд: 0+0+1(запомненная единица) = 1. Записываем 1.

Четвертый разряд 0+0=0. Записываем 0.

Пятый разряд 1+1=2. Записываем 0 и добавляем к шестым разрядом 1.

Переведём все три числа в десятичную систему и проверим правильность сложения.

10011 = 1*2⁴ + 0*2³ + 0*2² + 1*2¹ + 1*2⁰ = 16 + 2 + 1 =19

10001 = 1*2⁴ + 0*2³ + 0*2² + 0*2¹ + 1*2⁰ = 16 + 1 = 17

100100 = 1*2⁵ + 0*2⁴ + 0*2³ + 1*2² + 0*2¹ + 0*2⁰ =32+4=36

17 + 19 = 36 верное равенство

Таблица сложения в двоичной системе счисления:

+	0	1
0	0	1
1	1	10

Вычитание двоичных чисел

Вычитать числа нужно также столбиком и общее правило тоже, что и для десятичных чисел, вычитание выполняется поразрядно и если в разряде не хватает единицы, то она занимается в старшем. Решим следующий пример:

	1	1	0	1
-		1	1	0
		1	1	1

Первый разряд. 1 - 0 =1. Записываем 1.

Второй разряд 0 -1. Не хватает единицы. Занимаем её в старшем разряде. Единица из старшего разряда переходит в младший, как две единицы (потому что старший разряд представляется двойкой большей степени ) 2-1 =1. Записываем 1.

Третий разряд. Единицу этого разряда мы занимали, поэтому сейчас в разряде 0 и есть необходимость занять единицу старшего разряда. 2-1 =1. Записываем 1.

Проверим результат в десятичной системе

1101 - 110 = 13 - 6 = 7 (111) Верное равенство.
Умножение в двоичной системе счисления.

Любое двоичное число разлагается по степеням двойки, то становится ясно, что умножение в двоичной системе счисления сводится к умножению на 10 (то есть на десятичную 2), а стало быть, умножение это ряд последовательных сдвигов. Общее правило таково: как и для десятичных чисел, умножение двоичных выполняется поразрядно. И для каждого разряда второго множителя к первому множителю добавляется один ноль справа.

Пример (пока не столбиком):1011 * 101

Это умножение можно свести к сумме трёх поразрядных умножений:

1011 * 1 + 1011 * 0 + 1011 * 100 = 1011 +101100 = 110111

В столбик это же самое можно записать так: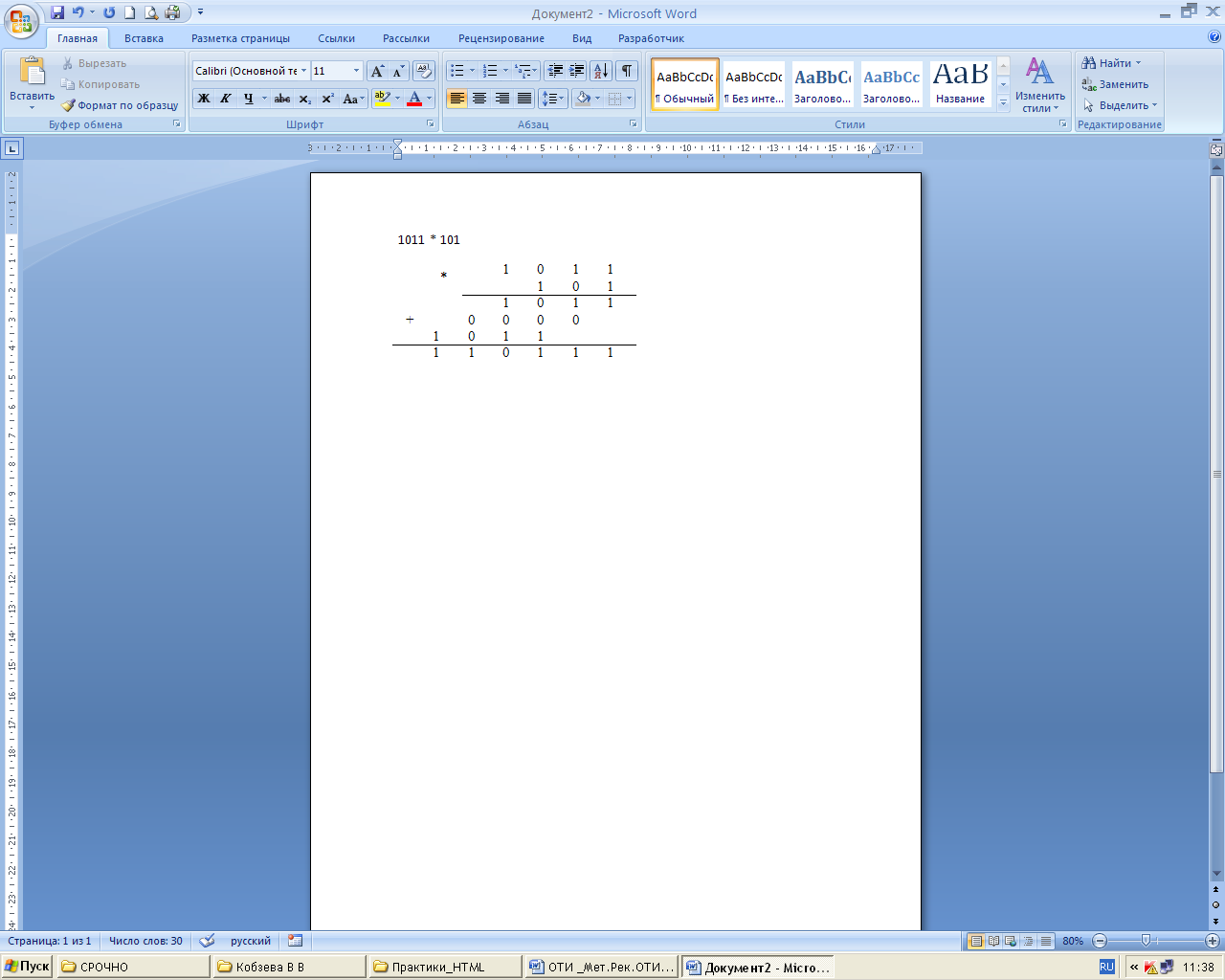


Проверка:

101 = 5 (десятичное)

1011 = 11 (десятичное)

110111 = 55 (десятичное)

5*11 = 55 верное равенство

Таблица умножения в двоичной системе счисления:

*	0	1
0	0	0
1	0	1

Ход работы:

1. 
   Укажите минимальное основание системы счисления, если в ней можно записать числа: 341, 123, 111, 222 - …
   
2. 
   Переведите целые числа из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления:
   

1. 
   231₁₀  =_____;
   
2. 
   564₁₀  =_____;   
   
3. 
   1023₁₀  =____;      
   
4. 
   4096₁₀ =____.
   

3. 
   Переведите в десятичную систему счисления:
   

1. 
   10011101₂ =____________;
   
2. 
   110010100110₂=________;
   
3. 
   101111001101111₂ =_____.
   
4. 
   321₈ = ______;
   
5. 
   2367₈ = _____;
   
6. 
   53621₈ = ____;
   
7. 
   3А₁₆ = ______;
   
8. 
   В14₁₆= _____;
   
9. 
   4А4С₁₆ = ____;
   
10. 
    А55DD ₁₆ = __.
    

4. 
   Переведите десятичные дроби в двоичную, восьмеричную и шестнадцатеричную системы счисления:
   

1. 
   0,5₁₀  =______;
   
2. 
   0,125₁₀  =____;    
   
3. 
   0,654₁₀  =____.      
   

5. 
   Переведите смешанные десятичные числа в двоичную, восьмеричную и шестнадцатеричную системы счисления, оставив пять знаков в дробной части нового числа:
   

1. 
   21,5₁₀  =______;
   
2. 
   432,54₁₀  =____;    
   
3. 
   678,333₁₀  =____.  
   

6. 
   Сложите, вычтите, умножьте и разделите двоичные числа
   11010101₂ и 1110₂.
   
7. 
   Выполните арифметические операции:
   

1. 
   1100000011,011₂ * 101010111,1₂;
   
2. 
   1510,2₈ – 1230,54₈;
   
3. 
   3B3,8₁₆+38B,4₁₆.
   

8. 
   Переведите смешанные восьмеричные числа в двоичную систему счисления:
   

1. 
   721, 61₈ = _______;
   
2. 
   324, 65₈ = _______;
   
3. 
   123,50 = ________;
   
4. 
   231,76 = ________.
   

9. 
   Переведите смешанные шестнадцатеричные числа в двоичную и восьмеричную систему счисления:
   

1. 
   A16, 8F₁₆ = ______;
   
2. 
   C14, 8D₁₆ = ______;
   
3. 
   221,99₁₆ = _______;
   
4. 
   450,А1₁₆ = _______.
   

10. 
    Выполните арифметические операции (в двоичной системе счисления):
    

1. 
   110011,011₂+ 1010111,111₂;
   
2. 
   10,7₈* 30,46₈;
   
3. 
   BA,9₁₆* D1,8₁₆.
   

11. 
    Полученные результаты занесите в итоговую таблицу.
    
12. 
    Ответьте на контрольные вопросы:
    

• 
  Запишите таблицу сложения двоичных чисел;
  
• 
  Запишите алгоритм перевода смешанной дроби из одной системы счисления в другую.
  

13. 
    Оформите и сдайте отчет преподавателю.