Практическая работа 3. Openmp редукция

Название	Практическая работа 3. Openmp редукция
Дата	05.04.2023
Размер	0.64 Mb.
Формат файла
Имя файла	Savinova_PMIb-1902_pr3.docx
Тип	Практическая работа #1040368

Савинова Е.А. ПМИб-1902а

Практическая работа №3. OpenMP - редукция.

Цель работы: углубить знания в разработке параллельных итерационных алгоритмов,приобрести умение разрабатывать параллельные итерационные алгоритмы, развить навыки программирования алгоритмов на С++.

Задание

Напишите программу, вычисляющую значение определённого интервала по параллельному итерационному алгоритму методом трапеций и методом Симпсона. На входе программы – число интервалов.

Условия:

Определите точность решения задачи на тестовых примерах при использовании метода трапеций и метода Симпсона при одинаковом количестве интервалов;
Проведите анализ эффективности решения параллельной задачи в случае метода трапеции. Постройте график, объясните полученные результаты.

Код программы:

double iterTrap(const double a, const double b, const int dlin, double f(double), int k)

{

double wtime = omp_get_wtime();

double left = 0.0, right = 0.0, sum = 0.0;

const double step = (b - a) / dlin;

left = f(a);

# pragma omp parallel for private( right , left ) reduction (+: sum) num_threads(k)

for (int i = 1; i < dlin; i++)

{

right = f(a + step * i);

left = f(a + step * (i - 1));

sum += ((left + right) * step) / 2;

left = right;

}

fout << dlin << "\t" << k << "\t" << omp_get_wtime() - wtime << "\n";

return sum;

}

double simpson_integral(double a, double b, int dlin, double f(double), int k)

{

double wtime = omp_get_wtime();

const double step = (b - a) / dlin;

double k1 = 0, k2 = 0;

# pragma omp parallel for reduction (+: k1,k2) num_threads(k)

for (int i = 1; i < dlin; i += 2)

{

k1 += f(a + i * step);

k2 += f(a + (i + 1) * step);

}

fsout << dlin << "\t" << k << "\t" << omp_get_wtime() - wtime << "\n";

return step / 3 * (f(a) + 4 * k1 + 2 * k2);

}
double func(double a)

{

double x = ((sqrt(a) + 2.0) / sqrt(a));

return x;

}

int main()

{

double a = 4.0, b = 16.0;

for (int i = 1; i <= 10; i++)

{

setlocale(LC_ALL, "Russian");

cout << i << "потока" << "\n";

cout << setprecision(numeric_limits::digits10 + 1) << iterTrap(a, b, 100000, func, i) << endl;

cout << setprecision(numeric_limits::digits10 + 1) << iterTrap(a, b, 500000, func, i) << endl;

cout << setprecision(numeric_limits::digits10 + 1) << iterTrap(a, b, 1000000, func, i) << endl;

cout << setprecision(numeric_limits::digits10 + 1) << iterTrap(a, b, 5000000, func, i) << endl;

cout << setprecision(numeric_limits::digits10 + 1) << iterTrap(a, b, 10000000, func, i) << endl;

cout << setprecision(numeric_limits::digits10 + 1) << simpson_integral(a, b, 100000, func, i) << endl;

cout << setprecision(numeric_limits::digits10 + 1) << simpson_integral(a, b, 500000, func, i) << endl;

cout << setprecision(numeric_limits::digits10 + 1) << simpson_integral(a, b, 1000000, func, i) << endl;

cout << setprecision(numeric_limits::digits10 + 1) << simpson_integral(a, b, 5000000, func, i) << endl;

cout << setprecision(numeric_limits::digits10 + 1) << simpson_integral(a, b, 100000000, func, i) << endl;

}

}

Результат выполнения программы представлен на рисунке 1.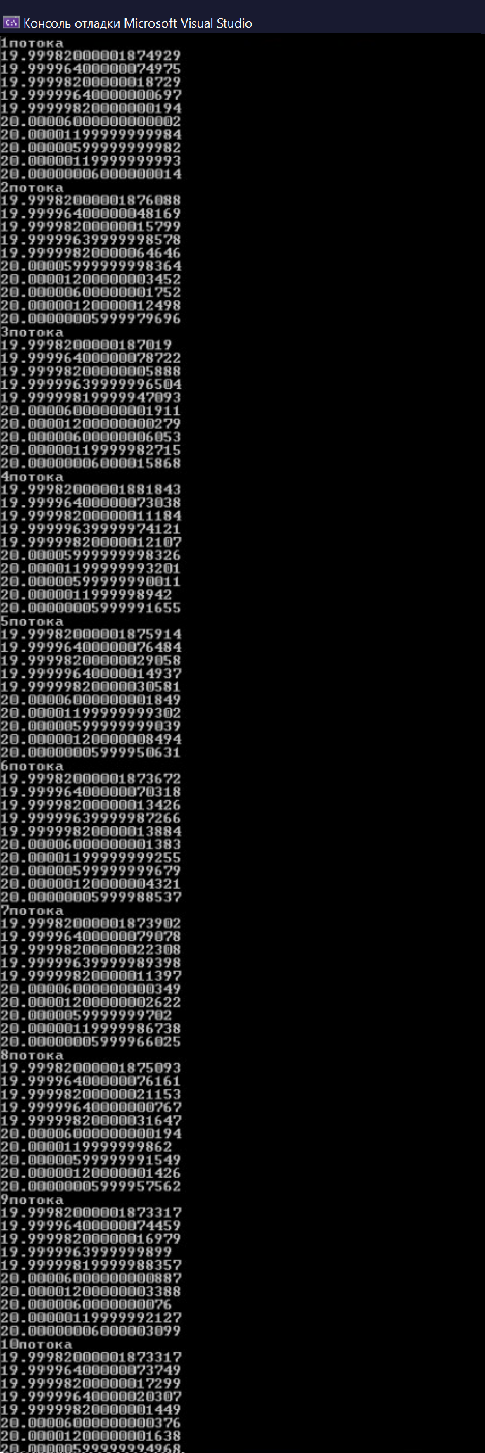

Рисунок 1 - Результат выполнения программного кода вычисляющую значение определённого интервала по параллельному итерационному алгоритму методом трапеций и методом Симпсона

На рисунке 2 представлена диаграмма анализа эффективности решения параллельной задачи в случае метода трапеции.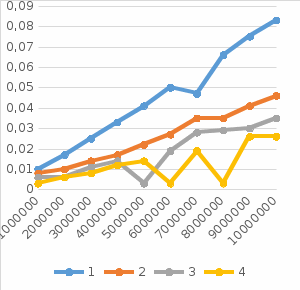

Рисунке 2 - Диаграмма анализа эффективности решения параллельной задачи в случае метода трапеции

Чем больше интервалов, тем больше требуется времени, а чем больше потоков, тем меньше времени.

Используя программу задания 1, вычислите значение числа :

а) по правому верхнему квадранту единичной окружности;

б) как значение

Условие:

оцените точность вычислений в зависимости от числа интервалов.

Код программы:

double funcb(double a)

{

double x = 4 / (1 + pow(a, 2));

return x;

}

double pi(double a)

{

double x = sqrt(1 - pow(a, 2));

return x * 4;

}

#include

#include

#include

#include

#include

#include

#define double long double

using namespace std;

ofstream fout("tabtrap.txt", ios_base::trunc);

ofstream fsout("tabsimp.txt", ios_base::trunc);

double func(double a)

{

double x = ((sqrt(a) + 2.0) / sqrt(a));

return x;

}

double funcb(double a)

{

double x = 4 / (1 + pow(a, 2));

return x;

}

double pi(double a)

{

double x = sqrt(1 - pow(a, 2));

return x * 4;

}

double iterTrap(const double a, const double b, const int dlin, double f(double), int k)

{

double wtime = omp_get_wtime();

double left = 0.0, right = 0.0, sum = 0.0;

const double step = (b - a) / dlin;

left = f(a);

# pragma omp parallel for private( right , left ) reduction (+: sum) num_threads(k)

for (int i = 1; i < dlin; i++)

{

right = f(a + step * i);

left = f(a + step * (i - 1));

sum += ((left + right) * step) / 2;

left = right;

}

fout << dlin << "\t" << k << "\t" << omp_get_wtime() - wtime << "\n";

return sum;

}

double simpson_integral(double a, double b, int dlin, double f(double), int k)

{

double wtime = omp_get_wtime();

const double step = (b - a) / dlin;

double k1 = 0, k2 = 0;

# pragma omp parallel for reduction (+: k1,k2) num_threads(k)

for (int i = 1; i < dlin; i += 2)

{

k1 += f(a + i * step);

k2 += f(a + (i + 1) * step);

}

fsout << dlin << "\t" << k << "\t" << omp_get_wtime() - wtime << "\n";

return step / 3 * (f(a) + 4 * k1 + 2 * k2);

}

int main()

{

double a = 4.0, b = 16.0;

for (int i = 1; i <= 10; i++)

{

setlocale(LC_ALL, "Russian");

cout << i << "потока" << "\n";

cout << setprecision(numeric_limits::digits10 + 1) << iterTrap(a, b, 100000, func, i) << endl;

cout << setprecision(numeric_limits::digits10 + 1) << iterTrap(a, b, 500000, func, i) << endl;

cout << setprecision(numeric_limits::digits10 + 1) << iterTrap(a, b, 1000000, func, i) << endl;

cout << setprecision(numeric_limits::digits10 + 1) << iterTrap(a, b, 5000000, func, i) << endl;

cout << setprecision(numeric_limits::digits10 + 1) << iterTrap(a, b, 10000000, func, i) << endl;

cout << setprecision(numeric_limits::digits10 + 1) << simpson_integral(a, b, 100000, func, i) << endl;

cout << setprecision(numeric_limits::digits10 + 1) << simpson_integral(a, b, 500000, func, i) << endl;

cout << setprecision(numeric_limits::digits10 + 1) << simpson_integral(a, b, 1000000, func, i) << endl;

cout << setprecision(numeric_limits::digits10 + 1) << simpson_integral(a, b, 5000000, func, i) << endl;

cout << setprecision(numeric_limits::digits10 + 1) << simpson_integral(a, b, 100000000, func, i) << endl;

}

cout << setprecision(numeric_limits::digits10 + 1) << simpson_integral(0, 1, 100000, pi, 4) << "\n";

cout << setprecision(numeric_limits::digits10 + 1) << iterTrap(0, 1, 100000, pi, 4) << "\n";

cout << setprecision(numeric_limits::digits10 + 1) << simpson_integral(0, 1, 100000, funcb, 4) << "\n";

cout << setprecision(numeric_limits::digits10 + 1) << iterTrap(0, 1, 100000, funcb, 4) << "\n";

return 0;

}

Результат выполнения программы представлен на рисунке 3.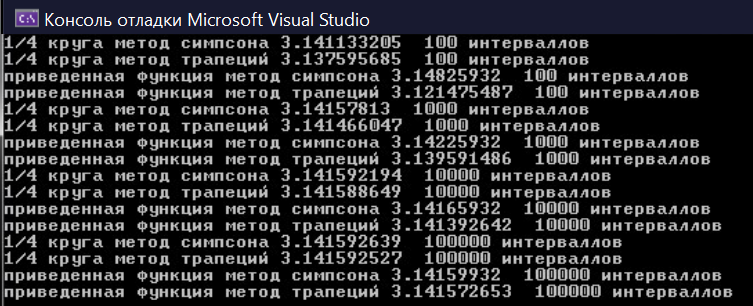

Рисунок 3 - Результат выполнения программного кода

Чем больше интервалов , тем точнее вычисления.

Используя примеры 39.1с и 39.2с из http://openmp.org/mpdocuments/OpenMP_Examples_4.0.1.pdf, страница 140, напишите параллельную программу для вычисления минимума и максимума в массиве.

Код программы:

#include

#include

#include

#include

#include

#include

using namespace std;

int main()

{

setlocale(LC_ALL, "Russian");

srand(time(0));

int arr[10], i;

for (i = 0; i < 10; i++) {

arr[i] = rand() % 100;

cout << arr[i] << " ";

}

cout << "\n";

int max_val, min_val = arr[i];

#pragma omp parallel for reduction(max : max_val)reduction(min : min_val) num_threads(4)

for (i = 0; i < 10; i++)

{

if (arr[i] > max_val)

{

max_val = arr[i];

}

if (arr[i] < min_val)

{

min_val = arr[i];

}

}

cout << "первый метод\n";

cout << max_val << "\n";

cout << min_val << "\n";

cout << "второй метод\n";

max_val = 0;

min_val = 0;

#pragma omp parallel shared( max_val, min_val)

#pragma omp for private(i)

for (i = 0; i < 10; i++)

{

if (arr[i] > max_val)

{

#pragma omp critical

max_val = arr[i];

}

if (arr[i] < min_val)

{

#pragma omp critical

min_val = arr[i];

}

}

cout << max_val << "\n";

cout << min_val << "\n";

return 0;

}

На рисунке 4 представлен результат выполнения параллельной программы для вычисления минимума и максимума в массиве.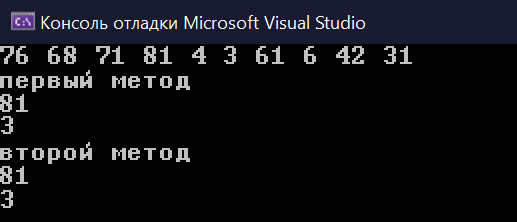

Рисунок 4 - Результат выполнения программного кода для вычисления минимума и максимума в массиве

Вывод: Были получены углубить знания в разработке параллельных итерационных алгоритмов,приобретены умение разрабатывать параллельные итерационные алгоритмы, развиты навыки программирования алгоритмов на С++.