опрос. Практическая работа_3. Практическая работа 3. Расчет электрической цепи с двумя источниками
 Скачать 141 Kb.
|
Практическая работа №3. «Расчет электрической цепи с двумя источниками»Цель работыНаучиться проводить расчеты в разветвленной электрической цепи постоянного тока с двумя источниками ЭДС. 1.Теоретические сведенияЗаконы Кирхгофа Линейным называется элемент цепи, сопротивление которого остается постоянным независимо от значения и направления тока в нем и напряжения на его выводах. Электрическая цепь называется линейной, если она содержит только линейные элементы. Ветвью электрической цепи называется её участок, состоящий из одного или нескольких элементов, по которым проходит один и тот же ток. Такое соединение элементов называется последовательным. Например, ветвь, состоящая из одного источника питания с ЭДС Е, внутренним сопротивлением r0 и резистора с сопротивлением R, показана на рисуноке 3.1. Остальные участки цепи на этом рисунке не показаны. 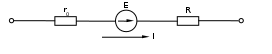 Рисунок 3.1. Ветвь электрической цепи Точка электрической цепи называется узлом (точкой разветвления), если в ней соединены три или большее число ветвей. На рисуноке 3.2. показана часть схемы замещения цепи и её четыре узла (А, Б, В, Г). В узле А соединены три ветви с токами I1, I4, I5, в узле Б соединены четыре ветви с токами I1, I2, I6, I7. 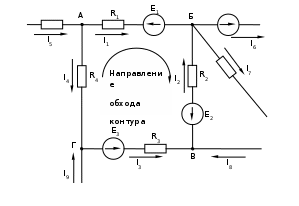 Рисунок 3.2 Часть схемы электрической цепи Иногда под узлом понимают шину (отрезок провода большого сечения), практически не обладающего сопротивлением, к которой присоединены не менее трех ветвей или проводов. Контур электрической цепи представляет собой замкнутый путь, проходящий по нескольким ветвям, например контур из 4-х ветвей на рисунке 3.2. При постоянных токах в цепи ни в одной из её точек не могут накапливаться электрические заряды, так как это вызвало бы изменение потенциалов точек цепи и напряжений на участках. Следовательно, электрические заряды, притекающие к какому-либо узлу по одной части присоединенных к нему ветвей в единицу времени, равны зарядам, оттекающим от этого узла по другой части ветвей за ту же единицу времени. Это положение выражает первый закон Кирхгофа, который формулируется так: сумма токов, направленных к узлу, равна сумме токов, направленных от узла. Пользуясь этим законом, например, для узлов А и Б на рисунке 2.2. можно написать:   или   В общем виде  т.е. алгебраическая сумма токов в узле равна нулю, причем со знаком плюс записываются втекающие токи, а со знаком минус вытекающие (или наоборот). Если направления токов в ветвях не известны, то при составлении уравнений по законам Кирхгофа их необходимо предварительно выбрать произвольно и обозначить на схеме стрелками. В действительности направления токов в ветвях могут и не совпадать с произвольно выбранными. Поэтому выбранные направления токов называют положительными направлениями. Если в результате расчета какие-либо токи будут выражены отрицательными числами, то действительные направления этих токов обратны выбранным положительным. Обходя контур АБВГА, рисунок 3.2, от точки А, имеющей потенциал , в произвольно выбранном направлении, например по часовой стрелке, проследим за изменением потенциала. На участке цепи АБ потенциал уменьшается на падение напряжения  , так как направление обхода совпадает с направлением тока, который на внешних участках цепи течет от точек с более высоким потенциалом к точкам с меньшим потенциалом. Кроме того, на этом же участке потенциал уменьшается на значение ЭДС Е1, так как при обходе контура идем на встречу ЭДС – переходим от положительного вывода источника питания к его отрицательному выводу. Таким образом,  При дальнейшем обходе контура от точки Б к точке В потенциал увеличивается на падение напряжения  , так как направление обхода противоположно направлению тока I2, который в резисторе R2 течет от точки с более высоким потенциалом к точке с более низким потенциалом. На этом же участке при переходе от отрицательного вывода источника ЭДС Е2 к его положительному выводу имеем повышение потенциала на значение ЭДС Е2. Поэтому:  Обойдя весь контур и вернувшись в исходную точку А, получим снова потенциал , т.е.  Перенеся все падения напряжения в правую часть уравнения, найдем, что  Или в общем виде  Это уравнение выражает второй закон Кирхгофа: в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжения на всех сопротивлениях. При составлении уравнений по второму закону Кирхгофа ЭДС записывается со знаком “+”, если её направление совпадает с направлением произвольно выбранного обхода контура. В противном случае ЭДС записывается со знаком “-”. Падение напряжения на сопротивлении записывается со знаком “+”, если направление тока в нем совпадает с направлением обхода. Метод узлового напряжения (двух узлов)Метод узлового напряжения дает возможность более просто, по сравнению с другими методами, определить режим цепи с двумя узлами. Поэтому этот метод расчета имеет и другое название – метод двух узлов. Действительные направления токов до расчета режима нельзя указать, так как они зависят от значений ЭДС и сопротивлений. Поэтому выберем положительные направления токов так, как показано стрелками на рисунке 2.3. 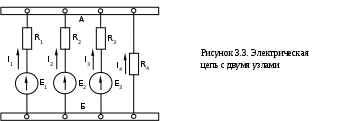 Определим разность потенциалов между двумя узлами А и Б, которая называется узловым напряжением  Перемещаясь по первой ветви от узла Б к узлу А, найдем потенциал точки А:  или    откуда ток первой ветви  здесь R1 и G1 – сопротивление и проводимость первой ветви, в которые входит и внутреннее сопротивление первого источника. Аналогично для остальных ветвей цепи:    По первому закону Кирхгофа для узла А:  Подставив в последнее уравнение выражения токов ветвей, получим:  Раскрыв скобки, найдем узловое напряжение:  или в общем случае узловое напряжение  Таким образом, узловое напряжение равно отношению алгебраической суммы произведений ЭДС на проводимости соответствующих ветвей к сумме проводимостей всех ветвей. Со знаком «+» записываются ЭДС, направленные к узлу А. Если какая-либо из ЭДС имеет противоположное направление, то она войдет со знаком «-». Найдя узловое напряжение и подставив его в выражение для токов, можно определить токи во всех ветвях цепи. 4. Произвести расчет приведенной в задаче 1.1 схемы согласно варианту. Вариант- положение второй ЭДС в одной из ветвей и ее величина, определяется как номер студента в журнале. Ввиду меньшего числа ветвей, чем число студентов в группе номер варианта по ветвям не превышает трех, потом повторяется. Вариант по величине ЭДС индивидуален для каждого студента. Провести проверку полученных расчетных результатов моделированием цепи в Электроникс Воркбенч. 3.Контрольные вопросыСформулируйте первый и второй законы Кирхгофа. Какое соединение электрической цепи считается смешанным? Поясните принцип расчета электрической цепи методом составления узловых и контурных уравнений Кирхгофа. Поясните принцип расчета электрической цепи методом двух узлов. |