Практическая работа. Практическая работа 4 циклический алгоритм while

• Название: Практическая работа 4 циклический алгоритм while
• Дата: 21.03.2021
• Размер: 217.38 Kb.
• Имя файла: Практическая работа.docx
• Тип: Практическая работа; #186725

Практическая работа №4

ЦИКЛИЧЕСКИЙ АЛГОРИТМ WHILE

Цель практической работы

Приобретение практических навыков разработки и программирования

вычислительного процесса с использованием оператора while.

Задачи для самостоятельного решения

Вводится последовательность вещественных чисел, не равных нулю. Известно, что для завершения последовательности нужно ввести 0. В программе должны вычисляться суммы всех положительных и всех отрицательных чисел. Разработайте алгоритм и программу.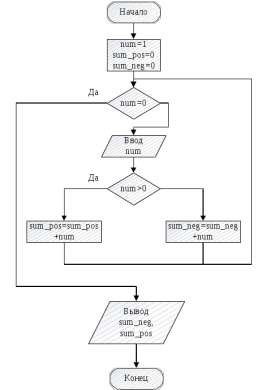


# -*- coding: cp1251 -*-

def isfloat(value):

try:

float(value)

return True

except ValueError:

return False
def isint(value):

try:

int(value)

return True

except ValueError:

return False
num=1.0

num_out=0.0

sum_pos=0.0

sum_neg=0.0

while (num != num_out):

s=input("Введите любое вещественное число или 0 для выхода ")

if isfloat(s) or isint(s):

num=float(s)

if num < 0:

sum_neg=sum_neg+num

else:

sum_pos=sum_pos+num
print("Сумма положительных элементов = {:.3f}".format(sum_pos)," Сумма отрицательных элементов = {:.3f}".format(sum_neg))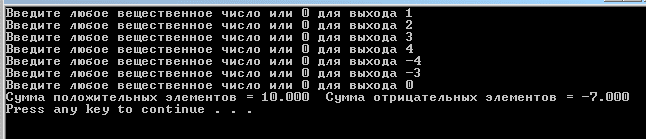


Вычислите сумму четных чисел на отрезке от 10 включительно до 30 включительно. Разработайте алгоритм и программу, используя цикл while.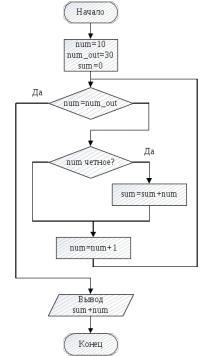


# -*- coding: cp1251 -*-
num=10

num_out=30

sum=0

while (num != num_out):

if num % 2 ==0:

sum=sum+num

num+=1

print("Сумма четных чисел от 10 до 30 = ", sum+num)

Задание на практическую работу

Вариант 18

Вычислите корень уравнения x- 0,5*(sin(x²)-1) = 0 с точностью  = 0,001, воспользовавшись итерационной формулой:

x_i+1 = 0,5*(sin(x_i²)-1), где i = 0,1,2…, x₀ = -0,25

Проверьте правильность решения подстановкой найденного корня в уравнение.
Алгоритм решения:

1. 
   Задаем начальное приближение х0=-0.25
   
2. 
   Вычисляем следующее приближение по формуле
   

x_i+1 = 0,5*(sin(x_i²)-1)

3. 
   Проверяем выполнение условия |x_i+1 - x_i| <  = 0.001
   

если условие не выполняется, то x_i = x_i+1 и идем на п.2

в противном случае выводим значение корня x_i+1 и f(x_i+1)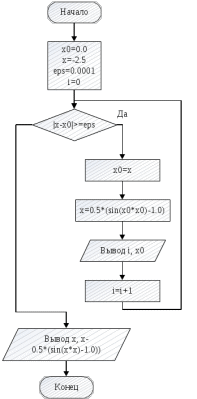


# -*- coding: cp1251 -*-

import math

# Вариант 18

# Выполнил

x0=-2.5

x=0.0

eps=0.0001

i=0
while math.fabs(x-x0)>=eps:

x0=x

x=0.5*(math.sin(x0*x0)-1.0)

print("i = ",i," x = {:.5f}".format(x))

i+=1
print("Левая часть уравнения при x= {:.5f}".format(x)," равна {:.5f}".format(x-0.5*(math.sin(x*x)-1.0)))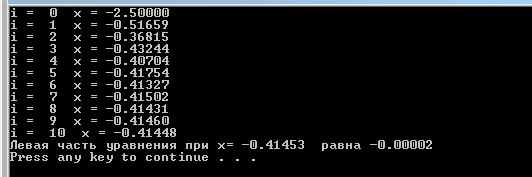

Выводы

В результате выполнения работы приобретены практические навыки разработки и программирования вычислительного процесса с использованием оператора while.

Контрольные вопросы для защиты лабораторной работы

1. 
   В каких случаях применяются циклы с неизвестным числом повторений.
   

При решении некоторых задач может возникнуть ситуация, когда невозможно заранее определить количество повторений вычислений. В таких случаях речь идет о циклах с неизвестным числом повторений.

В циклах с неизвестным числом повторений вычислительный процесс завершается при выполнении некоторого дополнительного условия. Значения параметра цикла уже не задаётся в виде диапазона, а только указывается его начальное значение и шаг изменения.

2. 
   
   Какая циклическая структура может считаться итеративной?
   

Циклическая структура, в которой число повторений цикла заранее неизвестно, а определяется только в процессе выполнения алгоритма, называется итеративной циклической структурой. 

3. 
   Нарисуйте общий вид алгоритма оператора цикла while.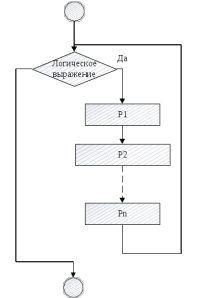
   

4. 
   Напишите синтаксис оператора цикла while.
   

while test_expression:

body of while

5. 
   Опишите работу оператора цикла while. Приведите примеры.
   

Сначала программа оценивает условие цикла while. Если оно истинное, начинается цикл, и тело while исполняется. Тело будет исполняться до тех пор, пока условие остается истинным. Если оно становится ложным, программа выходит из цикла и прекращает исполнение тела.

a = 1

while a < 10:

print('Цикл выполнился', a, 'раз')

a = a+1

print('Цикл окончен')

Вывод:

Цикл выполнился 1 раз

Цикл выполнился 2 раз

Цикл выполнился 3 раз

Цикл выполнился 4 раз

Цикл выполнился 5 раз

Цикл выполнился 6 раз

Цикл выполнился 7 раз

Цикл выполнился 8 раз

Цикл выполнился 9 раз

Цикл окончен

6. 
   
   В каких случаях применяются рекуррентные соотношения?
   

Будем говорить, что последовательность векторов 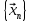 задана рекуррентным соотношением, если задан начальный вектор 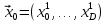 и функциональная зависимость последующего вектора от предыдущего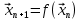



Вектора 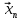  можно интерпретировать как наборы значений переменных. Таким образом, они характеризуют состояние вычислительного процесса. Функцию   будем понимать как преобразование значений переменных на каждом шаге цикла.

7. 
   Расскажите об алгоритме вывода рекуррентной формулы.
   

Рассмотрим на примере.

Известно разложение в ряд: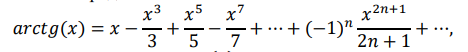



Найдем отношение последующего члена последовательности а_к к предыдущему а_k-1: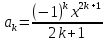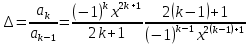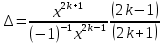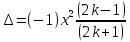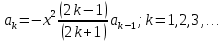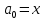












т.е., если известен общий член ряда, то рекуррентное соотношение определяется из соотношения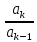