Практическая работа. решение вариант 6. Практическая работа Электромеханические системы автоматики
 Скачать 107.49 Kb. Скачать 107.49 Kb.
|
|
Федеральное агентство по образованию Уральский государственный лесотехнический университет Кафедра автоматизации производственных процессов Практическая работа «Электромеханические системы автоматики» Руководитель доц. к.т.н. Тойбич В. Я. «___» ___________ 2021 г. Работу выполнил студент группы АПП-41З Возжаев Д. С. «___» ___________ 2021 г. Екатеринбург 2021г. Практическое задание №7 Расчет мощности и выбор электродвигателя для системы автоматики по заданным условиям эксплуатации, нагрузочной диаграмме и тахограмме Исходные данные (вариант 6) Рассчитать мощность и выбрать электродвигатель для системы автоматики по следующим исходным данным: 1. Скорость вращения вала механизма нагрузки nм = 100 об/мин; 2. Момент инерции механизма нагрузки Jм = 0,02 кг·м2; 3. Примерное значение КПД редуктора, соединяющего “тихоходный” вал нагрузки с “быстроходным” валом двигателя ɳp = 0,91 о.е.; 4. Ориентировочное значение тепловой постоянной двигателя Tm = 15 мин; 5. Условия эксплуатации: система автоматизации стационарной установки с повторяющейся диаграммой нагрузки (рис. 1). 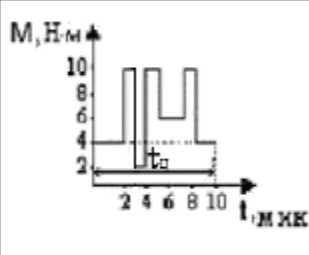 Рисунок 1 – Диаграмма нагрузки двигателя Необходимо: 1. Рассчитать мощность и выбрать тип двигателя; 2. Определить передаточное отношение и число ступеней сцеплений редуктора, а также его КПД; 3. Выполнить разбивку передаточного отношения редуктора по ступеням сцеплений “шестерня-колесо”; 4. Определить оптимальное значение передаточного отношения редуктора, обеспечивающего максимальное ускорение вращения вала нагрузки; 5. Вычислить максимальное ускорение вала двигателя и определить минимальное время пуска; 6. Определить время пуска двигателя на холостом ходу и под нагрузкой (для фактического значения передаточного отношения редуктора); 7. Начертить функциональную схему включения двигателя, обеспечивающую его пуск и плавное регулирование скорости вращения. Решение 1. В соответствии с повторяющимся характером диаграммы нагрузки, а также величиной тепловой постоянной ТН двигатель надо выбирать как работающий в длительном режиме работы с переменной нагрузкой. В этом случае расчетную мощность двигателя определяем по формуле: 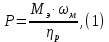 где MЭ – эквивалентное по нагреву значение момента нагрузки; ωм – номинальная угловая скорость механизма нагрузки. 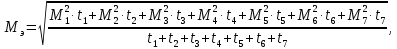 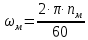 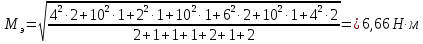 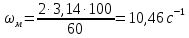 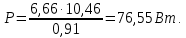 По каталогу находим двигатель, удовлетворяющий условиям эксплуатации, с номинальной мощностью РН>P. Выбираем двигатель постоянного тока параллельного возбуждения типа СЛ – 569 со следующими номинальными значениями параметров: - номинальное напряжение якоря Uн =110 В; - номинальная мощность Pн = 175 Вт; - номинальный ток якоря Iян = 2,2 А; - номинальная частота вращения nд = 3600 об/мин; - номинальный момент двигателя Мдв=0,425 Н·м; - пусковой момент двигателя Мп = 1,05 Н·м; - сопротивление обмотки якоря Rя = 3,6 Ом; - сопротивление обмотки возбуждения Rов = 880 Ом; - коэффициент самоиндукции якоря Lя = 30 мГн; - момент инерции якоря двигателя Jд = 2,5·10-4 кг·м2; - масса двигателя m = 4,5 кг ; - габаритные размеры D×L = 108 мм×173 мм. Передаточное отношение понижающего редуктора должно составлять: 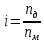 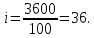 Проверим выполнение необходимых условий работы двигателя 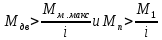 Указанные условия выполняются, т.к. 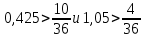 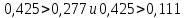 2. В системах автоматики малой мощности, особенно в следящих системах (СС) с двухфазным асинхронным двигателем с полым ротором, большое значение имеет распределение общего передаточного отношения редуктора i между отдельными парами зубчатых колес из условия обеспечения наименьшего приведенного к валу двигателя момента инерции нагрузки. Недопустимо, чтобы момент инерции нескольких первых колес (шестерен) оказался соизмеримым или в несколько раз большим момента инерции ротора двигателя Jд. При одинаковых видах кинематических передач во всех ступенях редуктора для уменьшения ошибки “мертвого хода”, который может вызвать автоколебания в СС, необходимо выполнить условие: 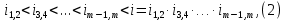 где 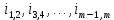 - передаточные отношения соответственно первой, второй и т.д. пар “шестерня-колесо”. - передаточные отношения соответственно первой, второй и т.д. пар “шестерня-колесо”.Для получения минимальных габаритов редуктора близкое к оптимальному число опт m пар “шестерня-колесо” редуктора можно определить: 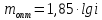 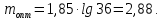 Округлим число ступеней редуктора 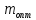 до целого числа 3. до целого числа 3.Кинематическая схема электропривода с трехступенчатым понижающим редуктором показана на рис. 1. На рис. 2. приведены номограммы для определения передаточных отношений отдельных пар “шестерня-колесо” при заданном общем передаточном отношении редуктора. Кривые 1, 2, 3 и 4 соответствуют редукторам соответственно с двумя, тремя, четырьмя и пятью парами сцеплений “шестерня-колесо”, причем все шестерни редуктора имеют одинаковые диаметры и массу. Из кривой 2 рис.2. для i = 36 определим передаточное отношение i1,2 первой пары “шестерня-колесо”, i1,2=2,14. 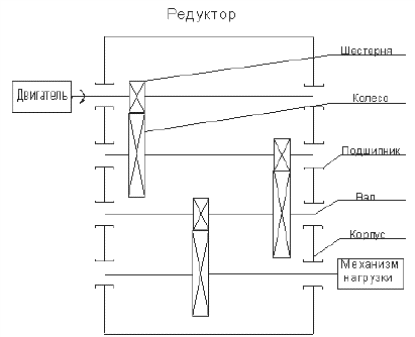 Рисунок 1 – Кинематическая схема электропривода 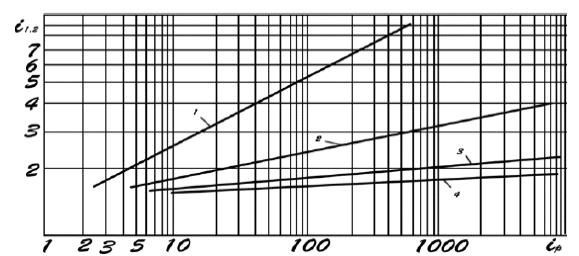 Рисунок 2 – Номограммы для определения передаточных отношений пар шестерня-колесо редуктора Тогда общее передаточное отношение второй и третьей пар сцеплений редуктора: 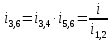 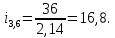 Из кривой 1 рис.2. для i = 16,8 определим 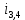 =3,06 , считая мысленно пару 3,4 первой в двухступенчатом редукторе. Тогда =3,06 , считая мысленно пару 3,4 первой в двухступенчатом редукторе. Тогда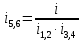 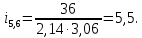 Рекомендуемое неравенство (2) выполняется, т.к. 2,14 < 3,06 < 5,5. Уточним КПД редуктора по кинематической схеме рис.1, считая что все три зубчатые передачи в редукторе выполнены прямозубыми цилиндрическими шестернями и колесами, а все четыре его вала опираются на подшипники качения. 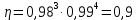 Так как уточненное значение КПД редуктора отличается от принятого ранее ориентировочного значения менее чем на 3%, то вычислять новое значение расчетной мощности двигателя по формуле (1) не требуется. 3. Определим оптимальное передаточное отношение редуктора iопт, обеспечивающее максимальное ускорение вала нагрузки и, следовательно, максимальное быстродействие системы управления 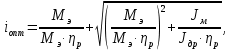 где 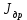 - момент инерции двигателя и редуктора, - момент инерции двигателя и редуктора, 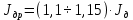 . .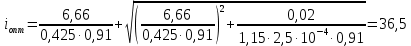 Так как iопт отличается от ранее полученного передаточного отношения i редуктора на 2 %, то возвращаться к выбору нового двигателя из каталога не следует. 4. Определим максимальное угловое ускорение вала двигателя ɛдв.макс и соответствующее ему ориентировочное значение времени пуска 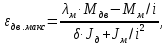 где 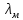 - допустимый коэффициент перегрузки двигателя по моменту. Принимаем - допустимый коэффициент перегрузки двигателя по моменту. Принимаем 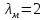 , поскольку из физических соображений , поскольку из физических соображений 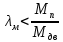 , т.е. , т.е. 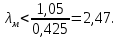 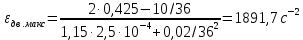 или в других единицах изменения 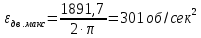 Если бы разгон двигателя до номинальной частоты вращения nн происходил равноускорено с ускорением 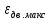 , то время пуска tП двигателя составило , то время пуска tП двигателя составило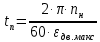 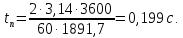 5. Определим время пуска двигателя под нагрузкой и на холостом ходу. При подключённой нагрузке: 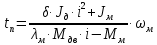 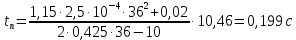 На холостом ходу полагаем ММ = 0, JM = 0. В этом случае 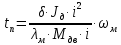 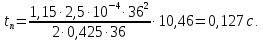 6. На рис.3. представлена функциональная схема, обеспечивающая плавное регулирование скорости вращения двигателя. Такая схема обеспечит поддержание неизменной угловой скорости вала двигателя при изменениях момента механизма нагрузки в соответствии с диаграммой нагрузки. Датчиком угловой скорости вала двигателя выбираем тахогенератор постоянного тока типа СЛ-221 с максимальной частотой вращения 3700 об/мин, удельной ЭДС 1,5 В/(об/с) и сопротивлением обмотки якоря RЯTГ = 117 Ом. Делитель напряжения ДН, как правило, выполняют Г-образным на двух резисторах, номинальные значения сопротивлений, которых и их допустимые мощности рассеяния легко рассчитать, полагая входное сопротивление нормирующего усилителя НУ, близким к бесконечности. 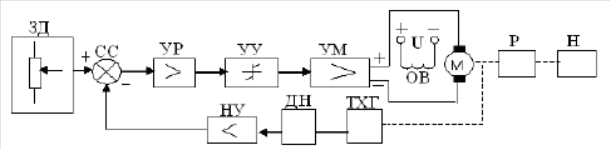 Рисунок 3 – Функциональная схема управления двигателем постоянного тока На функциональной схеме использованы следующие обозначения: ЗД – задающее устройство; СС – схема сравнения; УР – усилитель рассогласования; УУ – управляющее устройство; УМ – усилитель мощности; М – двигатель (мотор); ОВ – обмотка возбуждения двигателя постоянного тока независимого возбуждения; Н – механизм нагрузки; ТХГ – тахогенератор постоянного тока; ДН – делитель напряжения; НУ – нормирующий усилитель; Р – редуктор. |
