Лб 3. Практическая работа метод анализа и коррекции детерминированной модели процесса

• Название: Практическая работа метод анализа и коррекции детерминированной модели процесса
• Дата: 05.11.2021
• Размер: 105.74 Kb.
• Имя файла: Лб 3.docx
• Тип: Практическая работа; #263698

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Сибирский государственный университет науки и технологий

имени академика М.Ф. Решетнева»
Институт информатики и телекоммуникаций

Кафедра автоматизация производственных процессов
Практическая работа
МЕТОД АНАЛИЗА И КОРРЕКЦИИ ДЕТЕРМИНИРОВАННОЙ МОДЕЛИ ПРОЦЕССА
Вариант 5

Исполнитель:
Студент группы МХТ20-01
Копылова Екатерина Владимировна

_____________

(подпись)

________________________

(дата)

Руководитель:
_____________ Лосев В.В.

(подпись)

________________________

(оценка, дата)

Красноярск

2020

Исходные данные:
1 Число взаимосвязанных вершин графа – не менее 13 пар

2 Число нарушений регламента – не менее 5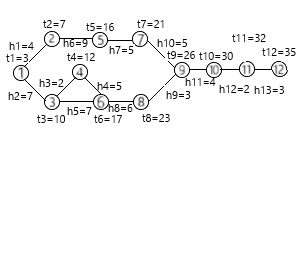



Рисунок 1 – Исходный граф

1. Запись ВВР и ВР в соответствии с заданием

ВВР:

{t_i} = {t₁=3±1; t₂=7±3; t₃=10±2; t₄=12±2; t₅=16±3; t₆=17±3; t₇=21±2; t₈=23±2; t₉=26±2; t₁₀=30±1; t₁₁=32±1; t₁₂=35±1}.

Значения компонент вектора ВВР соответствуют моменту начала исполнения операции. Для каждого компонента ВВР зададим временной параметр.

ВР:

{h_j} = {h₁=4; h₂=7; h₃=2; h₄=5; h₅=7; h₆=9; h₇=5; h₈=6; h₉=3; h₁₀=5; h₁₁=4; h₁₂=2; h₁₃=3}.

Значения компонент вектора реализации определяют длительность исполнения операции, находящейся в начале j-й дуги.

2. Анализ и коррекция ВВР

Основное условие, которое должно выполняться при анализе ВВР, представлено в виде неравенства: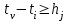
. (1)
Если данное условие не выполняется, то ВВР нереализуем. В этом случае необходимо провести коррекцию в рамках существующих интервалов. Замена значений ВВР производится по правилу: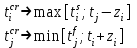
, (2)
где z_i – длительность реализации операции, которая находится в t_i вершине.
1) t₂ – t₁ ≥ h₁ условие выполняется t₂ =7;

7 – 3 ≥ 4;
2) t₃ – t₁ ≥ h₂ условие условие выполняется t₃ = 10

10 – 3 ≥ 7
3) t₄ – t₃ ≥ h₃ условие не выполняется проведем коррекцию:

12 – 10 ≥ 4

t₄^cr= min (12+2; 10+4) = 14 t₄^cr =14

14 – 10 ≥ 4 условие выполняется
4) t₆ – t₄^cr ≥ h₄ условие не выполняется проведем коррекцию:

17 – 14 ≥ 3

t₆^cr= min (17+3; 14+6) = 20 t₆^cr =20

20 – 14 ≥ 6 условие выполняется
5) t₆^сr – t₃ ≥ h₅ условие условие выполняется t₆^cr =20;

20 – 10 ≥ 10
6) t₅ – t₂ ≥ h₆ условие выполняется t₅ =16;

16 – 7 ≥ 9
7) t₇ – t₅ ≥ h₇ условие выполняется t₇ =21;

21 – 16 ≥ 5
8) t₉ – t₈ ≥ h₉ условие не выполняется проведем коррекцию:

26 – 23 ≥ 4

t₉^cr= min (26+1; 23+4) = 27 t₉^cr =27

27 – 23≥ 4 условие выполняется
9) t₉^cr – t₇ ≥ h₁₀ условие выполняется t₉^сr =27;

27 – 21 ≥ 6
10) t₈ - t₆^cr ≥ h₈ условие выполняется t₈ =23;

23 – 20 ≥ 3
11) t₁₀ – t₉^cr ≥ h₁₁ условие не выполняется проведем коррекцию:

30 – 27 ≥ 4

t₁₀^cr= min (30+1; 27+4) = 31 t₁₀^cr =31

31 – 27 ≥ 4 условие выполняется
12) t₁₁ – t₁₀^cr ≥ h₁₂ условие не выполняется проведем коррекцию:

32 – 31 ≥ 3

t₁₁^cr= min (32+2; 31+3) = 34 t₁₁^cr =34

34 – 31 ≥ 3 условие выполняется
13) t₁₂^cr – t₁₁^cr ≥ h₁₃ условие не выполняется проведем коррекцию:

35 – 34 ≥ 3

t₁₂^cr= min (35+2; 34+3) = 37 t₁₂^cr =37

37 – 34 ≥ 3 условие выполняется
Из полученных результатов запишем скорректированный ВВР:

ВВР:

{t_i} = {t₁=3; t₂=7; t₃=10; t₄=14; t₅=16; t₆=20; t₇=21; t₈=23; t₉=27; t₁₀=31; t₁₁=34; t₁₂=37}.
Изобразим результирующий граф с учетом скорректированных вершин


t₇=21

t₅=16

t₂=7


h₁₀=6

h₇=5

h₆=9

h₁=4

5

22

7



t₁₂=37

t₁₁=34

t₁₀=31


h₁₁=4

t₉=27

t₄=14

t₁=3

111

100000000

9

12

1

4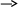

h₁₃=3

h₁₂=3

h₉=4

h₈=3

h₅=10

h₄=6

h₃=4

h₂=7

t₈=23

t₆=20

t₃=10

3

6

8


Рисунок 2 – Результирующий граф
Определим длительность всего процесса:
T = max (t_i) – min (t_i) = 37 – 3 = 34 у.е.в.,

где у.е.в. - условная единица времени;
Вывод: после проведения анализа и коррекции значений вектора ВВР в соответствие с вектором реализации, ВВР стал реализуем, но длительность выполнения всего процесса увеличилась на 2 у.е.в.