ПРАКТИЧЕСКАЯ РАБОТА ПО ДИСЦИПЛИНЕ «Методы анализа данных». Практическая работа по дисциплине модели и методы предиктивной аналитики
 Скачать 0.57 Mb.
|
Институт информационных технологий КАФЕДРА ПРАКТИЧЕСКОЙ ПРИКЛАДНОЙ ИНФОРМАТИКИ (ППИ) ПРАКТИЧЕСКАЯ РАБОТА ПО ДИСЦИПЛИНЕ «МОДЕЛИ И МЕТОДЫ ПРЕДИКТИВНОЙ АНАЛИТИКИ» Выполнил студент группы Принял профессор кафедры ПМ Кузьмин В.И. Практическая работа выполнена «___»_______2023 г. «Зачтено» «___»_______2023 г. Москва 2023 ВВЕДЕНИЕ Судоходство начало свое развитие с давних времен. В современном мире ежегодно более 80% всего объема мировой торговли осуществляется по морю. Так же имеются изменения и в пассажирских перевозках. Статистические показатели в данной сфере показывают ежегодный рост: в 2012 году пассажирооборот морского транспорта в России составил 52 млн. пассажиро-км, хотя в 2000 году он составлял 22 млн. Такая динамика развития возможна благодаря усовершенствованию судопроизводства. В данной работе произведен анализ различных судов и их основных характеристик. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Данные для анализа были получены из интернета, откуда была взята информация о 239 гражданских судов с различными характеристиками, выпущенными в производство в период от 1952 по 2003 год. Для оценки были использованы следующие характеристики: Крейсерская скорость (км/ч); Дальность плавания (км); Высота (км); Грузоподъемность (кг); Масса пустого судна (кг); Вех(ширина) (м); Lex(длина) (м); В (ширина) (м); Осадка (м); Тяга (Н); Дата выпуска. Ранее мы работали только с одномерными рядами данных, находили закономерности их динамики. Но на самом деле, чаще всего приходится исследовать системы, характеризующиеся большим количеством параметров. Одним из способов анализа разноразмерных характеристик является построение безразмерных комплексов. Из имеющегося набора характеристик были построены четыре безразмерных комплекса.
Также в вычислениях использовались физические константы.
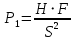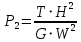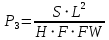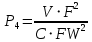    Еще одним методом является масштабирование относительно системы естественных критических единиц. Такими значениями является система реперов, предложенная Руарком:
Рассчитаем реперное значение для Силы (кг*м/с2), подставляя значение кг, м и с из таблицы выше получим величину для силы, равную 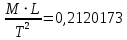 . Теперь, имея отмасштабированные характеристики, можно рассматривать их динамики, ранговые распределения и соотношения друг с другом.В работе применяются следующие методы анализа полученных показателей: Графические представления; Ранговые распределения; Диаграммы рассеивания. ХОД РАБОТЫ Для каждого комплекса было построено ранговое распределение, и график в полулогарифмическом масштабе. 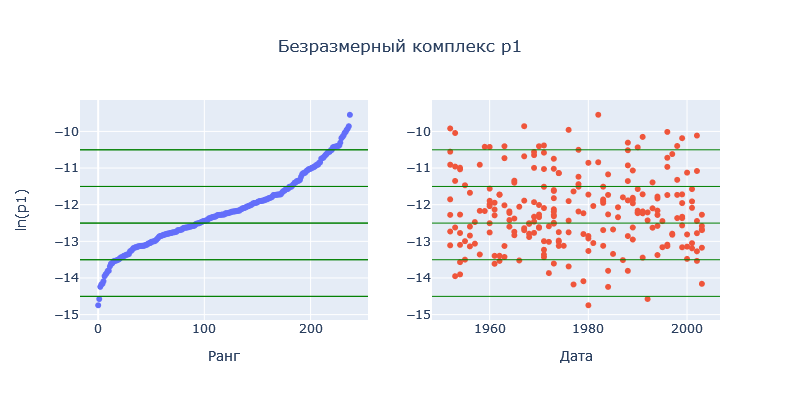 Рисунок 1 — Первый безразмерный комплекс 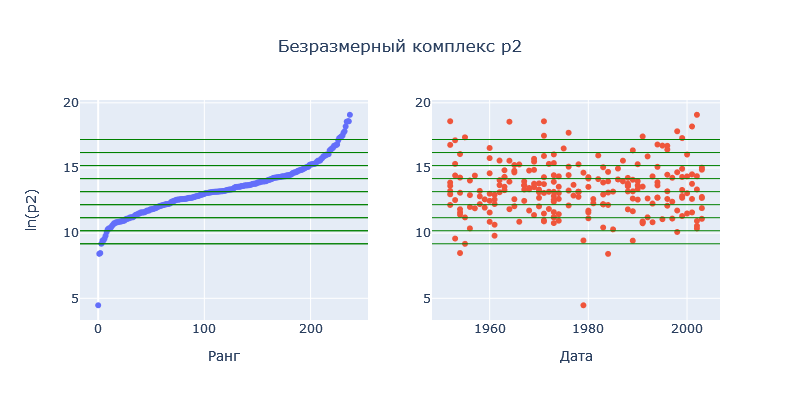 Рисунок 2 — Второй безразмерный комплекс 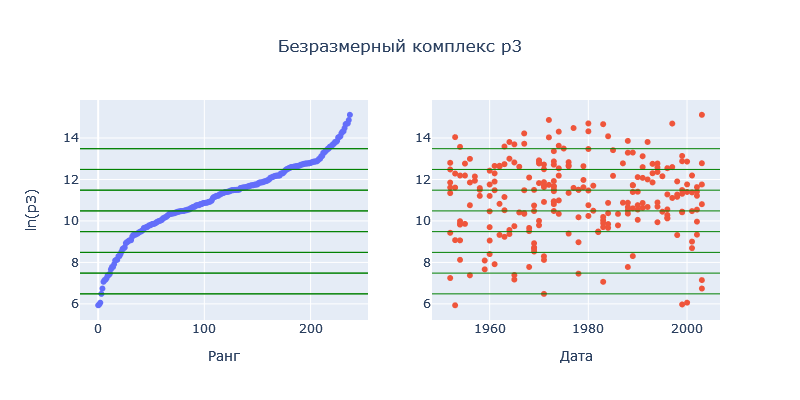 Рисунок 3 — Третий безразмерный комплекс Рисунок 4 — Четвертый безразмерный комплекс На графиках безразмерных комплексов четко прослеживаются уровни квантования по экспоненте. Построим графики зависимостей безразмерных комплексов друг от друга. 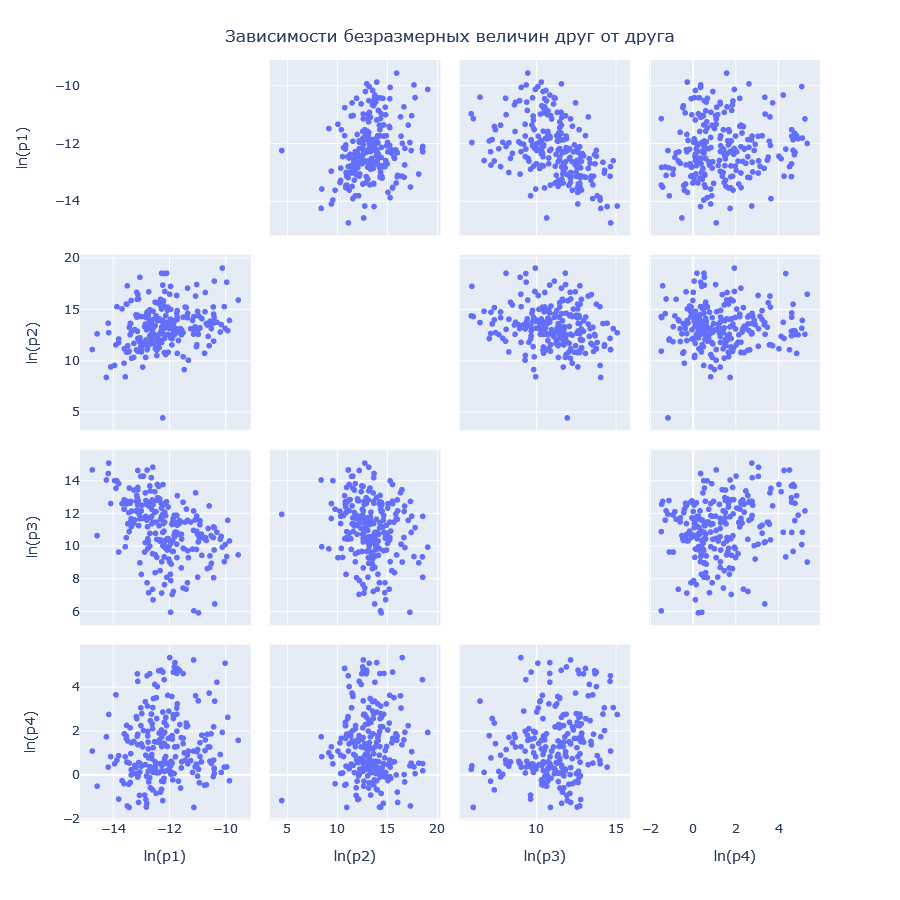 Рис. 2. Зависимости безразмерных величин друг от друга Рассмотрим график в координатах 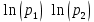 . 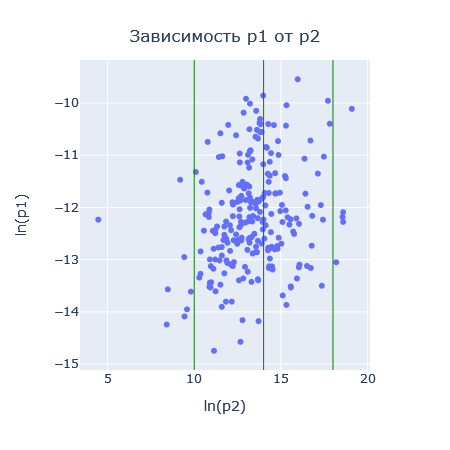Рисунок 3 – Зависимость p1 от p2 На графике в координатах 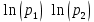четко прослеживается квантование по экспоненте. В левом нижнем углу находятся дальнемагистральные суда, по середине графика – среднемагистральные, а в правом верхнем углу – ближнемагистральные. Квантование поделило суда по семействам:В промежутке от 5 до 10 расположились большие корабли для грузоперевозок, танкеры и криузные лайнеры; В промежутке от 10 до 14 расположились средне- и дальнемагистральные суда как для пассажирских, так и для грузовых перевозок; В промежутке от 14 до 18 расположились ближнемагистральные суда, преимущественно для пассажирских перевозок; В промежутке от 18 до 20 расположились суда в основном для коротких перевозок в реках. Рассмотрим график в координатах 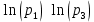 .    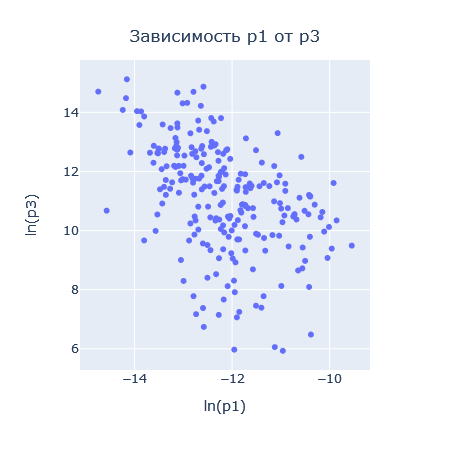Рисунок 7 — Зависимость p3 от p1 На графике можно заметить тренд определяющийся прямой, линию поддержки и линию сопротивления. Рассмотрим соотношение тяги и взлетного веса. Для нормирования поделим исходные характеристики на соответствующие им реперные значение и вычислим логарифм от полученных значений. 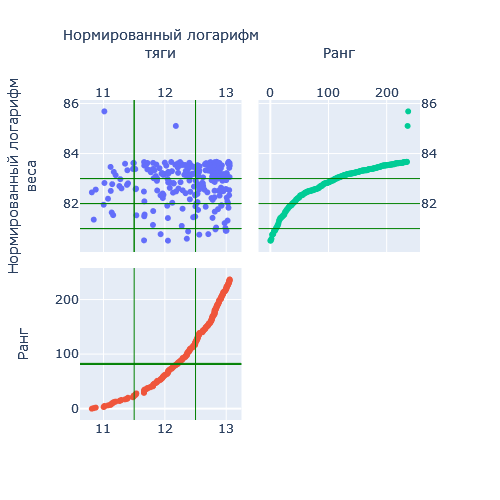 Рисунок 8 — Зависимость между весом и тягой В левом нижнем углу расположились суда с низкими показателями грузоподъёмного веса и тяги, подходящими для судов ближне- и среднемагистрального типов. В правом верхнем углу графика расположились дальнемагистральные суды. Рассмотрим график зависимости логарифмированных показателей дальности плавания и скорости. На графике можно увидеть уменьшение разброса значений скорости при увеличении дальности плавания. 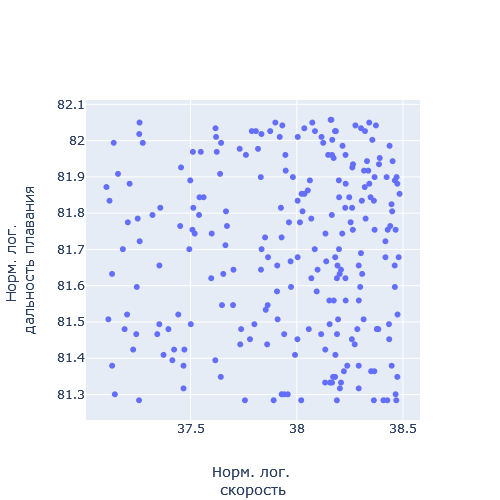 Рисунок 9 — Логарифмическая зависимость дальности плавания от скорости судна Можно заметить, что уменьшение начинает происходит на уровне 38. Рассмотрим нормированную логарифмированную зависимость показателей подъемности и дальности плавания. 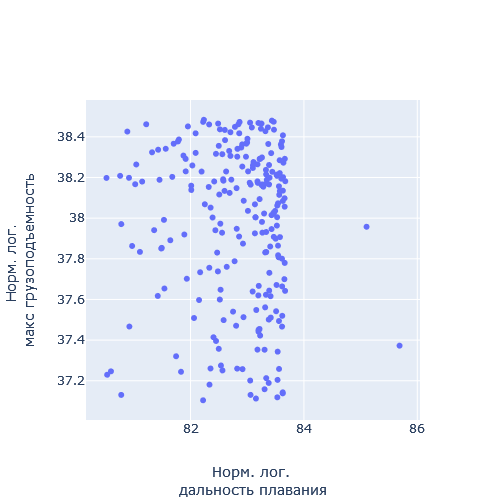 Рисунок 10 — Зависимость нормированных логарифмированных показателей грузоподъемности и дальности плавания На графике видно, что при увеличении дальности плавания, увеличивается и макс. грузоподъемность, причем дальность плавания сильно ограничена на уровне 83. ЗАКЛЮЧЕНИЕ В ходе данной работы были проанализированы данные о более чем 230 судов. Мы смогли сделать кластеризацию судов по их типам: ближне-, средне- и дальнемагистральные, выделили и определили оптимальные уровни дальности плавания и грузоподъемности. СПИСОК ЛИТЕРАТУРЫ Модели и методы научно-технического прогнозирования: учебное пособие / В.И. Кузьмин, А.Ф. Гадзаов. – М.: МИРЭА, 2016. – 90 с. |
