Задания. Практическое занятие №2. Практические занятия 2

• Название: Практические занятия 2
• Анкор: Задания
• Дата: 05.12.2022
• Размер: 50 Kb.
• Имя файла: Практическое занятие №2.doc
• Тип: Закон; #829838

Практические занятия №2

«Определение показателей надёжности при различных законах функционирования изделий (плотности вероятности отказов). Расчёт показателей надёжности нерезервированных систем»
1. Время безотказной работы гироскопического устройства с шарикоподшипниками в осях ротора гироскопа подчиняется закону Вейбулла с парамет­рами =1,5, =10^-4 1/час,а время его работы t=1800 часов. Требуется вычислить количественные характеристики надёжности такого устройства. Построить графики зависимостей Р(t), f(t) и (t).
2. Интенсивностьотказаэлектромеханическогоустройствазависитотвре­менииопределяетсяследующейформулой:

(t)=0,16∙10^-3∙t [1/час]

Определить зависимости P(t) и f(t), построить их графики, рассчитать T_ср.

Рассчитать вероятность безотказной работы изделия в течение 100 часов.
3. Плотность вероятности отказов изделия подчиняется закону Рэлея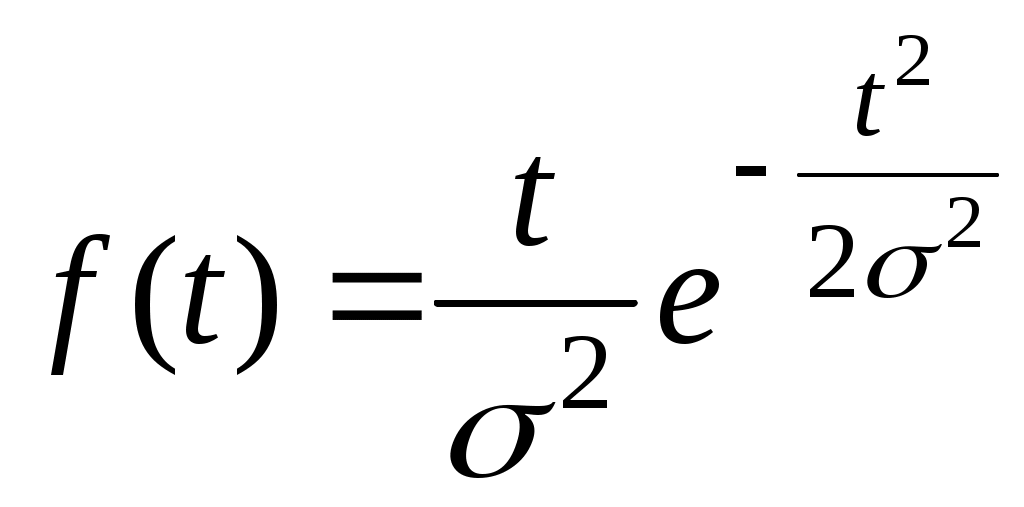



где =200 чaс.

Необходимо найти вероятность безотказной работы в течение 100 час Р(100), частоту отказов f(100) при t=100 часи среднюю наработку до первого отказа T_ср. Построить графики зависимостей P(t), f(t) и (t).
4. Какова вероятность безотказной работы объекта в течение средней на­работки до отказа, если аналитическое выражение интенсивности отказов имеет вид



Построить график зависимости P(t) для a=1, 2 и 3 1/час².
5. Какова вероятность безотказной работы объекта в течение средней на­работки до отказа, если плотность распределения наработки до отказа имеет вид



Вычислить математическое ожидание и дисперсию наработки до отказа для данного закона.
6.Плотность распределения наработки до отказа системы контроля имеет вид



Необходимо получить аналитические выра­жения для всех количественных показателей надежности, а именно, P(t), (t), T_ср. Построить графики P(t) и (t).
7. Плотность вероятности отказов изделия



где =0,62∙10^-3 l/чaс.

Необходимо найти вероятность безотказной работы в течение 100 час Р(100), частоту отказов f(100) при t=100 часи среднюю наработку до первого отказа T_ср. Построить графики зависимостей P(t), f(t) и (t).
8. Интенсивность отказов объекта управления зависит от времени и вы­ражается функцией



Требуется определить показатели надежности P(t), T_ср, f(t). Построить графики P(t) и f(t) для значений k=1, 2 и 3.
9. Определить, какова должна быть средняя наработка до отказа объекта, имеющего экспоненциальное распределение наработки до отказа, чтобы веро­ятность безотказной работы была не менее 0,99 в течение наработки t=300 ч. Построить график зависимости T_ср() для такого распределения.
10. Время безотказной работы блока аппаратуры подчинено усеченному нормальному закону с параметрами т=8000 ч, =1000 ч, 2000 ч, 3000 ч, 4000 ч. Определить вероят­ность безотказной работы блока для значений наработки 4000, 6000, 8000, 10000 ч. Вычислить Т_ср и построить графики зависимостей Р(t) для каждого значения . Сделать вывод о том, как влияет величина  на изменение Р(t) для времён меньших и больших, чем т.
11. Время исправной работы изделия подчинено закону Вейбулла с параметрами =2,6; t_с=0,6∙10³ час. Необходимо найти вероятность безот­казной работы, плотность вероятности отказов f(t) и интенсивность отказов изделия за время t=150 ч. Вычислить среднюю наработку до первого отказа. Построить графики зависимостей P(t) и (t).
12. Время исправной работы элемента системы подчинено распределению Вейбулла с параметрами =2,6; t_с=0,6∙10⁴ часов. Необходимо определить вероятность безотказной работы, плотность вероятности отказов f(t), интенсивность отказов элемен­та за 10000 ч, 5000 ч. Вычислить среднюю наработку до первого отказа изделия. Построить графики зависимостей P(t) и (t).
13. Система состоит из 5 приборов, причем отказ любого одного из них ведет к отказу системы. Известно, что первый прибор отказал 34 раза в течение 952 час. работы, второй — 24 раза в течение 960 час. ра­боты, а остальные приборы в течение 210 час. работы отказали 4, 6 и 5 раз соответственно. Требуется опреде­лить среднюю наработку до отказа системы в целом, если справед­лив экспоненциальный закон распределения плотности вероятности отказов для каждого из пяти приборов. Построить графики зависимостей Р(t) и (t).
14. Система состоит из трех блоков, средняя наработка до первого отказа которых равна Т₁=320 ч, Т₂=160 ч, Т₃=600 ч. Для блоков справедлив экспо­ненциальный закон надежности. Требуется определить среднюю наработку до первого отказа системы, построить график зависимости P(t).
15. Система состоит из двух устройств. Вероятности безотказной работы каждого из устройств в течение 100 ч равны P₁=0,95; Р₂=0,97. Справедлив экс­поненциальный закон надежности. Необходимо найти среднюю наработку до первого отказа системы и построить график зависимости P(t).
16. Вероятность безотказной работы одного элемента в течение времени t равна P(t)=0,9997. Требуется определить вероятность безотказной работы сис­темы, состоящей из 100 таких же элементов для данного времени.
17. Вероятность безотказной работы системы в течение времени tравна 0,95. Система состоит из 120 равнонадёжных элементов. Необходимо найти ве­роятность безотказной работы элемента.
18. При проектировании системы предполагается, что сложность ее не дол­жна превышать N_c=2500 элементов. Необходимо при обсуждении проекта тех­нического задания определить, может ли быть спроектирована система, к кото­рой предъявлено требование Т_ср=120 ч.
19. В системе 2500 элементов и вероятность безотказной работы ее в тече­ние 1 ч составляет 98%. Предполагается, что все элементы равнонадёжные. Тре­буется вычислить среднюю наработку до первого отказа системы и интенсив­ность отказов элементов.
20. Система состоит из пяти приборов, вероятности исправной работы ко­торых в течение 100 ч равны P₁=0,9996; P₂=0,9998; P₃=0,9996; P₄= 0,999; P₅=0,9998. Требуется определить плотность распределения наработки до отказа системы в момент времени t=100 ч.
21. Построить зависимость между наибольшим числом элементов N системы и интенсивностью отказов каждого элемента , если требуется обеспечить величину средней наработки системы до отказа T_ср=1000 ч при экспоненциальном законе распределения плотности вероятности отказов.