ПРАКТИЧЕСКОЕ ЗАДАНИЕ К РАЗДЕЛУ 1 (Экономика). Практическое задание к разделу 1 Форма практического задания
 Скачать 120.03 Kb. Скачать 120.03 Kb.
|
|
ПРАКТИЧЕСКОЕ ЗАДАНИЕ К РАЗДЕЛУ 1 Форма практического задания: расчетное практическое задание Примерные расчетно-практические задания к разделу 1: Задача № 1.1. Расчёт цены выбора Петров хочет купить мебельный гарнитур. Он должен затратить на поиски дешевого и качественного варианта 7 рабочих дней, для чего намерен взять отпуск без сохранения заработка. Если он не сделает этого, то купит гарнитур на 20% дороже. В день Петров зарабатывает 1000 руб. Какова должна быть цена гарнитура для того, чтобы рационально мыслящему Петрову было все равно – искать дешевый вариант или нет? Пусть х – цена гарнитура в рублях. 0,2 * х – величина переплаты, в случае если Петров не возьмёт отпуск. Если Петров возьмёт отпуск, то потери дохода составят: 7 * 1000 = 7000 р. Рационально мыслящему Петрову будет все равно – искать дешевый вариант или нет, если величина переплаты будет равна величине потерь дохода. Составим и решим уравнение: 0,2 * х = 7000 х = 35 000. Цена гарнитура должна быть равна 35 000 рублей. Задача № 1.2. Выбор более дешёвого способа передвижения Самолетом из Москвы во Владивосток можно добраться за 8 ч, но с учетом сопутствующих затрат времени можно считать, что сутки для работы или отдыха теряются. Поездка в поезде займет 9 дней. Авиабилет стоит 900 р., а железнодорожный билет 500 р. а) Какой способ передвижения дешевле для человека, зарабатывающего 50 р. каждый рабочий день с понедельника по пятницу. б) Если 4 из 9 дней пути на поезде приходятся на выходные, то сколько должен зарабатывать в будний день наш путешественник, чтобы ему было все равно с чисто экономической позиции - лететь в выходной день или ехать поездом? а) Для решения данной задачи и подобных задач удобно пользоваться таблицей, в которой сравниваются альтернативные затраты двух способов путешествия.
В расчёт недополученного заработка при поездке на поезде берём максимальное из 9 число будних дней, которое может истратить на поездку наш путешественник. Их будет 7. Значит, наибольшие потери дохода за 7 дней составят: 7 × 50 = 350 р. Следовательно, дешевле ехать поездом. б) Человеку будет безразлично с чисто экономической позиции - лететь в выходной день или ехать поездом, если альтернативная стоимость полёта на самолёте будет равна альтернативной стоимости поездки на поезде. Значит, ему должно быть всё равно либо вылететь в субботу, либо выехать в этот день поездом. Пусть W – дневной заработок в рублях в будний день. В случае полёта на самолёте он затратит 900 р. Потерь дохода в субботу нет. При путешествии на поезде затраты составят: 5 * W + 500. Составим и решим уравнение: 5 * W + 500 = 900 W = 80. Дневной заработок должен быть равен 80 р., тогда человеку безразлично с экономической точки зрения лететь на самолёте или ехать поездом. Задача № 1.3. Расчёт максимального числа дней ремонта Иванов хочет отремонтировать квартиру. Он может нанять мастеров и заплатить им 15 тыс. р., а может все сделать сам, тогда ремонт будет стоить ему только 5 тыс. р. (цена материалов). Но придется взять отпуск без сохранения заработка. В день он зарабатывает 500 р. Какое максимальное число дней может потратить на ремонт Иванов, чтобы не нести убытки. Пусть x – число дней, потраченных на ремонт. Если Иванов будет делать ремонт сам, то недополученный заработок составит: 500 × х И ремонт обойдётся ему в сумму стоимости материалов и недополученного заработка: 500 × х + 5 000. Чтобы не понести убытки, эта величина должна быть не больше альтернативной стоимости ремонта Иванова - 15 000 р., то есть не больше затрат на оплату труда наёмных мастеров. Составим и решим неравенство: 500 × х + 5 000 ≤ 15 000 500 × х ≤ 10 000 х ≤ 20. Итак, Иванов может потратить на ремонт максимум 20 дней. Задача № 1.4. Построение КПВ На одном поле фермер может произвести 500 т картофеля или 100 т пшеницы, а на другом альтернативная стоимость выращивания 2 т пшеницы равна 5 т картофеля при максимальном производстве картофеля, равном 1000 т. Построить кривую производственных возможностей фермера. Кривая производственных возможностей (КПВ) – это кривая, каждая точка которой показывает максимальные количества двух экономических благ, которые способна произвести экономика страны при полном и эффективном использовании имеющихся ресурсов и текущем уровне технологий. Из условия задачи известно, что на первом поле фермер может произвести либо 500 т картофеля, либо 100 т пшеницы. Для построения кривой производственных возможностей первого поля откладываем по оси ординат (пшеница) максимальное количество выращенной пшеницы, которое производилось бы в экономике, если бы все имеющиеся ресурсы были направлены на производство пшеницы, то есть 100 т. Производство картофеля в этом случае равно нулю. И наоборот, если все имеющиеся ресурсы направлены на производство картофеля, то максимальное количество – 500 т, которое может быть произведено при полном и эффективном использовании имеющихся ресурсов, мы откладываем по оси абсцисс (картофель). Производство пшеницы в этом случае равно нулю. Соединив две эти точки, получим КПВ первого поля. При этом альтернативные издержки (АИ) производства 1 т картофеля – это то количество пшеницы, от выращивания которого фермер вынужден отказаться: 100 / 500 = 0,2 т пшеницы. На втором поле фермер может произвести максимально 1000 т картофеля или 400 т пшеницы, так как альтернативная стоимость выращивания 2 т пшеницы равна 5 т картофеля. Или альтернативные издержки 1 т картофеля равны 2 / 5 = 0,4 т пшеницы. 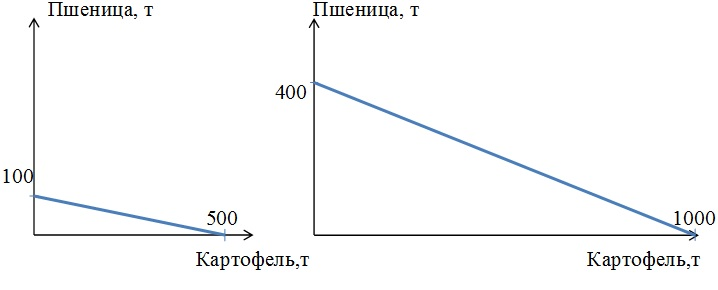 Построим суммарную КПВ для этого фермера. Максимально возможный объём выращиваемой пшеницы – 500 тонн (на первом поле он может вырастить 100 тонн, на втором – 400 тонн). При этом объём картофеля будет нулевым. Отметим соответствующую точку на графике (точка А). Далее определим, на каком из двух полей следует начать выращивать картофель, если фермер решит выращивать хотя бы небольшое его количество. Для этой цели выберем из двух полей то, на котором выращивание каждой единицы картофеля приведёт к наименьшим потерям объёма пшеницы. То есть выберем то поле, где альтернативные издержки выращивания картофеля наименьшие. На первом поле альтернативные издержки 1 т картофеля равны 0,2 т пшеницы. А на втором поле альтернативные издержки 1 т картофеля равны 0,4 т пшеницы. 0,2 меньше, чем 0,4, значит, для производства первых тонн картофеля выгоднее использовать первое поле. Максимально на первом поле можно вырастить 500 т картофеля, пожертвовав при этом 100 тонн пшеницы. Координаты точки перелома (точки В) – 500 тонн картофеля, 400 тонн пшеницы. Максимальное количество картофеля, которое можно вырастить на двух полях равно 1500 тонн (500 тонн на первом поле и 1000 тонн на втором). При этом объём пшеницы будет нулевым. Обозначим точку С на оси абсцисс. Соединив последовательно три точки А, В и С получим суммарную кривую производственных возможностей нашего фермера. 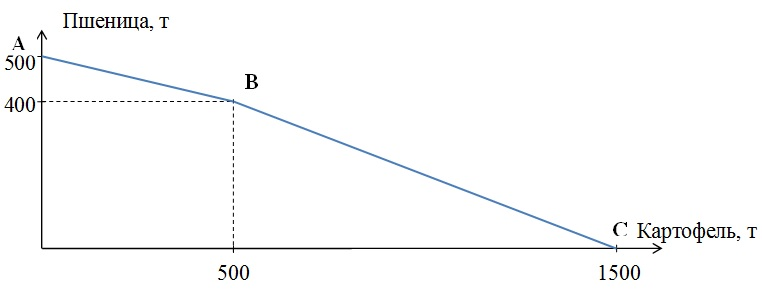 Задача № 1.5. Расчёт альтернативных издержек Средневековый кузнец специализируется на копьях и плугах. Могут ли его альтернативные производственные возможности описываться следующими данными?
При увеличении производства плугов от 0 до 2 необходимо сократить производство копий с 36 до 30. То есть, увеличение производства плугов на 1 единицу требует сокращения копий на 3 единицы: (36 - 30) / (2 - 0) = 3. При увеличении производства плугов от 2 до 5 необходимо сократить производство копий с 30 до 24. То есть, увеличение производства плугов на 1 единицу требует сокращения копий на 2 единицы. А согласно закону возрастающих альтернативных издержек: чтобы получить больше блага одного вида в данный период времени, общество должно жертвовать всё возрастающим количеством другого блага. Значит, при увеличении производства плугов кузнец должен жертвовать всё большим сокращением производства копий. В данном случае наоборот: сокращение произошло в меньшую сторону (2 <3). Следовательно, альтернативные производственные возможности кузнеца описываться такими данными не могут. |
