Кластерный анализ. Практическое задание. Кластерный анализ вариант 3. Практическое задание. Прогнозирование экономических явлений. Задание

• Название: Практическое задание. Прогнозирование экономических явлений. Задание
• Анкор: Кластерный анализ
• Дата: 28.03.2023
• Размер: 333.3 Kb.
• Имя файла: Практическое задание. Кластерный анализ вариант 3.docx
• Тип: Документы; #1020329

Практическое задание. «Прогнозирование экономических явлений».

1. 
   Задание
   

Провести классификацию шести объектов, каждый из которых характеризуется двумя признаками. В качестве расстояния между объектами принять , расстояние между кластерами исчислить по принципам:

1. 
   «ближайшего соседа»
   
2. 
   «дальнего соседа».
   

№ п/п	1	2	3	4	5	6
Х1	23,4	17,5	9,7	18,2	6,6	8,0
Х2	9,2	5,2	5,5	9,4	7,6	5,7

• 
  где х1 - объем выпускаемой продукции;
  
• 
  х2 - среднегодовая стоимость основных промышленно-производственных фондов.
  

Зависимость между признаками приведена на рис. 1.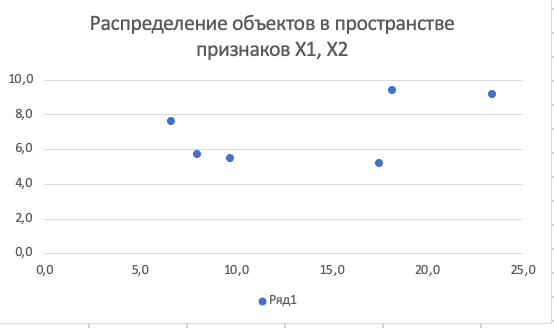

Так как в задаче не обуславливаются единицы измерения признаков, подразумевают, что они совпадают. Следовательно, нет необходимости в нормировании исходных данных, поэтому сразу рассчитываем матрицу расстояний.

2. 
   Порядок выполнения
   

1. 
   Принцип «ближайшего соседа»
   

Создаем таблицу с исходными данными и таблицы (матрицы) с расчетами (табл. 2).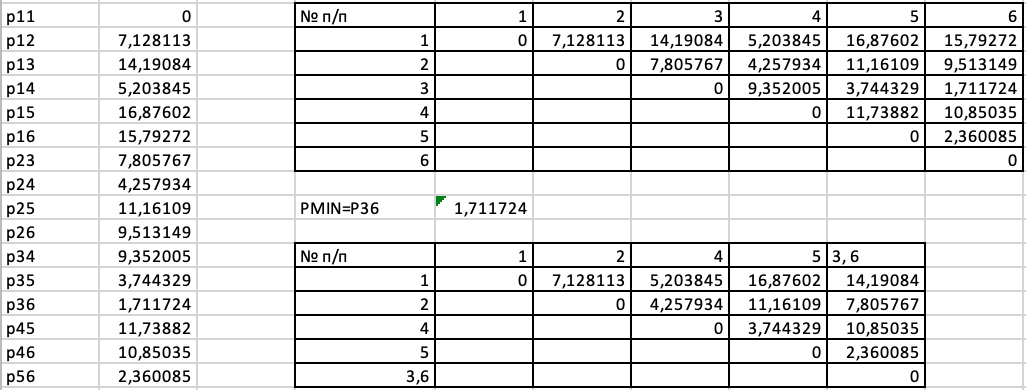


Воспользуемся агломеративным иерархическим алгоритмом классификации.

В качестве расстояния между объектами примем обычное евклидовое расстояние.

Тогда согласно формуле:

,
Полученные данные помещаем в таблицу (матрицу. Из матрицы расстояний следует, что объекты 3 и 6 наиболее близки P36= 1,711724277 и поэтому объединяются в один кластер.
После объединения имеем пять кластеров.

Номер кластера	1	2	3	4	5
Состав кластера	(1)	(2)	(4)	(5)	(3,6)

Вновь находим матрицу расстояний и объединяем объекты 5 и 3,6 имеющие наименьшее расстояние PMIN=P56= 2,360084744.

Номер кластера	1	2	3	4
Состав кластера	(1)	(2)	(4)	(3,6,5)

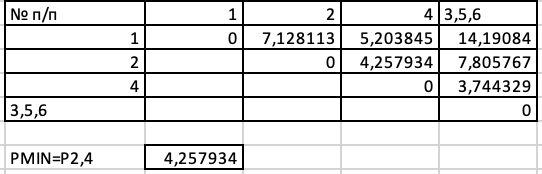Объединим теперь объекты 2,4, расстояние между которыми равно: PMIN=P2,4=4,257933771.

Номер кластера	1	2	3
Состав кластера	(1)	(2,4)	(3,6,5)

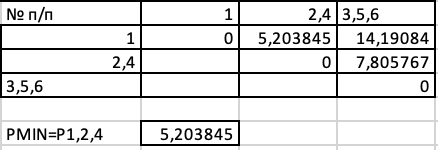Объединим теперь объекты 1,2,4, расстояние между которыми равно: PMIN=P2,4= 5,203844733.

Номер кластера	1	2
Состав кластера	(1,2,4)	(3,6,5)

Таким образом, при проведении кластерного анализа по принципу “ближайшего соседа” получили два кластера: S(1,2,4), S(3,5,6), расстояние между которыми равно:

P(1,2,4); (3,5,6) = 7,8057671.
Результаты иерархической классификации объектов представлены на рис.2 в виде дерева объединения кластеров - дендрограммы, где по оси ординат приводятся расстояния между объединяемыми на данном этапе кластерами.

2. 
   Принцип «дальнего соседа»
   

Расчеты расстояний  Аналогичны предыдущему принципу.

Полученные данные помещаем в таблицу (матрицу). Из матрицы расстояний следует, что объекты 4 и 5 имеют наименьшее значение P36= 1,711724277 и поэтому объединяются в один кластер.

После объединения имеем пять кластеров.

Для решения задачи воспользуемся принципом «дальнего соседа»: искомое расстояние между кластерами S(3), S(6)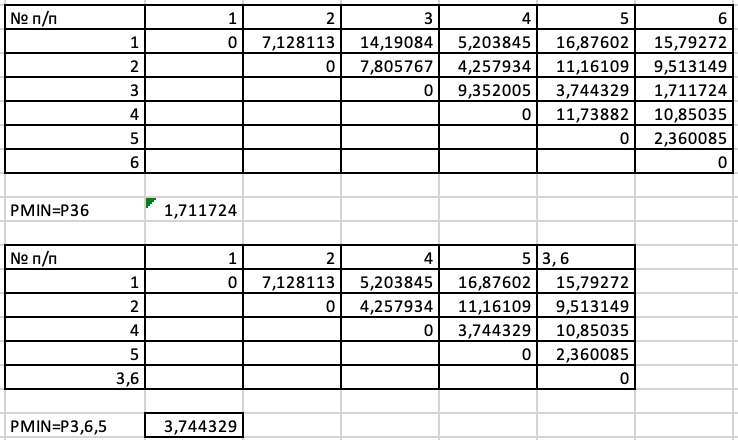



Для расчета расстояния применим формулу, получив расстояние PMIN=P3,6,5= 3,744329045. Объединяем кластеры 5 и 3.6 в один.

Номер кластера	1	2	3	4
Состав кластера	(1)	(2)	(4)	(3,6,5)

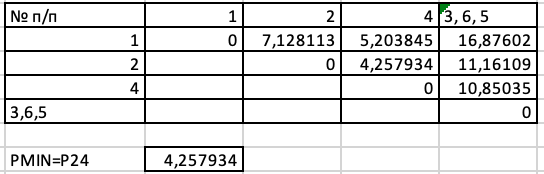Объединим теперь объекты 2,4, расстояние между которыми равно: PMIN=P2,4= 4,257933771.

Номер кластера	1	2	3
Состав кластера	(1)	(2,4)	(3,6,5)

Объединим теперь объекты 1,2,4, расстояние между которыми равно: PMIN=P2,4= 7,128113355.

Номер кластера	1	2
Состав кластера	(1,2,4)	(3,6,5)

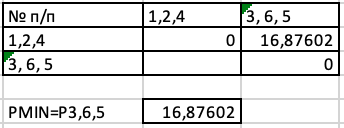Таким образом, при проведении кластерного анализа по принципу “ближайшего соседа” получили два кластера: S(1,2,4), S(3,5,6), расстояние между которыми равно:

P(1,2,4); (3,5,6) = 16,87601849.