Практическое задание. Раздел элементы теории графов
 Скачать 48.35 Kb.
|
|
ПРАКТИЧЕСКОЕ ЗАДАНИЕ. РАЗДЕЛ 2. Элементы теории графов Указание. Выполнить самостоятельно, вручную, на бумаге ручкой. Фотографии решений вставить в данный файл. Переименовать файл Дискр_матем_ПЗ_2_<Группа>_<Фамилия> 1. Используя представленную ниже матрицу смежности вершин для неориентированного графа, ответить на следующие вопросы, не производя построение самого графа: а) для каждой вершины вычислить ее степень; б) для каждой вершины выписать ее множество смежности; в) определить, имеются ли в рассматриваемом графе петли и кратные ребра.  2. В матрице смежности ориентированного графа с 10-ю вершинами элементы 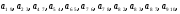  равны 1, остальные элементы равны 0. Построить эту матрицу. Определить:1) Полустепени исхода и захода  , множества смежности  .2) Наличие петель и кратных ребер. 3) Для каждой вершины графа множество достижимости. 4) Компоненты сильной связности графа. Построить геометрическую реализацию исходного графа и его конденсацию. 3. Для графа, изображенного на рисунке, определить с помощью алгоритма Дейкстры кратчайшие маршруты, связывающие вершину 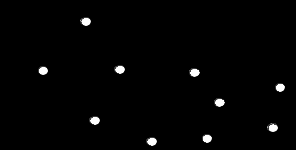 с остальными вершинами графа. 4. Дан двоичный код некоторого дерева:  . Постройте его геометрическую интерпретацию. Задайте данное дерево с помощью кода Прюфера. Добавьте к данному дереву несколько ребер так, чтобы получился эйлеров граф. Предъявите эйлеров цикл в данном графе. Постарайтесь обойтись добавлением как можно меньшего количества ребер. |