Лаба 12 по ОТЭПиВ. Практикум 12 измерение сопротивления нагрузки и настройка волноводной линии в режим бегущей волны москва 2022
 Скачать 2.81 Mb. Скачать 2.81 Mb.
|
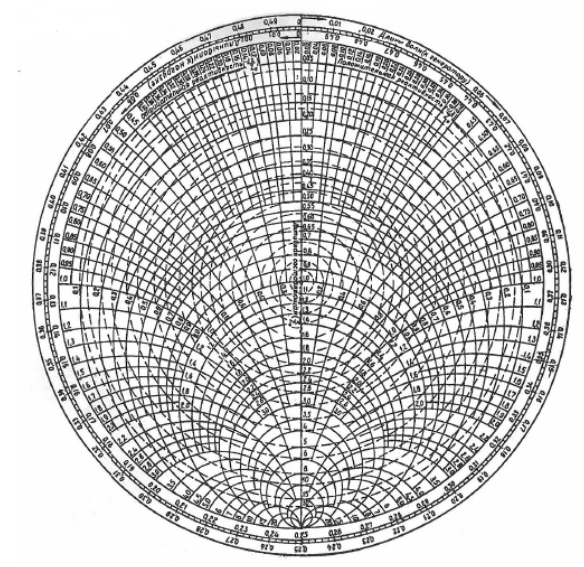 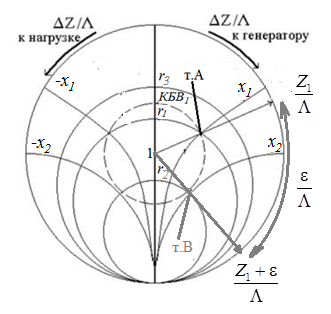 Рисунок 11 Рисунок 12 На круговой диаграмме полных сопротивлений нанесено три семейства кривых, внешняя окружность с указанием направления пересчета и один вертикальный отрезок (см. рисунок 11, а также литературу [2, 3]). Для большей наглядности на рисунке 12 приведены некоторые из этих семейств: Вертикальный отрезок чисто активных сопротивлений (проводимостей) (x=0). На этом отрезке в логарифмическом масштабе откладываются числа, причем центром отрезка (центром круговой диаграммы) является число 1, верхнем концом отрезка 0, а нижнем  . В нашем примере, изображенном на рисунке 12 на этом отрезке отложены четыре числа r1, r2, КБВ1, r3 . В нашем примере, изображенном на рисунке 12 на этом отрезке отложены четыре числа r1, r2, КБВ1, r3 Семейство сплошных окружностей r=const с центрами на вертикальной оси. Эти окружности получили названия окружности равных активных сопротивлений (проводимостей). Любая точка, лежащая на этой окружности, имеет постоянное активное сопротивление (проводимость). На рисунке 12 указаны три таких окружности с постоянным сопротивлением r1, r2, r3. Семейство пунктирных окружностей  с центром в середине вертикального отрезка чисто активных сопротивлений. Эти окружности получили название окружностей равного КБВ. Любая точка, лежащая на этой окружности, имеет постоянный КБВ. На рисунке 12. указана одна из этих окружностей с КБВ=КБВ1. Для определения величины этого КБВ достаточно найти координату пересечения этой окружности с верхней частью вертикального отрезка. Координата пересечения окружности постоянного КБВ с нижней частью вертикального отрезка определяет величину коэффициента стоячей волны (КСВ), который равен 1/КБВ. с центром в середине вертикального отрезка чисто активных сопротивлений. Эти окружности получили название окружностей равного КБВ. Любая точка, лежащая на этой окружности, имеет постоянный КБВ. На рисунке 12. указана одна из этих окружностей с КБВ=КБВ1. Для определения величины этого КБВ достаточно найти координату пересечения этой окружности с верхней частью вертикального отрезка. Координата пересечения окружности постоянного КБВ с нижней частью вертикального отрезка определяет величину коэффициента стоячей волны (КСВ), который равен 1/КБВ.Семейство дуг окружностей x=const, имеющих общую точку в нижнем конце вертикального отрезка. Эти дуги получили название дуги равных реактивных сопротивлений (проводимостей). Любая точка, лежащая на этой дуге, имеет постоянное реактивное сопротивление (проводимость). Дуги, соответствующие положительным значениям x находятся справа от отрезка чисто активных сопротивлений, а дуги, соответствующие отрицательным значениям x слева. На рисунке 12 представлены две дуги с положительным реактивным сопротивлением х1, x2, и две дуги с отрицательными реактивными сопротивлениями -х1,-x2 . Для определения конкретной величины реактивного сопротивления дуги необходимо определить координату пересечения дуги с внешним кругом круговой диаграммы. Внешняя окружность, по которой откладывается расстояние пересчета 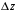 сопротивлений (проводимостей) и направление пересчета (к генератору по часовой стрелке, к нагрузке против часовой стрелки, как показано на рисунке 12). Так как круговая диаграмма используется для пересчета сопротивлений (проводимостей) для различных линий, работающих в разных частотных диапазонах, величины начальной координаты сопротивлений (проводимостей) и направление пересчета (к генератору по часовой стрелке, к нагрузке против часовой стрелки, как показано на рисунке 12). Так как круговая диаграмма используется для пересчета сопротивлений (проводимостей) для различных линий, работающих в разных частотных диапазонах, величины начальной координаты 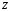 и расстояние пересчета и расстояние пересчета 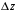 на круговой диаграмме указывается в долях длины волны в линии на круговой диаграмме указывается в долях длины волны в линии 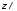 λ и λ и 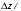 λ. Верхняя точка внешней окружности располагается в верхнем конце вертикального отрезка и соответствует нормированной координате λ. Верхняя точка внешней окружности располагается в верхнем конце вертикального отрезка и соответствует нормированной координате 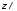 λ=0, нижняя точка внешней окружности совпадает с нижним концом вертикального отрезка и соответствует координате λ=0, нижняя точка внешней окружности совпадает с нижним концом вертикального отрезка и соответствует координате 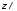 λ λ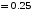 . После перехода через нижнюю точку окружности пересчета идет дальнейший рост нормированной координаты и по достижению полного круга координата проходит путь 0.5λ, что вытекает из свойств периодичности эквивалентного сопротивления (проводимости). . После перехода через нижнюю точку окружности пересчета идет дальнейший рост нормированной координаты и по достижению полного круга координата проходит путь 0.5λ, что вытекает из свойств периодичности эквивалентного сопротивления (проводимости).Таким образом, каждой точке на круговой диаграмме соответствует единственное. Вполне определенное значение комплексного сопротивления, определяемого точкой пересечения линий b) и d). Например, если на круговой диаграмме нужно отобразить комплексное нормированное сопротивление z1=r1+ix1 необходимо найти пересечение окружности r=r1и дугиx=x1 . Пересечение этой окружности и дуги есть точка А, показанная на рисунке 12 и именно эта точка символизирует сопротивление z1=r1+ix1.Отметим, что принципы отображения комплексных величин на круговой диаграмме одинаковы для сопротивлений и проводимостей, поэтому точка А отображает и комплексную нормированную проводимость y1, численно совпадающую с комплексным нормированным сопротивлением z1. Пересчет эквивалентных сопротивлений (проводимостей) по круговой диаграмме выполняется предельно просто. Допустим необходимо пересчитать эквивалентное нормированное сопротивление z1 (точка А) на расстояние 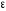 в сторону к генератору. Для этого выполняются следующие операции: в сторону к генератору. Для этого выполняются следующие операции:Из центра круговой диаграммы (точка 1) проводится отрезок, проходящий через точку А и оканчивающийся на внешний окружности. На конце отрезка, в точке на внешней окружности определяется нормированная координата 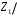 λ (см. рисунок 12). λ (см. рисунок 12).В направлении пересчета, в нашем случае по часовой стрелке, т.к. пересчет идет по направлению к генератору, по внешней окружности откладывается величина 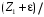 λ. Если бы требовался пересчет в сторону нагрузки, процедура была бы аналогична, но величина λ. Если бы требовался пересчет в сторону нагрузки, процедура была бы аналогична, но величина 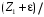 λ откладывалась против часовой стрелки. λ откладывалась против часовой стрелки.Из центра круговой диаграммы проводится отрезок, оканчивающийся в точке на внешней окружности с координатой Находится пересечение этого отрезка с окружностью равного КБВ, на которой располагается точка А. Это пересечение обозначаем как точка В (см. рисунок 12). Точка В и есть пересчитанное значение сопротивления z1в сторону к генератору на расстояние 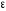 . Назовем это сопротивление z2. . Назовем это сопротивление z2.По круговой диаграмме определяем численные значения активной и реактивной части сопротивления точки В. Как видно из рисунка 12 точка В лежит на пересечении окружности r=r2и дугиx=x2. Соответственно, сопротивлениеz2= r2 +ix2 . Таким образом, если известно хотя бы одно эквивалентное сопротивление (проводимость) в каком-либо сечении линии, с помощью круговой диаграммы легко найти эквивалентное сопротивление (проводимость) в любом другом сечении. Как правило, сначала определяют сопротивление нагрузки, т.е. эквивалентное сопротивление в сечении z=0. Для этого производят два опыта, структурная схема, которых показана на рисунок 13 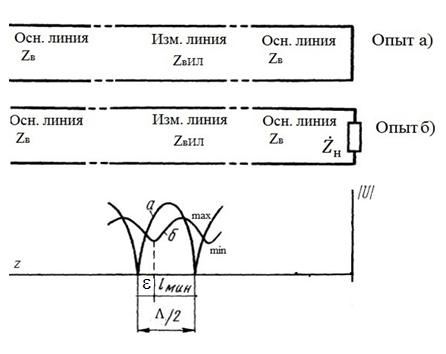 Рисунок 13 В опыте короткого замыкания (опыт а) определяется положение двух соседних узлов амплитуды напряжения, находящегося в пределах рабочего участка измерительной линии, и таким образом измеряется длина волны 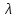 . Далее подключается нагрузка (опыт б) и определяется отношение минимальной к максимальной амплитуде напряжения - КБВ, а также местоположение одного, абсолютно любого, минимума напряжения, находящегося в пределах рабочего участка измерительной линии. После этого определяется смещение узла в опыте б) относительно любого из двух найденных в опыте а) узлов напряжения . Далее подключается нагрузка (опыт б) и определяется отношение минимальной к максимальной амплитуде напряжения - КБВ, а также местоположение одного, абсолютно любого, минимума напряжения, находящегося в пределах рабочего участка измерительной линии. После этого определяется смещение узла в опыте б) относительно любого из двух найденных в опыте а) узлов напряжения  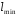 или или 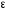 . Как правило, величина смещения определяется меньшой среди величин . Как правило, величина смещения определяется меньшой среди величин 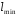 или или 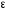 . На рисунке 13 это величина . На рисунке 13 это величина 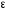 . Поскольку нормированное сопротивление в узле при опыте КЗ равно 0, что совпадает с нагрузкой опыта а), делается вывод что расстояние от нагрузки до узла опыта а) равняется целому числу полуволн. Тогда нормированное сопротивление в том же самом сечении, но уже при опыте б) будет равно нормированному сопротивлению нагрузки и, следовательно, необходимо пересчитать нормированное сопротивление из минимума напряжения в опыте б) в то сечение где в опыте КЗ был узел напряжения, т.е. на величину . Поскольку нормированное сопротивление в узле при опыте КЗ равно 0, что совпадает с нагрузкой опыта а), делается вывод что расстояние от нагрузки до узла опыта а) равняется целому числу полуволн. Тогда нормированное сопротивление в том же самом сечении, но уже при опыте б) будет равно нормированному сопротивлению нагрузки и, следовательно, необходимо пересчитать нормированное сопротивление из минимума напряжения в опыте б) в то сечение где в опыте КЗ был узел напряжения, т.е. на величину 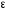 . Так как эквивалентное нормированное сопротивление в узле амплитуды напряжения чисто активно и равно КБВ [2, 3], то нормированное сопротивление нагрузки может быть определено как . Так как эквивалентное нормированное сопротивление в узле амплитуды напряжения чисто активно и равно КБВ [2, 3], то нормированное сопротивление нагрузки может быть определено как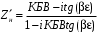 , (5) , (5)где знак “-“ указывает что направление пересчета противоположно направлению смещения  . Наиболее просто определение нормированного сопротивления нагрузки, как частный случай использования формулы пересчета, может быть проведено с помощью круговой диаграммы, как показано на рисунке 14. . Наиболее просто определение нормированного сопротивления нагрузки, как частный случай использования формулы пересчета, может быть проведено с помощью круговой диаграммы, как показано на рисунке 14.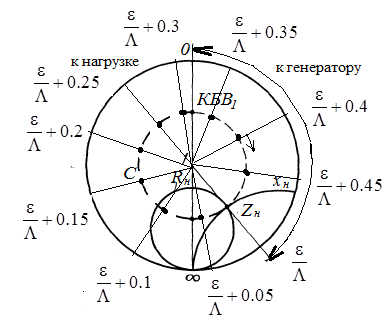 Рисунок 14 Допустим, при подключении нагрузки узел амплитуды напряжения сместился на величину 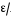 λ в сторону к нагрузки, а величина КБВ составила КБВ1. Тогда для нахождения сопротивления нагрузки и эквивалентных сопротивлений, в сечениях отстоящих от нагрузки на заданное расстояние, необходимо выполнить следующие операции, схематично показанные на рисунке 14. λ в сторону к нагрузки, а величина КБВ составила КБВ1. Тогда для нахождения сопротивления нагрузки и эквивалентных сопротивлений, в сечениях отстоящих от нагрузки на заданное расстояние, необходимо выполнить следующие операции, схематично показанные на рисунке 14.Поскольку узел в режиме подключения нагрузки сместился в сторону к нагрузке относительно опыта КЗ, а пересчет сопротивления производится из узла в режиме подключения нагрузки в узел опыта КЗ (см. рисунок 13) на круговой диаграмме в сторону противоположную смещению узла, в нашем примере в сторону генератора, по внешнему кругу откладывается величина 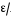 λ. λ.Из центра круговой диаграммы в точку, отложенную на внешнем круге в п.1 проводится отрезок. Также на круговой диаграмме находится пунктирная окружность постоянного КБВ=КБВ1. Пересечение этой окружности и отрезка и есть точка сопротивления нагрузки Zн. Для нахождения эквивалентных сопротивлений с шагом 0.05 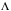 , как требуется в задании к расчетной части, из центра круговой диаграммы в сторону к генератору проводятся вспомогательные отрезки соединяющие центр круговой диаграммы и точки на внешнем круге с координатами , как требуется в задании к расчетной части, из центра круговой диаграммы в сторону к генератору проводятся вспомогательные отрезки соединяющие центр круговой диаграммы и точки на внешнем круге с координатами 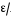 λ+n∙0.05λ, где λ+n∙0.05λ, где 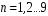 . Полученные точки пересечения этих отрезков с пунктирной окружностью постоянного КБВ=КБВ1 и есть эквивалентные сопротивления в соответствующем сечении (см. рисунок 14). Например, точка С на рисунке 14 соответствует эквивалентному сопротивлению в сечении отстоящим от нагрузки на . Полученные точки пересечения этих отрезков с пунктирной окружностью постоянного КБВ=КБВ1 и есть эквивалентные сопротивления в соответствующем сечении (см. рисунок 14). Например, точка С на рисунке 14 соответствует эквивалентному сопротивлению в сечении отстоящим от нагрузки на 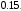 λ. λ.Полученные значения сопротивления нагрузки и эквивалентных сопротивлений объединяются в одну таблицу, после чего строится график, согласно требованиям пункта 2 задания к расчетной части. П.3 КОМПЕНСАЦИОННЫЙ МЕТОД НАСТРОЙКИ ЛИНИИ В РЕЖИМ БЕГУЩЕЙ ВОЛНЫ Существует несколько методов согласования нагрузки с Zв линии [1-3]. В данной лабораторной работе используется метод, предложенный Татариновым [2, 3]. Идея метода состоит в следующем. Если линия нагружена на сопротивление, не равное Zв, появится отраженная волна. При правильном выборе места включения и величины реактивного сопротивления (проводимости) этого элемента поле отраженной от него волны будет равно по амплитуде и противоположно по фазе, поля отраженному от нагрузки. В результате отраженные волны скомпенсируют друг друга (отсюда и название метода) и в линии от генератора до места включения согласующего элемента будет только бегущая волна. Идею настройки линии в режим бегущей волны можно объяснить также пользуясь понятиями эквивалентных сопротивлений и проводимостей. Эквивалентная нормированная проводимость линии Y’(z)=1/Z’(z)=g(z)+ib(z) согласно (2) представляет собой периодическую функцию с периодом 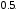 λ. Как видно из рисунка 15 на протяжении половины длины волны существуют два сечения в линии, где активная часть нормированной проводимости g(z)=1. В сечении “А” эквивалентная проводимость линии имеет емкостной характер (b1>0), а в сечении “Б” индуктивный (b2<0). Если в сечении “А” включить параллельно чисто индуктивное сопротивление c отрицательной проводимостью –b1, то суммарная проводимость в сечении “A” будет чисто активной и равной 1 (g1=1). Тогда на участке от генератора до места включения реактивности будет только бегущая волна. Аналогично можно добиться настройки линии в режим бегущей волны и в сечении “Б”, где согласующий элемент должен иметь емкостное сопротивление. λ. Как видно из рисунка 15 на протяжении половины длины волны существуют два сечения в линии, где активная часть нормированной проводимости g(z)=1. В сечении “А” эквивалентная проводимость линии имеет емкостной характер (b1>0), а в сечении “Б” индуктивный (b2<0). Если в сечении “А” включить параллельно чисто индуктивное сопротивление c отрицательной проводимостью –b1, то суммарная проводимость в сечении “A” будет чисто активной и равной 1 (g1=1). Тогда на участке от генератора до места включения реактивности будет только бегущая волна. Аналогично можно добиться настройки линии в режим бегущей волны и в сечении “Б”, где согласующий элемент должен иметь емкостное сопротивление. 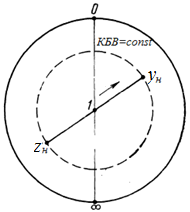 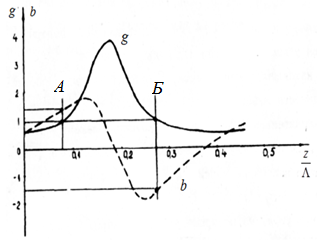 Рисунок 15 Рисунок 16 Положение сечений “А” и “Б” и проводимости согласующих элементов находится по круговой диаграмме следующим образом. Поскольку в этом методе согласующий элемент включается в линию параллельно удобнее пользоваться понятиями эквивалентных проводимостей, поэтому необходимо по заданному нормированному сопротивлению нагрузки Zннайти нормированную проводимость Yн. Для этого на круговой диаграмме откладывается точка Zн по правилам описанным в приложении 2. Затем через эту точку проводится пунктирная окружность КБВ=const. Отрезок, соединяющий центр круговой диаграммы и точку Zн, поворачивается на 1800, что соответствует пересчету на λ/4 по круговой диаграмме. Точка пересечения зеркального отрезка и пунктирной окружности и есть Yн. Вся процедура нахождения Yн показана на рисунке 16. На рисунке 17 показано нахождение место включения (  λ) согласующего элемента и определение величин проводимости согласующих элементов при его включении в сечение “А” и “Б” с помощью круговой диаграммы. λ) согласующего элемента и определение величин проводимости согласующих элементов при его включении в сечение “А” и “Б” с помощью круговой диаграммы.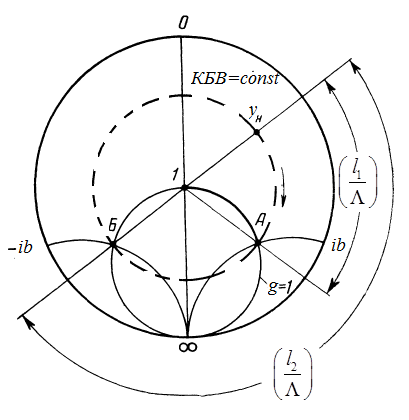 Рисунок 17 Поскольку активная проводимость линии путем параллельного включения реактивного согласующего элемента изменена быть не может, очевидно, что согласующий элемент может быть помещен только в то сечение линии, где нормированная активная проводимость линии равна 1. На круговой диаграмме имеется две точки (А и Б) пересечения пунктирной окружности КБВ=const c окружностью равных активных проводимостей g=1. Расстояние от нагрузки до точки А (  λ) определяется на внешнем круге по часовой стрелке, поскольку согласующее устройство включается перед нагрузкой, т.е. ближе к генератору. Аналогично определяется и расстояние до точки Б ( λ) определяется на внешнем круге по часовой стрелке, поскольку согласующее устройство включается перед нагрузкой, т.е. ближе к генератору. Аналогично определяется и расстояние до точки Б ( λ). При включении согласующего элемента в сечение “А” его реактивная проводимость должна компенсировать реактивную проводимость линии в точке А. Как мы видим по рисунку 17 реактивная проводимость в точке А положительна ( λ). При включении согласующего элемента в сечение “А” его реактивная проводимость должна компенсировать реактивную проводимость линии в точке А. Как мы видим по рисунку 17 реактивная проводимость в точке А положительна (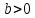 ) поэтому согласующий элемент должен иметь отрицательную реактивность ) поэтому согласующий элемент должен иметь отрицательную реактивность 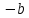 что соответствует индуктивной диафрагме. При включении согласующего элемента в сечение “Б” реактивная проводимость отрицательна ( что соответствует индуктивной диафрагме. При включении согласующего элемента в сечение “Б” реактивная проводимость отрицательна (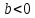 ), поэтому наш согласующий элемент должен иметь положительную проводимость ), поэтому наш согласующий элемент должен иметь положительную проводимость 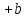 , что соответствует емкостному штырю. , что соответствует емкостному штырю. |
