Лаба 12 по ОТЭПиВ. Практикум 12 измерение сопротивления нагрузки и настройка волноводной линии в режим бегущей волны москва 2022
 Скачать 2.81 Mb. Скачать 2.81 Mb.
|
|
Измерение проводимости нагрузки Замените короткозамыкающую пластину на выходе волновода на согласованную нагрузку с диафрагмой (рисунок 8), для этого на выход волновода вначале необходимо установить диафрагму, а затем приставить нагрузку и зафиксировать это положение зажимом.  Рисунок 8 – Установка нагрузки на волновод Выведите емкостной штырь. Запишите значение маркера на центральной частоте в виде комплексного числа 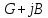 . Полученное значение будет равно проводимости нагрузки в сименсах (См). Переведите проводимость нагрузки в нормированный вид, для этого необходимо умножить действительную и мнимую части на 50 Ом. . Полученное значение будет равно проводимости нагрузки в сименсах (См). Переведите проводимость нагрузки в нормированный вид, для этого необходимо умножить действительную и мнимую части на 50 Ом.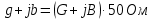 Пример расчета: 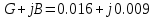 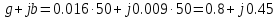 Определение места включения согласующего элемента По найденной в предыдущем пункте нормированной проводимости нагрузки с помощью круговой диаграммы необходимо определить сечение линии, в которое нужно будет ввести емкостной штырь для настройки волновода в режим бегущей волны. Найдите на диаграмме точку пересечения линий активной 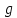 и реактивной и реактивной 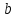 составляющих нормированной проводимости и определите по этой точке КБВ и сечение, в котором находится нагрузка (рисунок 9). Место включения согласующего емкостного штыря расположено на левой половине круговой диаграммы (см. Приложение П.3) в точке пересечения окружности КБВ и окружности единичной активной проводимости. составляющих нормированной проводимости и определите по этой точке КБВ и сечение, в котором находится нагрузка (рисунок 9). Место включения согласующего емкостного штыря расположено на левой половине круговой диаграммы (см. Приложение П.3) в точке пересечения окружности КБВ и окружности единичной активной проводимости. 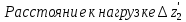 Рассчитайте положение места включения в обоих направлениях – к генератору 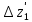 и к нагрузке и к нагрузке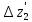 , как показано на рисунке 9. , как показано на рисунке 9.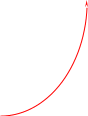            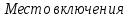 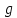 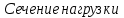 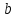 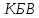 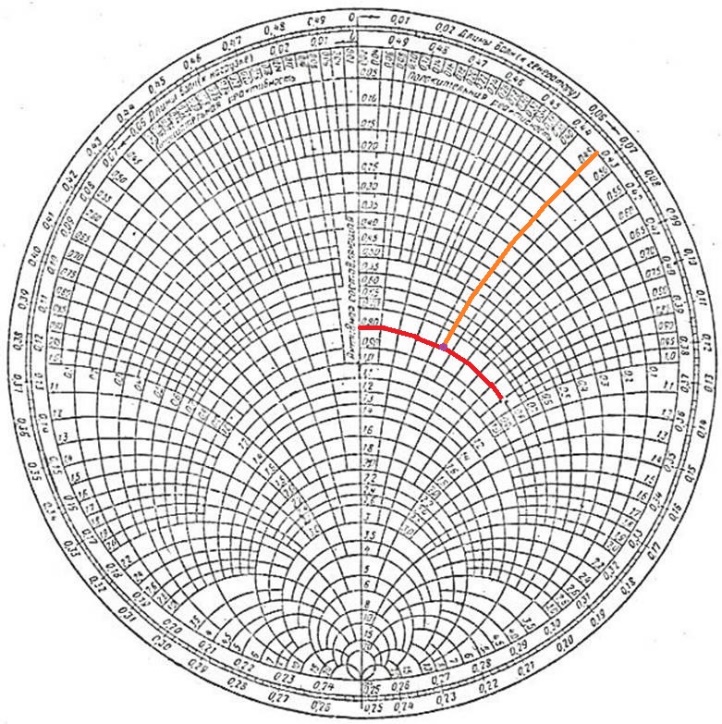  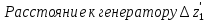 Рисунок 9 – Определение места включения согласующего элемента Нормированные безразмерные расстояния 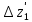 и и 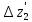 переведите в единицы длины, для этого их нужно умножить на длину волны в волноводе , найденную в пункте 3. переведите в единицы длины, для этого их нужно умножить на длину волны в волноводе , найденную в пункте 3.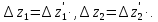 График»'>Настройка волновода в режим бегущей волны Для дальнейших измерений необходимо добавить второй график. Нажмите на правой панели кнопку «График», в появившемся диалоговом окне «График» щелчком левой кнопки мыши по полю «Добавить график». На экране появится график Гр2. Для изменения формата графика нажмите на правой панели кнопку «График» (см. рисунок 6). В появившемся диалоговом окне «График» щелчком левой кнопки мыши по полю «Формат» вызовите диалоговую форму для выбора формата графика. В диалоговом окне «Формат» из списка выберите строку «КСВН» и завершите выбор нажатием на кнопку «ОК». Добавьте маркер на второй график с помощью кнопки В диалоговом окне «График» нажмите кнопку «Размещение графиков», выберите верхнее среднее размещение Передвиньте штырь согласующей секции по горизонтальной шкале из точки z0, найденной в пункте 4, на найденное в пункте 6 расстояние 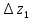 к генератору (влево) или на расстояние к генератору (влево) или на расстояние 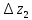 к нагрузке (вправо). к нагрузке (вправо).Введите штырь. Постепенно увеличивая глубину погружения штыря (закручиванием), настройте линию на бегущую волну. Если место включения определено правильно, то при плавном введении штыря КСВ на втором графике должен уменьшаться. Линия считается настроенной в режим бегущей волны если КСВ < 1,05. Запишите в отчет полученное значение КСВ, координату места включения на шкале согласующей секции и глубину погружения штыря. Работа в частотном диапазоне Для исследования диапазона согласования потребуется добавить второй маркер на график 2 (Гр2). Маркер добавляется с помощью кнопки Для автоматического вычисления полосы частот можно воспользоваться специальной функцией программы. Нажмите программные кнопки: Маркер > Вычисления (Математика) > Статистика > Статистика (Вкл.) > Диапазон статистики (Вкл.). Ширину частотного диапазона показывает параметр 1–2. 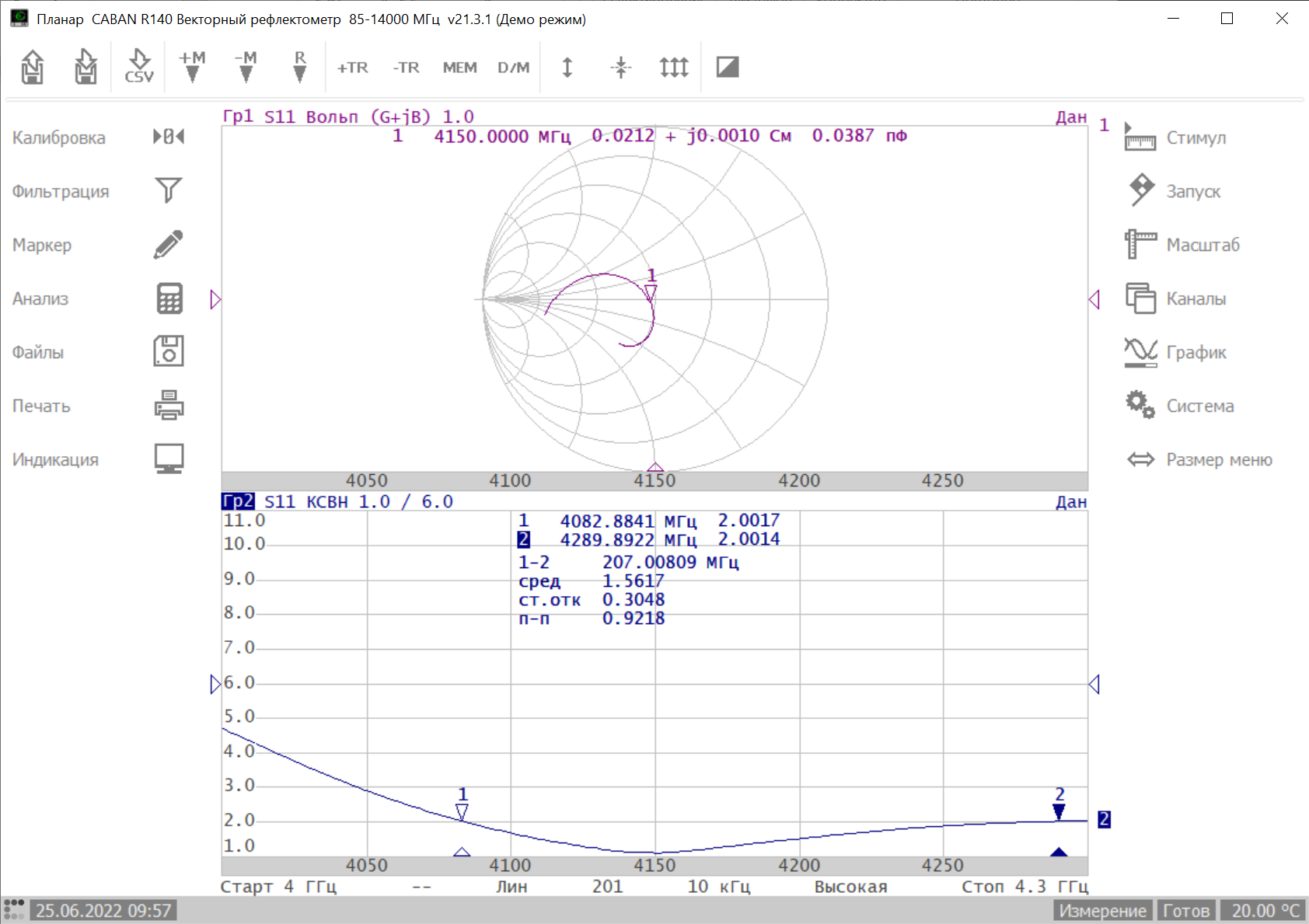 Рисунок 10 – Измерение диапазона согласования Запишите в отчет ширину частотного диапазона 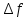 в МГц. в МГц.Переведите ширину диапазона в проценты: 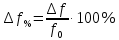 , где , где 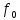 – заданная центральная частота из Таблицы 2. – заданная центральная частота из Таблицы 2.Изменяя глубину погружения штыря необходимо добиться максимально возможной ширины частотного диапазона. При измерении необходимо корректировать положения маркеров 1 и 2, так чтобы они всегда оставались на уровне КСВ 2. Запишите в отчет полученную ширину диапазона (в МГц и в %), глубину погружения штыря и минимальное значение КСВ. На этом выполнение лабораторной работы завершено. Закройте окно программы RVNA. Завершите работу компьютера. Отсоедините кабель USB рефлектометра. Разберите измерительный тракт, отсоединив нагрузку, выведя штырь и установив секцию на 0. Содержание отчета 1. Цель работы. 2. Результаты домашнего расчета. 3. Значения величин, полученных экспериментально. 4. Краткие выводы по работе. Контрольные вопросы Что такое коэффициент отражения, коэффициент бегущей волны и коэффициент стоячей волны и от чего они зависят? Включению какой нагрузки эквивалентно присоединение короткозамкнутого отрезка линии длиной? Куда сдвигается минимум амплитуды напряжения в линии по сравнению с ближайшим узлом при КЗ при чисто емкостной нагрузке на конце линии? Объяснить результат. То же самое, что в п.3, но при чисто индуктивной нагрузке. То же самое, что в п.3, но при чисто активной нагрузке. Рассмотреть три случая и для указанных случаев показать зависимость амплитуды напряжения от координаты, изменяющейся вдоль линии. От чего зависит длина волны в волноводе? На основе каких соображений проводится анализ распространения электромагнитных волн в волноводах конечной длины? Что называют входным, нормированным входным, эквивалентным, нормированным эквивалентным и волновым сопротивлением линии передачи? На основе каких соображений вводится понятие длинной линии, эквивалентной волноводу? Как определяется волновое сопротивление волновода? В чем состоит метод измерения сопротивления линии? С какой целью стремятся согласовать сопротивление нагрузки с волновым сопротивлением линии? На основе каких методов может быть решена задача согласования? В чем состоит метод согласования линии с помощью реактивного элемента? В чем состоит метод согласования с помощью четвертьволновой вставки? Как осуществляется широкополосное согласование? Список литературы 1. Седов. В.М, Гайнутдинов Т.А. Электромагнитные поля и волны. – М. Горячая линия Телеком, 2017. с. 210 – 238. 2. Пименов Ю.В., Вольман В.И., Муравцов А.Д. Техническая электродинамика. – М: Радио и Связь, 2000. с. 360 – 388, с. 401 – 407. 3. Сазонов Д.М. Антенны и устройства СВЧ. – М. Высшая школа. 1988. с. 36 – 47. ПРИЛОЖЕНИЯ П.1 ЭКВИВАЛЕНТНОЕ СОПРОТИВЛЕНИЕ ЛИНИИ И ФОРМУЛА ТРАНСФОРМАЦИИ При анализе процессов, происходящих в линиях передачи конечной длины, обычно пользуются методами теории длинных линий, основанных на концепции падающих и отраженных волн. Структура каждой, отдельной падающей или отраженной волны предполагается такой же, как в линии бесконечной длины. Напряжение и ток в длинной линии рассматриваются соответственно как суммы напряжений и токов падающей и отраженной волны 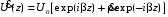 , ,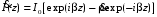 , (1) , (1)где 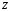 - расстояние от конца линии (нагрузки) до исследуемого сечения линии, - расстояние от конца линии (нагрузки) до исследуемого сечения линии, 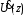 и и 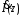 -комплексные амплитуды напряжения и тока в исследуемом сечении, -комплексные амплитуды напряжения и тока в исследуемом сечении, 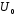 и и 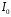 - амплитуды напряжения и тока в падающей волне, - амплитуды напряжения и тока в падающей волне, 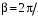 λ- коэффициент фазы, λ- длина волны в линии, λ- коэффициент фазы, λ- длина волны в линии, 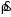 - коэффициент отражения по напряжению. - коэффициент отражения по напряжению.Отношение амплитуд напряжения и тока в бегущей (падающей) волне равно волновому сопротивлению линии 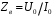 . Отношение комплексных амплитуд напряжения и тока в сечении линии . Отношение комплексных амплитуд напряжения и тока в сечении линии 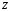 называют эквивалентным сопротивление линии называют эквивалентным сопротивление линии 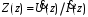 . Эквивалентное сопротивление линии . Эквивалентное сопротивление линии 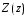 имеет ясный физический смысл. Если обрезать линию в сечении z (от генератора до сечения с координатой z) и нагрузить оставшуюся часть линии на сопротивление нагрузки численно равное имеет ясный физический смысл. Если обрезать линию в сечении z (от генератора до сечения с координатой z) и нагрузить оставшуюся часть линии на сопротивление нагрузки численно равное 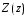 , то распределение амплитуд напряжения и тока в оставшейся части линии останется таким же как и до обрезания. Эквивалентное сопротивление, вычисленное для сечения, соответствующего входу линии ( , то распределение амплитуд напряжения и тока в оставшейся части линии останется таким же как и до обрезания. Эквивалентное сопротивление, вычисленное для сечения, соответствующего входу линии (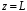 ) называют входным сопротивлением линии ) называют входным сопротивлением линии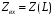 , где , где 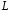 - длина линии. В конце линии (в сечении нагрузки - длина линии. В конце линии (в сечении нагрузки 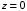 ) эквивалентное сопротивление равно сопротивлению нагрузки ) эквивалентное сопротивление равно сопротивлению нагрузки 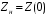 . Очевидно, что эквивалентное сопротивление линии в сечении . Очевидно, что эквивалентное сопротивление линии в сечении 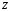 равно входному сопротивлению отрезка линии длиной равно входному сопротивлению отрезка линии длиной 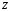 , нагруженного на сопротивление , нагруженного на сопротивление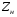 . .Отношение эквивалентного сопротивления к волновому сопротивлению называют нормированным эквивалентным сопротивлением линии 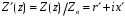 . Соответственно величины . Соответственно величины 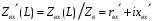 и и 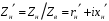 называют нормированным входным сопротивлением линии и нормированным сопротивление нагрузки. Помимо нормированных сопротивлений используют и нормированные проводимости. Нормированная эквивалентная проводимость линии определяется как называют нормированным входным сопротивлением линии и нормированным сопротивление нагрузки. Помимо нормированных сопротивлений используют и нормированные проводимости. Нормированная эквивалентная проводимость линии определяется как 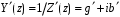 . Нормированная входная проводимость линии и нормированная проводимость нагрузки определяются аналогично . Нормированная входная проводимость линии и нормированная проводимость нагрузки определяются аналогично 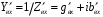 , , 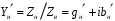 Волновод является одним из видов линии передачи, поэтому полученные в теории длинных линий результаты можно использовать и при рассмотрении волноводов. Во многих случаях, особенно связанных с оценкой эффективности переноса мощности электромагнитного поля по волноводу, оказывается удобным вместо волновода рассматривать эквивалентную ему двухпроводную длинную линию [1, 2]. В волноводной технике стараются пользоваться только нормированными сопротивлениями и проводимостями [1-3]. Из теории длинных линий [1-3] известна формулы, связывающая между собой нормированное эквивалентное сопротивление (проводимость) в сечении 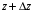 с нормированным эквивалентным сопротивлением (проводимостью) в сечении с нормированным эквивалентным сопротивлением (проводимостью) в сечении 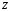 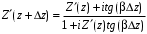 , ,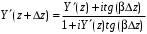 . (2) . (2)Формулы (2) показывают как трансформируется эквивалентное сопротивление (проводимость) вдоль длинной линии, поэтому эти формулы принято называть формулами трансформации. Частным случаем формул трансформации (формул пересчета) является ситуация, когда в качестве начального сечения 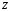 выбирается сечение нагрузки выбирается сечение нагрузки 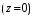 , и формулы (2) приобретают вид , и формулы (2) приобретают вид 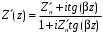 , , 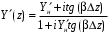 . (3) . (3)Из (2) видно, что 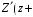 λ λ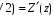 , , 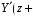 λ λ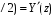 . Отсюда следует, что эквивалентные нормированные сопротивления (проводимости) являются периодическими функциями продольной координаты . Отсюда следует, что эквивалентные нормированные сопротивления (проводимости) являются периодическими функциями продольной координаты 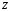 с периодом λ/2, поэтому для полного описания трансформации эквивалентных сопротивлений (проводимостей) вдоль длинной линии достаточно определить эти величины на любом удобном интервале длиной λ/2. Эквивалентные сопротивления (проводимости) связаны с величиной коэффициента отражения с периодом λ/2, поэтому для полного описания трансформации эквивалентных сопротивлений (проводимостей) вдоль длинной линии достаточно определить эти величины на любом удобном интервале длиной λ/2. Эквивалентные сопротивления (проводимости) связаны с величиной коэффициента отражения 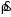 и КБВ следующими соотношениями и КБВ следующими соотношениями 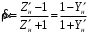 , , 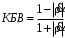 . (4) . (4)П.2 КРУГОВАЯ ДИАГРАММА ПОЛНЫХ СОПРОТИВЛЕНИЙ И ОПРЕДЕЛЕНИЕ СОПРОТИВЛЕНИЯ НАГРУЗКИ Сравнительно высокая трудоемкость вычислений по формулам (2) и (4), необходимых для определения энергетической эффективности процесса переноса мощности по линии передачи привела к созданию специального устройства, необходимого для упрощения расчетов по (2), (4) при сохранении приемлемой с инженерной точки зрения точности. Данное устройство получило название круговая диаграмма полных сопротивлений (диаграмма Вольперта-Смита). В дальнейшем мы не будем использовать термин нормированные сопротивления и проводимости, а просто говорить о сопротивлениях и проводимостях, поскольку круговая диаграмма используют только нормированные величины. Общий вид диаграммы приведен на рисунке 11, а вид в масштабе, достаточном для проведения практических расчетов, в литературе [2, 3]. |
