Механика задание 1. Практикум по дисциплине Механика
 Скачать 266.87 Kb. Скачать 266.87 Kb.
|
 Практикум по дисциплине «Механика» Задача 4.9
Решение: 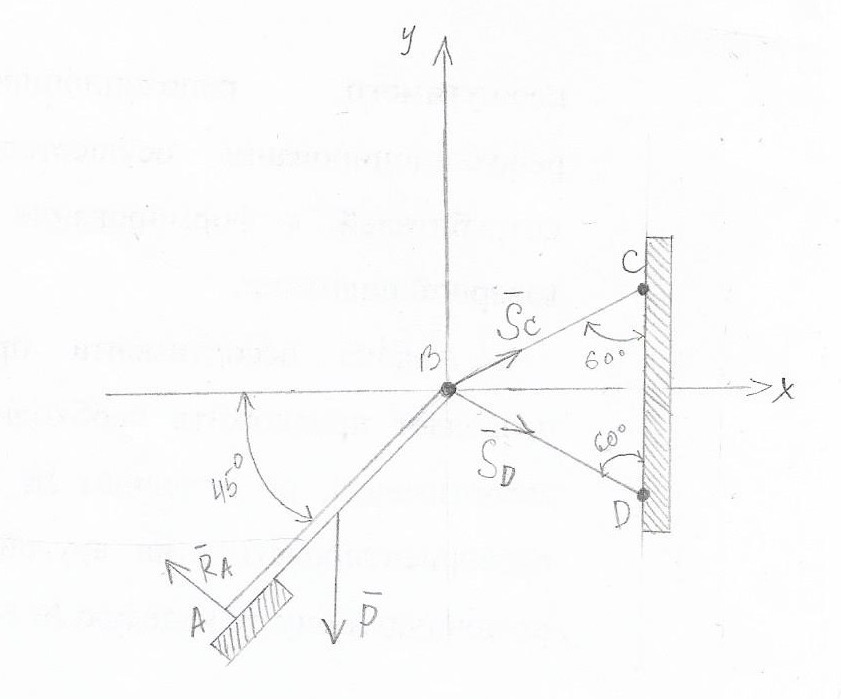 Составим уравнение равновесия: 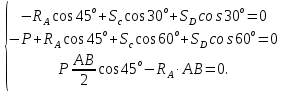 Из третьего уравнения системы вычислим: 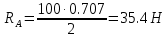 Сложив два первых уравнения системы, получим -P+SC(cos300+cos600)+SD(cos300-cos600)=0 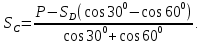 Подставим SC в первое уравнение системы: 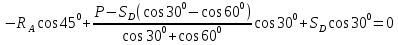 Найдем SD: 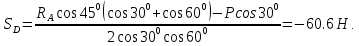 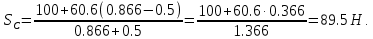 Ответ: 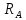 =35,4 Н; =35,4 Н; 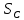 =89,5Н; =89,5Н; 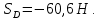  Практикум по дисциплине «Механика» Выполнила: Плотникова А.В. Группа: ЭРТбп-1801а Задача 13.15 Маховое колесо радиуса R= 2 м вращается равноускоренно из состояния покоя; через t= 10 с точки, лежащие на ободе, обладают линейной cкоростью v=100 м/с. Найти скорость, нормальное и касательное ускорение точек обода колеса для момента t= 15 с.
Сначала определим параметры движения колеса в момент t=10c. По известнойскорости точки , лежащей на ободе колеса, находим угловую скорость колеса ω. 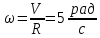 С другой стороны, при равноускоренном вращении колеса состояния покоя его угловая скорость определяется выражением: 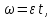 где 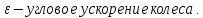 Отсюда при t=10c 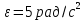 По полученному ускорению колеса 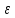 с помощью равенства подсчитываем для момента t=15c угловую скорость колеса с помощью равенства подсчитываем для момента t=15c угловую скорость колеса 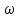 и искомые значения скорости V , вращательного Wвр и осестремительного Wос ускорений точек обода колеса и искомые значения скорости V , вращательного Wвр и осестремительного Wос ускорений точек обода колеса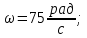 V=150 м/с; ωt = 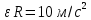 ωn = 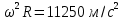 Ответ: V=150 м/с;ωt = 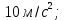 ωn = ωn =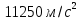 . . Практикум по дисциплине «Механика» Выполнила: Плотникова А.В. Группа: ЭРТбп-1801а Задача 36.9 По горизонтальной платформе A, движущейся по инерции со скоростью v0, перемещается тележка В с постоянной относительной скоростью u0. В некоторый момент времени тележка была заторможена. Определить общую скорость v платформы с тележкой после ее остановки, если M - масса платформы, а m – масса тележки.
Решение: 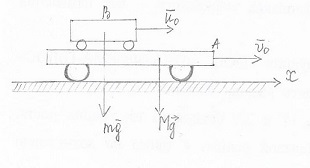 Тележка В совершает сложное движение , ее абсолютная скорость 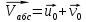 Так как проекция главного вектора внешних сил на ось х равна нулю , можно записать закон сохранения импульса в проекции на эту ось: M(u0+v0)+Mv0=(m+M)v Отсюда: 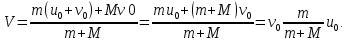 Ответ: 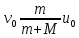 . . Практикум по дисциплине «Механика» Выполнила: Плотникова А.В. Группа: ЭРТбп-1801а Задача 37.13 Часовой балансир А может вращаться вокруг оси, перпендикулярной его плоскости и проходящей через центр тяжести О, имея относительно этой оси момент инерции J. Балансир приводится в движение спиральной пружиной, один конец которой с ним скреплен, а другой присоединен к неподвижному корпусу часов. При повороте балансира возникает момент сил упругости пружины, пропорциональный углу поворота. Момент, необходимый для закручивания пружины на один радиан, равен с. Определить закон движения балансира, если в начальный момент в условиях отсутствия сил упругости балансиру сообщили начальную угловую скорость w0.
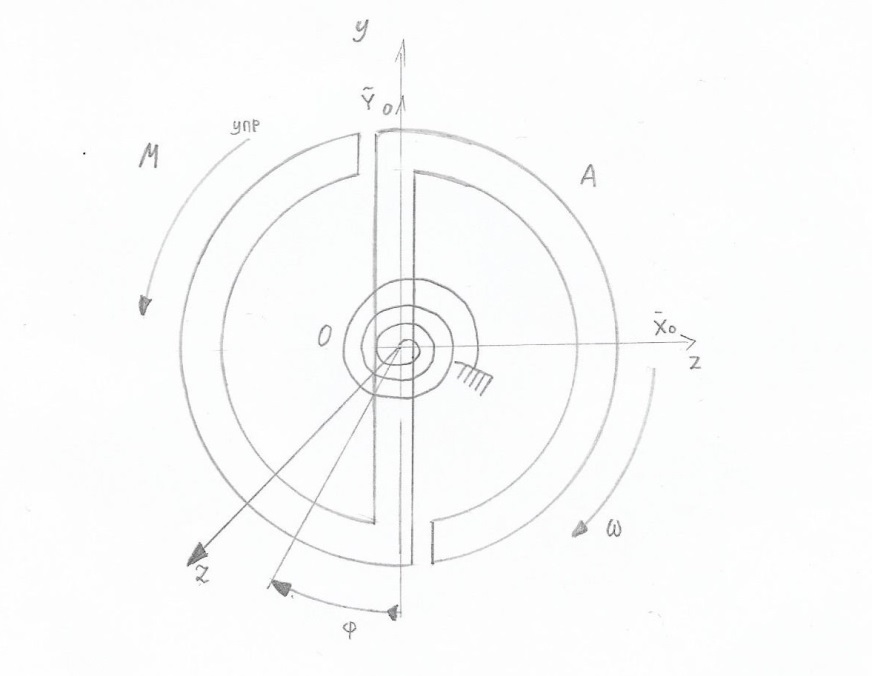 Вращение часового балансира А происходит под действием приложенных к нему сил момента Мупр сил упругости пружины , реакций связей 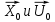 в опоре О. в опоре О.Запишем дифференциальное уравнение вращения твердого тела вокруг неподвижной оси z 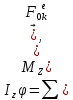 где 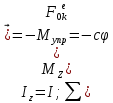 . .Получим однородное дифференциальное уравнение: 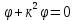 , ,где к= 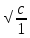 Откуда 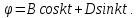 Продифференцируем выражение по времени: 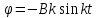 +Dkcoskt. +Dkcoskt.Постоянные интегрированияBиDнайдем из начальных условий: φ0=0, φ0=ω0 приt=0. Тогда B=0, D = 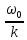 = ω0= = ω0=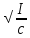 . .С учетом значений B, D и K запишем уравнение движения балансира А: φ=ω0= 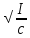 sin sin 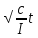 . .Ответ: φ=ω0= 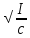 sin sin 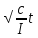 . . |
