Понятие “числа” является одним из основных понятий математики. В процессе своего развития оно расширялось и обобщалось, проходя определенные этапы: целые положительные (натуральные) числа; рациональные (дробные) числа; отрицательные числа; иррациональные числа; действительные числа как совокупность рациональных и иррациональных чисел; комплексные числа.
Прежде всего следует подчеркнуть, что вопрос о кодировании (представлении) чисел в микропроцессорных системах полностью находится в компетенции разработчика программного обеспечения, однако в большинстве случаев целесообразно использовать стандартные формы кодирования, особенно, если приходится применять какие-либо стандартные подпрограммы.
Один и тот же двоичный код может быть интерпретирован различными способами. Так, например, машинное слово в 8-битной микро-ЭВМ может быть интерпретировано как двоичное целое число без знака в диапазоне от 0 до 255, как двоичное целое число со знаком в диапазоне от -128 до +127 или как двоично-десятичное целое число без знака в диапазоне от 0 до 99. Если необходимо работать с числами в более широких диапазонах, то для их представления необходимо использовать два, три или более байтов (машинных слов).
Что касается чисел без знака, то процесс их кодирования заключается в записи числа в двоичной системе счисления с заданным числом разрядов. Например, числу 254 соответствует однобайтный двоичный код 11111110, а числу 8 – код 00001000. Если целое число без знака равно или больше 256, то для его представления в 8-битной микро-ЭВМ требуется несколько машинных слов.
При кодировании чисел со знаком старший (крайний слева) разряд числа отводится под знак: 0 соответствует положительному числу, а 1 – отрицательному. Остальные разряды отводятся под величину числа, при этом для положительных чисел в них так же, как и для чисел без знака, заносится модуль числа в двоичной системе счисления. При кодировании же отрицательных чисел могут быть использованы различные способы.
Наиболее простым является способ представления отрицательных чисел в виде знак-модуль. Отрицательное и положительное числа представляются одинаково, за исключением левого знакового разряда. Такой код называется прямым кодом числа. Например, число +3 в прямом коде (как и в любом другом) выглядит как 00000011, а число -3 как 10000011.Недостаток использования прямого кода состоит в сложности реализации арифметических операций над числами с разными знаками.
Другим способом представления чисел со знаком является использование обратного кода. Для получения обратного кода отрицательного числа берется инверсия его положительного двоичного представления, то есть каждый нуль заменяется на единицу, а каждая единица – на нуль:
+3 = 00000011B; -3 = 11111100B.
Реализация арифметических операций при использовании обратного кода существенно облегчается, однако остаются некоторые недостатки: два различных представления нуля, не эквивалентных по записи; необходимость циклического переноса при сложении для получения правильного результата.
Еще одним способом представления чисел со знаком является дополнительный код. Дополнительный код отрицательного числа равен его обратному коду плюс единица, добавляемая к младшему разряду числа. Например, дополнительный код числа -3 равен 11111101B. При использовании дополнительных кодов операция нахождения двоичного дополнения (операция “инверсия плюс единица”) соответствует изменению знака числа на противоположный.
Полезным также является следующее свойство: число, сложенное со своим дополнением, дает в результате нули во всех разрядах и единицу в разряде переноса. Поэтому двоичное дополнение может быть найдено вычитанием кода исходного числа из числа, содержащего нули во всех используемых разрядах и единицу в следующем разряде. Например, число – 3 можно получить в виде
100000000B – 00000011B = 11111101B.
Сложение и вычитание чисел в дополнительных кодах выполняются предельно просто по сравнению с другими способами кодирования, а также имеется единственное представление нуля. Поэтому именно дополнительный код и используется, как правило, для представления чисел со знаком.
Для представления чисел произвольной величины – не только целых, но и дробных в цифровых устройствах используются две основные формы: с фиксированной и плавающей запятой (точкой).
Ч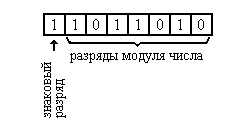
исла с фиксированной запятой. В ячейке для хранения числа с фиксированной запятой один разряд используется в качестве знакового, а остальные разряды используются для хранения величины числа. Запятая, отделяющая целую часть числа от ее дробной части, занимает фиксированное положение: часто перед старшим разрядом, либо после младшего разряда. В первом случае для всех представляемых в этой форме чисел абсолютное значение меньше единицы. Например, число – 0,101101B следующим образом разместится в элементах запоминающей ячейки:
Свободные младшие разряды заполняются нулями. Так как в этом случае предусматривается хранение лишь дробной части числа, то не только исходные данные, но и результаты всех проведенных над ними операций должны быть числами, абсолютное значение которых меньше единицы. Выполнение этого условия обеспечивается выбором определенных масштабных коэффициентов, на которые умножаются исходные данные задачи. Неправильный выбор коэффициентов может вызвать так называемое переполнение разрядной сетки – возникновение ошибки, если в результате выполнения операций в числе образуется целая часть, для хранения которой в разрядной сетке не предусмотрено места, и она теряется.
Необходимость в масштабировании данных составляет один из недостатков представления чисел с фиксированной запятой; другой недостаток этой формы – низкая точность представления чисел, абсолютное значение которых мало (нули в старших разрядах приводят к уменьшению числа разрядов, занимаемых значащей частью числа, и к снижению точности представления числа).
Во втором случае, когда запятая фиксируется после младшего разряда, числа с фиксированной запятой – целые. Например, число 11011B будет размещено в ячейке памяти следующим образом:
З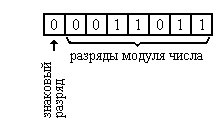
десь свободные старшие разряды заполняются нулями. Если n – число разрядов ячейки, то диапазон модулей представимых в ней целых чисел:
0 ... (2 n –1 – 1).
В принципе положение запятой можно зафиксировать после любого разряда. Количество разрядов слева будет определять максимальную величину целой части, количество разрядов справа – точность представления результата. После выполнения любого действия результат должен размещаться в разрядной сетке относительно зафиксированного положения запятой. Длина разрядной сетки всегда фиксирована, поэтому разрядность целой части изначально должна быть выбрана такой, чтобы вмещать любое возможное по величине значение. Из-за фиксированной длины разрядной сетки приходится всегда ограничивать в получившемся результате и количество разрядов после запятой. Фактически это означает округление результатов вычислений и может приводить к накоплению погрешностей проведения вычислений.
Числа с плавающей запятой. Форма с плавающей запятой предусматривает представление числа в показательной форме. Например, десятичное число 685,73 представляется в форме 0,68573 *10 3, здесь 0,68573 – мантисса, 10 – основание десятичной системы счисления, 3 – порядок. Двоичное число 0,000101101, представляется в виде 0,101101 * 2 -11; здесь 0,101101B – мантисса, 2 – основание двоичной системы счисления, – 11B – порядок.
В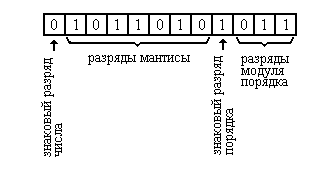
ячейке памяти такие числа хранятся в виде двух групп цифр: первая группа, называемая мантиссой, определяет само число, вторая группа, называемая порядком, – место запятой в числе. Приведенное выше двоичное число может иметь следующее размещение в элементах запоминающей ячейки:
Соответствующим выбором значения порядка можно добиться, чтобы старший разряд мантиссы не был равен нулю. При этом образуется так называемая нормальная форма.
Определим диапазон двоичных чисел, которые могут быть представлены в ячейке памяти в нормальной форме. Обозначим k – число разрядов, отведенных в ячейке для хранения абсолютного значения порядка. Положительное число в ячейке будет иметь наименьшее значение, если минимальное значение будет иметь мантисса (все ее разряды, кроме старшего, будут содержать нуль: 0,100...0B), а порядок будет иметь отрицательный знак и максимальное абсолютное значение (т. е. все разряды модуля порядка будут содержать единицу: 11...1B = 2 k – 1). Таким образом, значение минимального положительного числа в нормальной форме
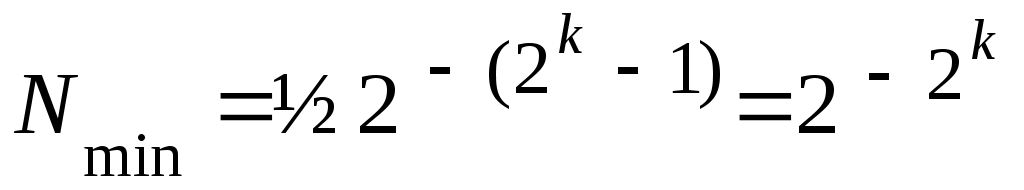 . .
Максимальное число в ячейке образуется при максимальном значении мантиссы (когда мантисса содержит во всех разрядах единицу: 0,11 ...1B = 1) и положительном порядке, имеющем максимальное значение (т. е. если все разряды порядка содержат единицу: 11 ...1B =2 k – 1). Следовательно, максимальное значение числа
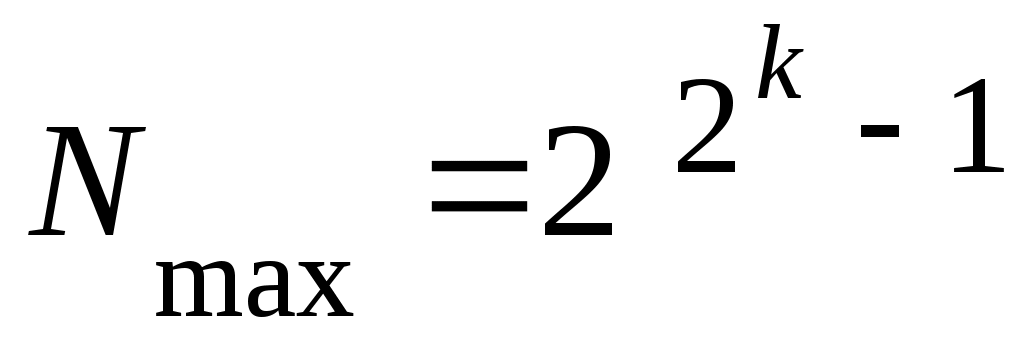 . .
|
 Скачать 0.74 Mb.
Скачать 0.74 Mb.


