Правила нахождения производной суммы, разности, произведения, частного двух функций. Формулы таблицы производных. Производная сложной функции
 Скачать 59.85 Kb. Скачать 59.85 Kb.
|
|
Вопросы к коллоквиуму (НГС, ТНГ, НБС) Определение производной функции в точке. Геометрический и механический смысл производной. Уравнение касательной и нормали к графику функции в данной точке. Правила нахождения производной суммы, разности, произведения, частного двух функций. Формулы таблицы производных. Производная сложной функции. Формула для дифференцирования функции, заданной в параметрическом виде. Дифференцирование функции, заданной в неявном виде. Теорема о производной обратной функции. Обратные тригонометрические функции и их дифференцирование. Определение второй производной функции. Механический смысл второй производной от функции, описывающей прямолинейное движение материальной точки. Определение приращения функции и приращения аргумента. Определение дифференциала функции. Понятие дифференциала независимой переменной. Геометрический смысл дифференциала функции. Правило нахождения дифференциала суммы, разности, произведения, частного двух функций. Применение дифференциала к приближенным вычислениям. Оценка погрешности приближенных вычислений. Дифференциал второго порядка. Дифференциалы 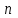 -го порядка. -го порядка.Понятие производной 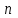 -го порядка. -го порядка.Определение непрерывности функции в точке. Связь непрерывности и дифференцируемости функции в точке и на интервале. Определение точки возврата функции (или точки острого экстремума). Определение угловой точки функции. Теорема Ферма. Геометрический смысл теоремы Ферма. Теорема Ролля. Геометрический смысл теоремы Ролля. Теорема Коши. Формула конечных приращений (формула Лагранжа). Геометрический смысл теоремы Лагранжа. Правило Лопиталя. Применение правила Лопиталя. Необходимое и достаточное условия постоянства функции на некотором промежутке. Определение возрастающей (убывающей) функции. Достаточное условие возрастания функции. Достаточное условие убывания функции. Определение точки максимума функции. Определение точки минимума функции. Определение точки экстремума функции. Определение критической точки. Необходимое условие экстремума функции. Достаточное условие экстремума, использующее производную 1-го порядка. Достаточное условие экстремума, использующее производную 2-го порядка. Понятие гладкой функции и гладкого экстремума. Понятие острого экстремума функции. Понятие наибольшего и наименьшего значений функции на промежутке. Определение графика функции у = f(x), выпуклого вверх (или Определение выпуклого графика функции у = f(x)). Определение графика функции у = f(x), выпуклого вниз(или Определение вогнутого графика функции у = f(x)). Достаточное условие выпуклости (вогнутости) графика функции. Определение точки перегиба графика функции. Достаточное условие существования точки перегиба графика функции. Определение асимптоты графика функции. Вертикальные асимптоты графика функции. Наклонные асимптоты графика функции. Горизонтальные асимптоты графика функции. Формулы для нахождения коэффициентов 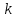 и и 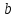 в уравнении наклонной асимптоты в уравнении наклонной асимптоты 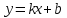 . .Неопределённый интеграл: определение, свойства. Интегрирование по частям. Интегрирование рациональных дробей: теорема о разложении правильной дроби на простейшие. Классификация простейших дробей. Интегрирование простейших дробей. Понятие комплексного числа. Сопряжённое комплексное число. Модуль, аргумент комплексного числа. Различные формы записи комплексного числа. Равенство комплексных чисел. Сумма, разность 2-х комплексных чисел Произведение 2-х комплексных чисел Частное 2-х комплексных чисел Формула Муавра. Формула Эйлера. |
