тфкп вычеты. Правило разложения в ряды Тейлора и Лорана
 Скачать 237.97 Kb. Скачать 237.97 Kb.
|
|
Правило разложения в ряды Тейлора и Лорана. Пусть задана регулярная функция f(z), требуется найти все ее разложения по степеням (z-a). Вначале надо определить все особые точки данной функции. Затем на чертеже отметить точку z = a и все особые точки данной функции. Далее надо построить концентрические окружности с центром в точке z = a, на которых лежат особые точки. Эти окружности разобьют всю плоскость на ряд областей: первая область – круг, окружность которого проходит через ближайшую особую точку функции f(z); последняя – внешняя область будет вся часть плоскости, лежащая вне окружности, проходящей через наиболее удаленную от точки z = a особую точку функции f(z). В каждой из этих областей регулярная функция имеет свое разложение по степеням (z-a). Нули и изолированные особые точки. Пусть f(z) регулярна в точке z = a. Тогда в некоторой окрестности этой точки f(z) представима рядом Тейлора 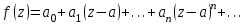 Определение 1. Точка a называется нулем функции f(z) порядка (кратности) “m”, если в окрестности этой точки разложение функции в ряд Тейлора имеет вид 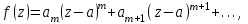 где am ≠ 0 (1) где am ≠ 0 (1)Определение 2(равносильное). Точка a называется нулем функции f(z) порядка (кратности) “m”, если выполняются условия 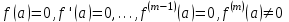 . .Из (1) вытекаетОпределение 3 (равносильное). Точка a называется нулем функции f(z) порядка (кратности) “m”, если в некоторой окрестности этой точки имеет место равенство 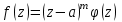 , ,где φ(z) регулярна в точке a и φ(z) ≠ 0. Пусть теперь точка z = a является особой для регулярной функции f(z). Определение 4. Точка a называется изолированной особой точкой функции f(z), если f(z) регулярна в некоторой окрестности этой точки, за исключением самой точки a, т.е. в некоторой окрестности точки aнет других особых точек функции f(z), кроме самой точки a. Если z = a изолированная особая точка, то в некотором кольце с центром в точке z=a функция f(z) разлагается в ряд Лорана 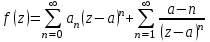 (2) (2)При этом могут быть три случая. 1 СЛУЧАЙ.Главная часть разложения отсутствует. Тогда имеем 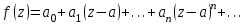 , причем ряд сходится к функции f(z) во всех точках рассматриваемой окрестности, кроме точки z = a, а в этой точке он сходится к числу a0. Функция же f(z) в точке z = a не определена. , причем ряд сходится к функции f(z) во всех точках рассматриваемой окрестности, кроме точки z = a, а в этой точке он сходится к числу a0. Функция же f(z) в точке z = a не определена.Определение 5. Особая точка a называется устранимой особой точкой функции f(z), если разложение f(z) в ряд Лорана по степеням (z-a) не содержит главной части. Определение 6 (равносильное). Особая точка a называется устранимой особой точкой функции f(z), если существует конечный предел функции f(z) в точке a. Пример. 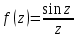 . И другие функции вида . И другие функции вида 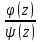 , у которых φ(z) и ψ(z) имеют в одной точке нуль одинаковой кратности. , у которых φ(z) и ψ(z) имеют в одной точке нуль одинаковой кратности.Слово “устранимая” проистекает из-за того, что если доопределить f(z) в точке z = a значением a0, то получим функцию регулярную во всей окрестности. 2 СЛУЧАЙ. Главная часть разложения имеет конечное число членов. Тогда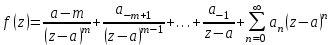 причем a-m≠ 0 (3) причем a-m≠ 0 (3)Определение 7. Точка z = a называется полюсом порядка (или крайности) mфункции f(z), если главная часть разложения функции f(z) в ряд Лорана по степеням (z-a) содержит m членов. В равенстве (3) вынесем за скобку 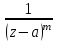 . Получим . Получим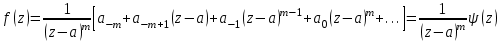 , ,где 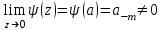 . .Определение 8 (равносильное). Точка z = a называется полюсом порядка (или крайности) m функции f(z), если в некоторой окрестности этой точки имеет место равенство 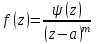 , ,где ψ(z) регулярна в точке a и ψ(а) ≠ 0. Сопоставляя определения 3 и 8 получимТеорему. Если точка a есть нуль порядка m для функции f(z) (или полюс порядка m) то та же точка для функции 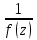 будет полюсом порядка m (соответственно нулем порядка m). будет полюсом порядка m (соответственно нулем порядка m).Из определения 8 так же вытекает Определение 9 Особая точка a называется полюсом функции f(z), если 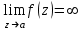 . .Определение 10. В случае m = 1 полюс называется простым. 3 СЛУЧАЙ. Главная часть разложения имеет бесконечное число членов. Определение 11. Точка z = a называется существенно особой точкой функции f(z), если главная часть разложения функции f(z) в ряд Лорана по степеням (z-a) содержит бесконечное число членов. Тогда в точке a функция f(z) не имеет предела ни конечного, ни бесконечного, и для любого числа А можно найти такую последовательность 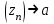 , что , что 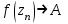 . (Теорема Сохотского). . (Теорема Сохотского).Пример: 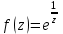 , z = 0 является существенно особой точкой, т.к. , z = 0 является существенно особой точкой, т.к. 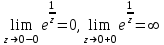 или или 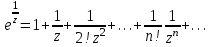 Замечание 1. Не надо думать, что особые точки регулярной функции обязательно изолированные. Так, для 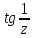 точка z = 0 является существенно особой. Но эта точка не изолированная. Действительно, точки точка z = 0 является существенно особой. Но эта точка не изолированная. Действительно, точки 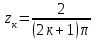 , где к=0, ±1, ±2, являются полюсами функции , где к=0, ±1, ±2, являются полюсами функции 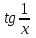 , и при достаточно большом , и при достаточно большом 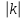 они будут находиться в окрестности точки z = 0, как бы мала она ни была. они будут находиться в окрестности точки z = 0, как бы мала она ни была.Замечание 2. Поведение функции f(z) в окрестности бесконечно удаленной точки (т.е. при 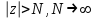 ) можно охарактеризовать через поведение функции ) можно охарактеризовать через поведение функции 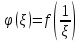 в точке ξ = 0. Это значит, для в точке ξ = 0. Это значит, для 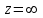 части ряда Лорана меняют свое значение. части ряда Лорана меняют свое значение.Ряд по положительным степеням z будет главной частью, а ряд по отрицательным степеням z – регулярной частью. Соответственно изменятся все определения. Т.е., например, f(z) имеет нуль порядка m в ∞, если она представлена в виде 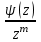 , f(z) имеет полюс порядка m в ∞, если , f(z) имеет полюс порядка m в ∞, если 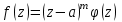 . .Аналогично изменяются все остальные определения. Вычеты Определение 1. вычетом функции 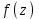 в ее изолированной особой точке а называется число, обозначаемое символом в ее изолированной особой точке а называется число, обозначаемое символом 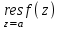 и и 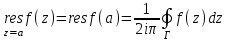 (1) где Г – замкнутый контур, окружающий единственную особую точку z = a и интегрирование по Г совершается в положительном направлении. (1) где Г – замкнутый контур, окружающий единственную особую точку z = a и интегрирование по Г совершается в положительном направлении.Из формул, по которым определяются коэффициенты ряда Лорана, вытекает следующее утверждение. Лемма. Вычет функции 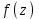 в особой точке z = aравен коэффициенту в особой точке z = aравен коэффициенту 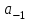 при члене при члене 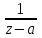 в разложении функции в ряд Лорана в окрестности точки z = a , т.е. в разложении функции в ряд Лорана в окрестности точки z = a , т.е. 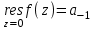 . .Определение 2. Вычетом функции 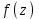 в бесконечно удаленной точке называется коэффициент разложения при в бесконечно удаленной точке называется коэффициент разложения при 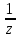 , взять с обратным знаком, т.е. , взять с обратным знаком, т.е. 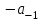 . . Замечание. В окрестности бесконечно удаленной точки член 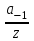 принадлежит не главной, а регулярной части. принадлежит не главной, а регулярной части.Основная теорема о вычетах. Если функция 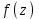 регулярна в замкнутой области регулярна в замкнутой области 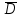 , ограниченной контуром Г, за исключением конечного числа точек z1, z2, …, zn, лежащих в D и являющихся полюсами или существенно особыми точками , ограниченной контуром Г, за исключением конечного числа точек z1, z2, …, zn, лежащих в D и являющихся полюсами или существенно особыми точками 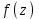 , то справедлива формула , то справедлива формула 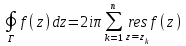 . .Д о к а з а т е л ь с т в о. Окружим точки zk , k=1, …,n замкнутыми контурами 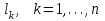 , так, чтобы эти контуры лежали внутри Г, взаимно не пересекались и чтобы внутри каждого контура находилась только одна особая точка. Все это возможно, , так, чтобы эти контуры лежали внутри Г, взаимно не пересекались и чтобы внутри каждого контура находилась только одна особая точка. Все это возможно, 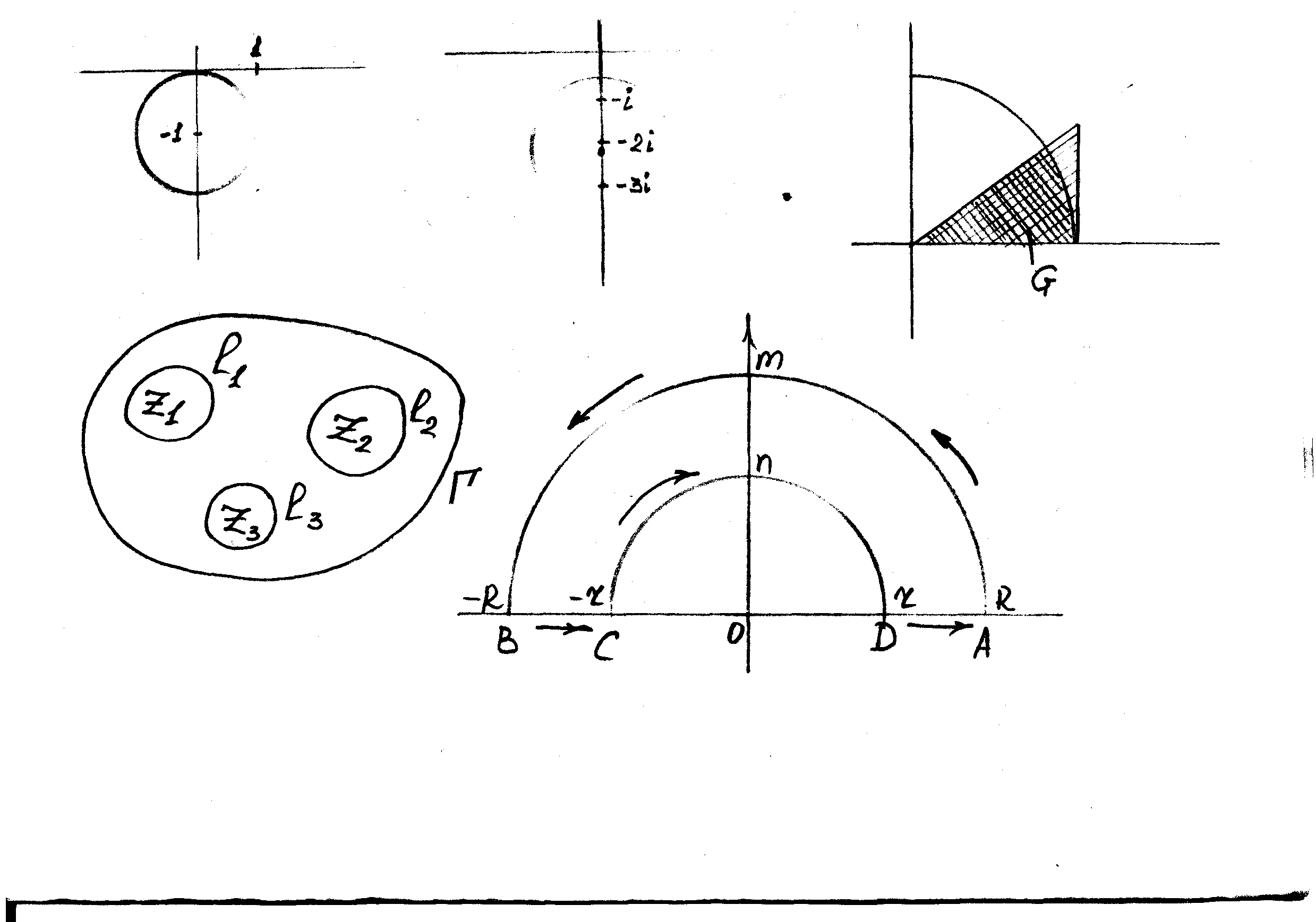 т.к. zk – изолированные особые точки. Тогда образуется многосвязная область, ограниченная внешним контуром Г и внутренними контурами 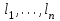 . Функция . Функция 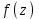 регулярна в этой области и ее границе. Поэтому по теореме Коши для многосвязной области можем написать регулярна в этой области и ее границе. Поэтому по теореме Коши для многосвязной области можем написать 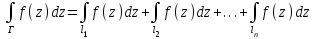 . Отсюда, обозначая вычеты в точках z1, z2, …, zп соответственночерез . Отсюда, обозначая вычеты в точках z1, z2, …, zп соответственночерез 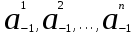 и пользуясь равенством (1), получим и пользуясь равенством (1), получим 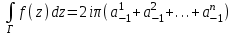 , что и т. д. , что и т. д.Лемма 1. Вычет в устранимой особой точке равен нулю. Д о к а з а т е л ь с т в о. 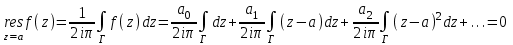 Лемма 2. Если z = a есть полюс первого порядка функции 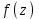 . Тогда . Тогда 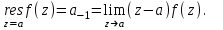 Д о к а з а т е л ь с т в о. Если z = a есть полюс первого порядка функции 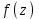 , то , то 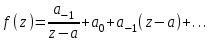 Умножим обе части этого равенства на z – a и перейдем к пределу при 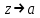 . Получим требуемое равенство. . Получим требуемое равенство.Лемма 3. Если 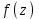 в окрестности точки а может быть представлена как отношение регулярных функций в окрестности точки а может быть представлена как отношение регулярных функций 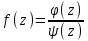 причем причем 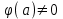 , , 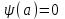 , , 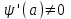 , точка а – простой полюс, то , точка а – простой полюс, то 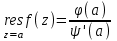 . .Д о к а з а т е л ь с т в о. 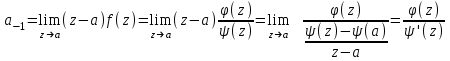 . .Лемма 4. Если z = a есть полюс порядка m функции 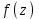 , то , то 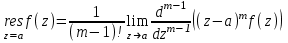 . .Д о к а з а т е л ь с т в о. Если z = a есть полюс порядка m функции 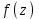 , то , то 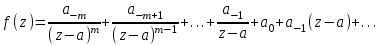 Умножим обе части этого равенства на (z – a)m 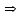 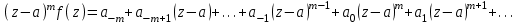 Продифференцировав этот ряд m – 1 раз, получим Продифференцировав этот ряд m – 1 раз, получим 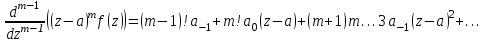 Переходя к пределу Переходя к пределу 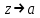 , получим требуемую формулу. , получим требуемую формулу.Практическое занятие Пример__6'>Пример_5'>Пример 1. Для функции 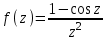 особой точкой является особой точкой является 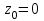 . Покажем это. . Покажем это.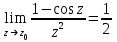 ; ;значит 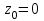 есть устранимая особая точка. есть устранимая особая точка.Пример 2. Для функции 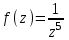 , , 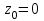 является особой точкой. Так как является особой точкой. Так как 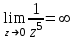 , , 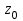 – это полюс. Так как для функции – это полюс. Так как для функции 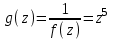 точка точка 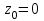 является нулем пятого порядка для функции является нулем пятого порядка для функции 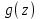 , то , то 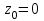 – полюс пятого порядка функции – полюс пятого порядка функции 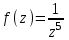 . .Пример 3. Для функции 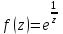 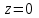 является особой точкой. Разложение является особой точкой. Разложение 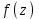 в ряд Лорана: в ряд Лорана: 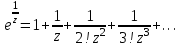 в главной части содержит бесконечное число членов; это существенно особая точка. в главной части содержит бесконечное число членов; это существенно особая точка.Пример 4. Найти все особые точки функции 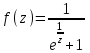 и определить их тип. и определить их тип.Особыми точками являются точка 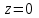 и точки, в которых знаменатель обращается в нуль. Имеем и точки, в которых знаменатель обращается в нуль. Имеем 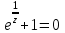 , откуда , откуда 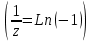 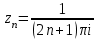 , причем эти точки являются нулями первого порядка. Следовательно, в точках , причем эти точки являются нулями первого порядка. Следовательно, в точках 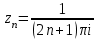 , , 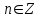 функция функция 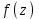 имеет простые полюса. Точка имеет простые полюса. Точка 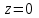 не является изолированной особой точкой, так как она является пределом полюсов: не является изолированной особой точкой, так как она является пределом полюсов: 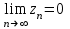 , это означает, что любая окрестность точки , это означает, что любая окрестность точки 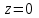 содержит бесконечное число особых точек содержит бесконечное число особых точек 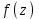 . .Пример 5. Найти все особые точки функции 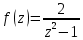 и указать их тип. и указать их тип.Решение. Функция имеет три изолированные особые точки 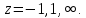 Так как для Так как для
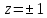 – простые нули, то согласно теореме 4.7.1 точки – простые нули, то согласно теореме 4.7.1 точки 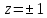 – простые полюса для – простые полюса для 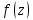 . Поскольку . Поскольку
то 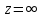 – устранимая особая точка. – устранимая особая точка. Пример 6. Найти все особые точки функции 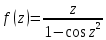 и указать их тип. и указать их тип.Решение. Особые точки функции 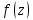 располагаются в нулях знаменателя располагаются в нулях знаменателя 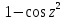 и бесконечно удаленной точке и бесконечно удаленной точке 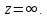 Нулями знаменателя являются точки Нулями знаменателя являются точки 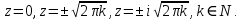 В окрестности 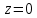 имеем имеем
Следовательно, 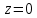 – полюс третьего порядка. – полюс третьего порядка. В окрестности точек 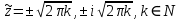 , раскладывать функцию , раскладывать функцию 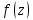 в ряд Тейлора неудобно. Вычислим несколько первых производных в ряд Тейлора неудобно. Вычислим несколько первых производных
Таким образом, 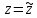 – ноль второго порядка для знаменателя. Поскольку числитель функции – ноль второго порядка для знаменателя. Поскольку числитель функции 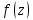 не обращается в ноль в точках не обращается в ноль в точках 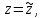 то то 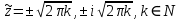 , – полюса второго порядка. , – полюса второго порядка. Так как точки 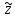 накапливаются на бесконечности, то накапливаются на бесконечности, то 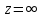 не является изолированной особой точкой. ■ не является изолированной особой точкой. ■Пример 7. Найти все особые точки функции 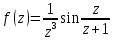 и указать их тип. и указать их тип.Решение. Функция имеет три изолированные особые точки 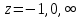 . Поскольку не существует предела . Поскольку не существует предела 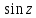 при при 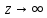 , то и не существует предела , то и не существует предела 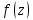 при при 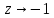 , следовательно, , следовательно, 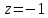 – существенно особая точка. – существенно особая точка. Точка 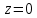 является нулем первого порядка. Действительно, является нулем первого порядка. Действительно,
Поскольку для 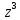 точка точка 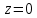 – ноль третьего порядка, то – ноль третьего порядка, то 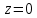 – полюс второго порядка для – полюс второго порядка для 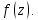 Так как
то 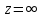 – устранимая особая точка.■ – устранимая особая точка.■Упражнения для самостоятельной работы Определить порядок нуля функции в точке 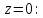
Ответы: 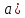 ноль второго порядка, b) ноль четвертого порядка. ноль второго порядка, b) ноль четвертого порядка.Определить тип особенности в точке 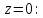
Ответы: 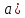 полюс 10 порядка, b) полюс 12 порядка. полюс 10 порядка, b) полюс 12 порядка.Найти все особые точки и указать их тип:
Ответы:a) 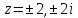 – полюса первого порядка, – полюса первого порядка, 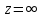 – устранимая особая точка; c) – устранимая особая точка; c) 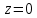 – полюс второго порядка, – полюс второго порядка, 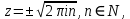 – полюса первого порядка, – полюса первого порядка, 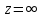 – существенно особая точка; – существенно особая точка; Пример 8. Найти вычеты функции 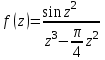 в ее особых точках. в ее особых точках.Особыми точками 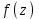 являются точки являются точки 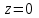 и и 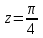 . .В точке 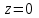 найдем: найдем: 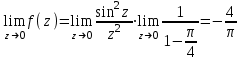 , т.е. точка , т.е. точка 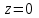 – устранимая особая точка функции – устранимая особая точка функции 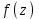 . Поэтому . Поэтому 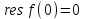 , в точке , в точке 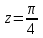 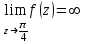 , т.е. точка , т.е. точка 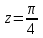 - полюс (первого порядка) функции. По формуле (73) имеем - полюс (первого порядка) функции. По формуле (73) имеем 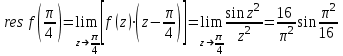 . .Пример 9. Определить вычет функции 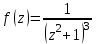 относительно точки относительно точки 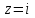 . .Точка 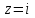 является полюсом третьего порядка функции, т.к. является полюсом третьего порядка функции, т.к. 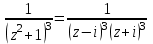 . В соответствии с (75) получим: . В соответствии с (75) получим: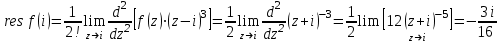 . .Пример 10. Найти вычет функции 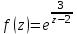 в ее особых точках. в ее особых точках.Особой для данной функции является точка 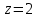 . Это – существенно особая точка (из свойств функции . Это – существенно особая точка (из свойств функции 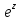 следует, что существует следует, что существует 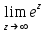 ). Для определения вычета найдем коэффициент ). Для определения вычета найдем коэффициент 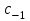 разложения функции разложения функции 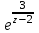 в ряд Лорана по степеням в ряд Лорана по степеням 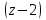 . Так как . Так как 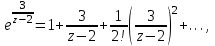 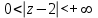 , следовательно , следовательно 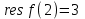 . .Пример11. Вычислить вычеты в простых и кратных полюсах функций: 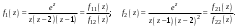 Решение. Полюса функции 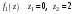 и и 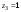 являются простыми. Поэтому являются простыми. Поэтому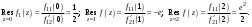 Полюса функции 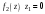 и и 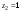 являются простыми, а полюс являются простыми, а полюс 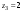 – второй кратности. Поэтому – второй кратности. Поэтому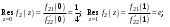 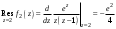 . . Задачи для самостоятельного решения Для следующих функций найти вычеты относительно ее конечных изолированных особых точек: а) 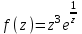 ; б) ; б) 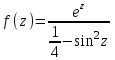 ; в) ; в) 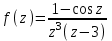 ; ; |

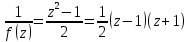
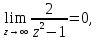
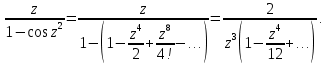
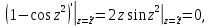
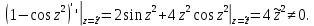
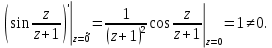
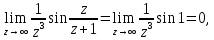
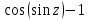 ,
,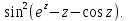
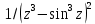 ,
,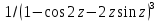 .
.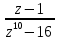 ;
;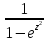 ;
;