Этап урока
(название, время, цели)
|
Деятельность
учителя
|
Задания для учащихся, выполнение которых приведёт к достижению запланированных результатов
|
Деятельность
учеников
|
1. Мотивационно-целевой этап
|
|
|
|
Актуализация знаний.
4 минуты
|
Предлагает ответить на вопросы.
Устная работа по файлу «Начало урока», слайды 1 потом 11, 2 потом 12, 3-13, 4-14, 5-15, 6-16, 7-17.
|
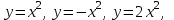
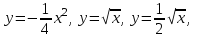 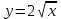
Назвать график и функцию, если есть.
Назвать аналитическую формулу.
Назовите преобразование графика, если оно есть.
Назовите координаты вершины параболы.
|
Устно называют функции и графики, которые им известны; есть ли какое-нибудь изменение базового графика, если есть назовите коэффициент(фронтальная работа)
|
Проблематизация.
2 минут
|
1)Предлагает слайды 9 и 10 в файле «Начало урока»
2)Организует диалог с учащимися.
|
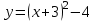 ; ;
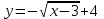 . .
1) Можете ли вы назвать график? (ДА)
Аналитическую формулу? (НЕТ)
Какое преобразование выполнены? (Смещены, сдвинуты)
Можете вы сказать, как сдвиг повлиял на аналитическую формулу функции? (НЕТ)
2)А может быть существует другой способ решения? Предлагайте!
|
1) Устно отвечают на вопросы учителя.
Определяют, что два последних слайда не могут назвать аналитическую формулу функции.
2)Предлагают версии решениязадачи по нахождению формулы;
озвучивают, что формулу не выяснить ранее известными способами.
|
Целеполагание.
2 минуты
|
Предлагает сформулировать цель и задачи урока.
|
Как Вы думаете, чем мы будем заниматься на уроке?
Какова наша задача?
|
Формулируют цели урока и задачи урока.
|
2. Процессуальный этап
Решение учебной задачи (проблемной задачи)
|
|
|
|
2.1. Этап моделирования.
15 минут
|
1)Предлагает работу с раздаточным материалом.
Задание №1: 4 варианта заданий.
2)Все пары закончили работу. Сверяем полученные графики с шаблоном в Файле «Эталон и правило»
3) Организует диалог с учащимися.
4) Предлагает выяснить закономерность коэффициентов в формуле функции со смещением графика вдоль оси ОУ.
5)Предлагает работу с раздаточным материалом. Задание №2, 4 варианта графиков
6)Работа закончена. Сверяем полученные графики с шаблоном в Файле «Эталон и правило»
7) Организует диалог с учащимися.
8) Предлагает выяснить закономерность коэффициентов в формуле функции со смещением графика вдоль оси ОХ.
|
1) Работаем в парах (соседи по парте).
Договоритесь, кто из вас будет заполнять таблицу координат точек графика, другой ученик строит график на готовом шаблоне системы координат
2)На экране появляются последовательно графики, слайды 1В1, 1В2, 1В3, 1В4, ученики сверяют свои работы.
3) Вопросы в шаблоне: Как называется график? Какие изменения в базовом графике можно заметить?
4) Файл «Бегунок»
Слайды b1,b2, замечаем смещение.
Как изменялись координаты каждой точки графика?
Слайды т1,т2.
5) Работаем в парах (соседи по парте).
Поменяйтесь работой, кто из вас будет заполнять таблицу координат точек графика, другой ученик строит график на готовом шаблоне системы координат
6)На экране появляются последовательно графики, слайды 2В1, 2В2, 2В3, 2В4, ученики сверяют свои работы.
7) Вопросы в шаблоне: Как называется график? Какие изменения в базовом графике можно заметить?
8) Файл «Бегунок»
Слайды а1,а2, замечаем смещение.
Как изменялись координаты каждой точки графика?
Слайды т3,т4.
|
1)Каждая пара работает с шаблоном функции и выполняет задание: заполнить таблицу, построить два графика фломастером. И письменно отвечают на вопросы в шаблоне.
2) Каждая пара поднимает и показывает свои графики и сверяет их с графиками на доске.
3)Каждая пара озвучивает свои ответы на вопросы в шаблоне.
4) Устно по слайдам проговаривают закономерности и формулируют правило смещения графика вдоль ОУ и изменения координат каждой точки графика.
5)Каждая пара работает с шаблоном функции и выполняет задание: заполнить таблицу, построить два графика фломастером. И письменно отвечают на вопросы в шаблоне.
6) Каждая пара поднимает и показывает свои графики и сверяет их с графиками на доске.
7)Каждая пара озвучивает свои ответы на вопросы в шаблоне.
8) Устно по слайдам проговаривают закономерности и формулируют правило смещения графика вдоль ОХ и изменения координат каждой точки графика.
|
2.2. Этап конструирования.
10 минут
|
1)Предлагает сделать вывод о полученных закономерностях и заполнить шаблон правила смещения вдоль ОХ и смещения вдоль ОУ.
2) Файл «Эталон и правило», предлагает сверить свои шаблоны правил с эталоном с проговариванием вслух.
|
1)Какие закономерности мы получили?
На партах шаблон Правило 1 и Правило 2.
2) Файл «Эталон и правило», слайды пр1, пр12, пр2, пр22.
|
1)Заполняют шаблоны праило1 и правило2.
2)Сверяют свои шаблоны с правилом на доске и проговаривают вслух эти правила
|
2.3. Этап реализации
8 минут
|
1)Предлагает самостоятельную работу для закрепления, 2 варианта на парте.
2)Предлагает взаимопроверку в парах.
3)Предлагает сверить результаты работы с ответами на доске.
4)Организует обсуждение трудностей в процессе выполнения самостоятельной работы.
5)Задает домашнее задание:
Параграф 10, №308, 309, 311, 313.
|
1)Выполните самостоятельную работу по вариантам. Время выполнения 4 минуты.
2) Поменяйтесь тетрадями в парах и проверьте работу соседа.Каждое правильно выполненное задание оценивается в один балл.
3)На доске ответы самостоятельной работы.
4)Проверяем полученный результат. Какие ошибки допущены? Какие трудности возникли?
5)Запишите домашнее задание.
|
1) Выполняют задания самостоятельной работы по вариантам.
2) Проверяют работу соседа, выставляют оценку, озвучивают результаты.
3)Сверяют, озвучивают результаты.
4)Отвечают на вопросы учителя по работе.
5) Записывают домашнее задание
|
3. Рефлексивно-оценочный этап.
Рефлексия деятельности.
4 минуты
|
1)Предлагает вернуться к заданиям которые класс не смог выполнить в начале урока.
Слайды 9 и 10 в файле «Начало урока»
2)Предлагает рефлексию.
|
1)Давайте посмотрим графики функций и назовем аналитические формулы функции:
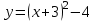 ; ;
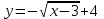 . .
2)Давайте вместе ответим на вопросы, которые помогут нам оценить работу, которую мы проделали и подвести итоги:
1) Как вы понимаете выражение «преобразование базового графика»?
2) Что еще изменяется, кроме графика при выполнении преобразования?
3) С какими видами преобразования вы знакомы?
4) Достигли ли мы планируемой цели?
5) Смогли ли мы решить поставленные задачи?
|
1)Называют формулы смещенных графиков.
2)Озвучивают ответы на вопросы.
|
 Скачать 48.57 Kb.
Скачать 48.57 Kb.