переменный ток 5гр. Преобразование переменного тока в постоянный
 Скачать 1.2 Mb.
|
 Преобразование переменного тока в постоянный. Из переменного тока, можно получить постоянный ток, для этого достаточно подключить сети переменного тока диодный мост или как его еще называют “выпрямитель”. Из названия “выпрямитель” как нельзя лучше понятно, что делает диодный мост, он выпрямляет синусоиду переменного тока в прямую линию тем самым заставляя двигаться электроны в одном направлении. 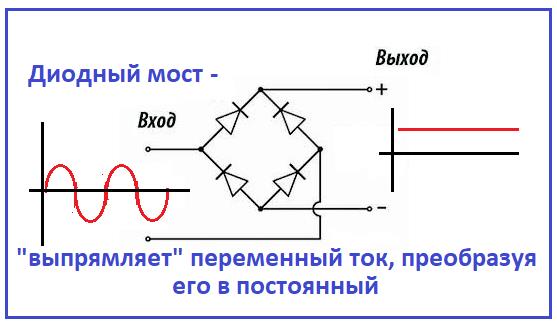  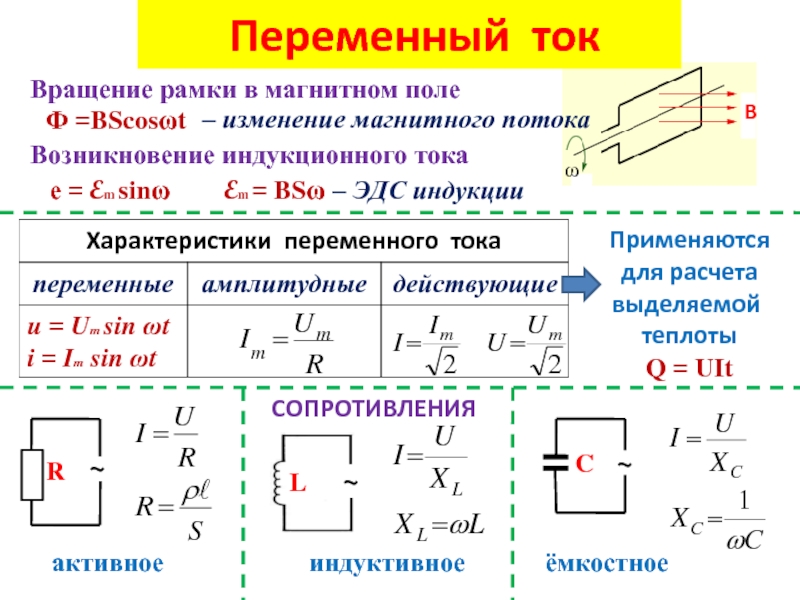   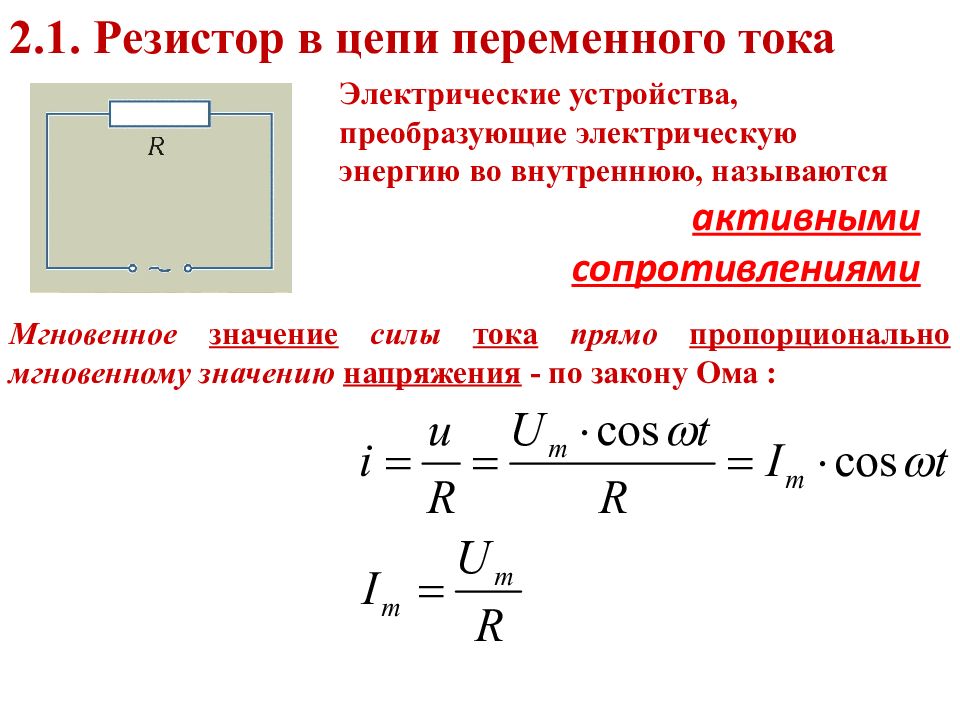 Колебания силы тока в цепи резистора совпадают по фазе с колебаниями напряжения.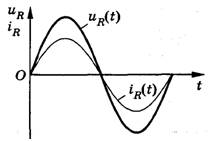  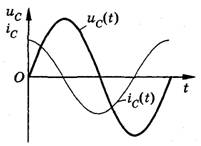  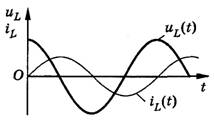  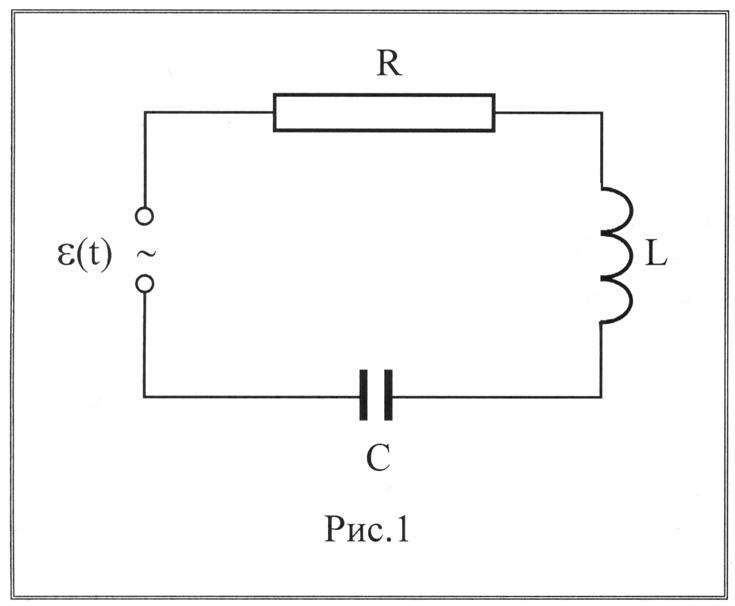  Рассмотрим примеры решения задач: Примеры решения расчетных задач Задача 1. Определите сдвиг фаз колебаний напряжения  и силы тока  для электрической цепи, состоящей из последовательно включенных проводников с активным сопротивлением R = 1000 Ом, катушки индуктивностью L = 0,5 Гн и конденсатора емкостью С = 1 мкФ. Определите мощность, которая выделяется в цепи, если амплитуда напряжения U0 = 100 В, а частота  = 50 Гц.Решение: Сдвиг фаз между током и напряжением в цепях переменного тока определяется соотношением 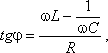 (1)здесь  = 2 - циклическая частота. Следовательно, Мощность, которая выделяется в цепи, определится по формуле  Для цепи переменного тока справедливо соотношение  где Z - полное сопротивление (импеданс) цепи:  Следовательно, мощность, которая выделяется в цепи 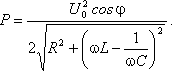 (2)Подставив численные значения в (1), получим  (минус 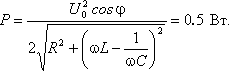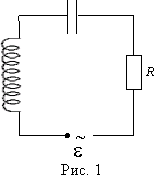означает, что напряжение отстает по фазе). Тогда  . Подставив численные значения в (2), получим P = 0,5 Вт.Ответ:   Задача 2. Конденсатор неизвестной емкости, катушка с индуктивностью L и сопротивлением R подключены к источнику переменного напряжения  (рис. 1). Сила тока в цепи равна  . Определите амплитуду напряжения между обкладками конденсатора.Решение: Из условия задачи видно, что сила тока и напряжение в цепи меняются синфазно. Это означает, что совпадают индуктивное и емкостное сопротивления.  (3)Напряжение на конденсаторе будет равно  (4)Поскольку  , то (5)Подставляя (5) в (4), получим:  (6)С учетом (3) соотношение (6) примет вид:  Поэтому амплитудное значение напряжения между обкладками конденсатора будет равно  Ответ:  Задача 3. В электрической цепи из двух одинаковых конденсаторов емкости С и катушки с индуктивностью L, соединенных последовательно, в начальный момент времени один конденсатор имеет заряд q0, а второй не заряжен (рис. 2). Как будут изменяться со временем заряды конденсаторов и сила тока в контуре после замыкания ключа К? Решение: Цепь, приведенная на рис. 2, представляет собой колебательный контур. Сила тока в нем будет меняться по закону  (7)Чтобы ответить на вопрос задачи, нужно найти максимальное значение силы тока I0 и частоту колебаний . Частоту колебаний можно определить по формуле (8)где Сэкв - емкость системы из двух последовательно соединенных конденсаторов емкостью С:  Подставляя значение Сэкв в (8), получим, что частота колебаний в контуре будет равна  (9)Подставим значение частоты (9) в выражение для силы тока (7), тогда получим, что сила тока в цепи будет меняться по закону  (10)Для определения I0 можно воспользоваться законом сохранения энергии. Пусть в некоторый момент времени заряд одного из конденсаторов равен q1 , тогда заряд второго конденсатора будет q2 = q0 - q1 . В начальный момент времени энергия контура сосредоточена в электрическом поле заряженного конденсатора, в произвольный момент времени она перераспределяется между энергией электрического поля двух заряженных конденсаторов и энергией магнитного поля, сосредоточенного в катушке индуктивности. Следовательно, согласно закону сохранения энергии,  Отсюда можно найти зависимость силы тока от заряда q1.  Чтобы найти максимальное значение силы тока, нужно взять производную от I по q1 и приравнять ее к нулю.  Из последнего выражения видно, что максимальное значение силы тока достигается при  . Следовательно, Подставляя полученное значение для максимального значения силы тока в (10), получим, что сила тока в цепи будет меняться по закону  Чтобы найти закон изменения зарядов на пластинах конденсатора, воспользуемся выражением  . Преобразовав его, получим квадратное уравнение для q1: Решая уравнение, получим:  Разные знаки означают, что в начальный момент времени любой конденсатор может либо иметь заряд q0, либо быть незаряженным. Пусть  Тогда  Ответ:  Задача 4. Имеются два колебательных контура с одинаковыми катушками и конденсаторами. В катушку одного из контуров вставили железный сердечник, увеличивший ее индуктивность в n = 4 раза. Найдите отношение резонансных частот контуров и их энергий, если максимальные заряды на конденсаторах одинаковы. Решение: Резонансные частоты контуров могут быть определены по формуле Томсона:  Отсюда  Ответ: 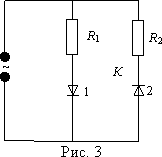  Задача 5. Два сопротивления R1 и R2 и два диода подключены к источнику переменного тока с напряжением U так, как показано на рис. 3. Найдите среднюю мощность, выделяющуюся в цепи. Решение: Ток половину периода идет через один диод (например, 1). За это время на сопротивлении R1 выделяется средняя мощность  В течение второго полупериода ток идет через диод 2, выделяя на нем среднюю мощность  Таким образом, за полный период выделяется средняя мощность  Ответ:  Задачи для самостоятельного решения: № 1. В ц.п.т. с напряжением 220 В включена активная нагрузка сопротивлением 40 Ом. Определите ток цепи. № 2. Определите сопротивление конденсатора емкостью 5 мкФ при частоте 50 Гц. №3. Определите сопротивление катушки индуктивностью 0,01 Гн при частоте 50 Гц. № 4. Определите ток, проходящий через катушку, индуктивное сопротивление которой 5 Ом, а активное сопротивление 1 Ом, если напряжение сети переменного тока 12 В. № 5. В ц.п.т. с напряжением 220 В включена эл.лампа, по спирали которой течет ток 5 А. Вычислите активную мощность этой лампы. № 6. В электрическую цепь напряжением 220 В последовательно включены реостат сопротивлением 5 Ом, катушка с активным сопротивлением 6 Ом и индуктивным сопротивлением 4 Ом, конденсатор с емкостным сопротивлением 3 Ом. Определите ток в цепи. Постройте векторную диаграмму токов и напряжений. № 7. В ц.п.т. с напряжением 220 В включены конденсатор емкостью 100 мкФ и катушка индуктивностью 0,05 Гн. Определите реактивную мощность цепи. Постройте векторную диаграмму токов и напряжений. № 8. В ц.п.т. с напряжением 380 В включены активное сопротивление 50 Ом и конденсатор емкостью 1000 мкФ. Определите полную мощность цепи. Постройте векторную диаграмму токов, напряжений и мощностей. № 9. В ц.п.т. напряжением 110 В последовательно включены активное сопротивление 30 Ом, емкостное – 45 Ом и индуктивное - 50 Ом. Определите полное сопротивление этой цепи. № 10. В ц.п.т. с напряжением 220 В включены активное сопротивление 20 Ом, конденсатор емкостью 100 мкФ и катушка индуктивностью 0,05 Гн. Определите полную мощность цепи. Постройте векторную диаграмму токов, напряжений, мощностей. Домашнее задание: 1.Выучить и законспектировать лекцию. 2. Разобрать и записать в тетрадь примеры решения задач, которые приведены в конце лекции. 3. Ответить на вопросы для самоконтроля. 4. Выполнить на оценку задания в тестовой форме:     |