Реферат Математика. Преобразование плоскости. Метод изучения симметрии в начальной школе
 Скачать 1.71 Mb. Скачать 1.71 Mb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых” (ВлГУ) кафедра психологии и педагогики дошкольного и начального образования Реферат на тему «Преобразование плоскости. Метод изучения симметрии в начальной школе». Выполнила студентка гр. ЗНОу-218 Носкова Полина Сергеевна Руководитель: ст. преподаватель каф.ППДНО Болотова Татьяна Владимировна Владимир 2021 г. Содержание Введение……………………………………………………………………….….3 Преобразование плоскости………………………………………………….5Метод изучения симметрии в начальной школе……….………………...... Вывод……………………………………………………………………….… Список литературы………………………………………………………................… Введение В школу ребёнок приходит уже с определёнными знаниями о геометрических фигурах, объектах, среди которых есть и симметричные. Школа должна ему обеспечить развитие познавательных, интеллектуальных и творческих способностей. Дать учащимся начальные геометрические представления, развить логическое мышление и пространственное воображение детей, сформировать умения узнавать геометрические фигуры и их части. В курсе начальной школы, главным является формирование у ребенка практических умений измерения и построения геометрических фигур с помощью циркуля, угольника и линейки. Задания на вычисления различных параметров геометрических фигур (длин отрезков, периметра и площади прямоугольника и квадрата). Неоценимую роль играет изучение алгебраических, геометрических понятий, в том числе и понятия о симметрии. Включение в начальный курс математики темы «Симметрия», использование проектных технологий на уроках и во внеурочное время по формированию понятий о симметрии позволит развить у детей пространственное мышление, расширить знания о геометрических фигурах, подготовить детей к активному и осмысленному восприятию курса геометрии в средней школе. Детям свойственно в этом возрасте усваивать понятия с помощью наглядно-практических методов, игровых, проектных. Эта работа способствует 3 формированию опыта саморазвития и личностной ответственности учащихся, способности к творческой созидательной деятельности. А это и есть те ключевые компетенции, которые определяют современное качество образования России. На основании вышеизложенного можно сделать вывод, что данная тема, у младших школьников является актуальной, а использование для этого проектных технологий соответствует современным требованиям образования. Данная тема рассматривает следующую цель: развитие логического мышления и пространственного воображения детей; формирование умения знать и называть геометрические фигуры, изображать. На основании цели поставлены задачи: развитие пространственного воображения у ребенка, умения наблюдать, сравнивать, обобщать, анализировать и абстрагировать формирование у ребенка практических умений измерения и построения геометрических фигур с помощью циркуля, угольника и линейки Преобразование плоскости. Метод изучения симметрии в начальной школеВ программе начальной школы геометрический материал изучается на протяжении каждого года. Особой темы не выделяется, материал изучается не углубленно, только в качестве знакомства без терминологии. Ученики учатся строить геометрические фигуры, сравнивать их и изображать. Данную тему мы видим в линии учебников УМК «Школа России», «Перспектива», (Дорофеев Г.В, Миракова Т.Н.), Петерсон и др. Современные методические подходы, к изучению геометрического материала отражают изменения, которые произошли в начальной школе и обучении математике. Плоскостные фигуры моделируют форму частей поверхности твердого тела, форму сечений и теней (проекций), алинейные фигуры — форму границ этих поверхностей, сечений и теней. Форму твердого тела можно задать так же определенным расположением точек, «точечной фигурой». Для графического представления формы разработаны специальные правила изображений, правила построения геометрических фигур с использованием определенных наборов чертежных и измерительных инструментов. Для описания границ поверхностей и границ видимости предназначены линии — замкнутые и незамкнутые, прямые и кривые. Соответствующие геометрические фигуры назовем линейными. Обобщением линий служат понятие прямая и кривая. К линейным геометрическим фигурам относятся также: луч, отрезок, ломаная, многоугольники, понимаемые как замкнутые ломаные линии; угол (как два луча, исходящие из одной точки). Важную информацию о форме предмета несет форма теней (проекций), форма срезов, сечений тел плоскостью. Наблюдения за тенями (проекциями), срезами способствуют развитию представлений о форме, развитию пространственного воображения и формированию понятий о геометрических фигурах. Всем известно, как любят дети рисовать. Карандаши, ручки, фломастеры, мелки — любимые «инструменты» детей. Из-под их «пера» выходят линии самой разной формы. Комментируя рисунки, обучая рисованию, взрослые называют формы линий, их расположение относительно друг друга геометрическими терминами. Занятия изобразительной деятельностью оказывают значительное влияние на геометрическое развитие детей. Плоскостные геометрические фигуры и линии используются в психологических тестах при исследовании мышления. Объясняется это тем, что они удобны для сравнения, образования рядов, представляющих закономерности. С помощью геометрических объектов развивают внимание, память. Модели геометрических фигур, их изображения служат счетным материалом, элементами множеств, с помощью которых представляют числа, арифметические действия, отношения между ними. Геометрические фигуры характеризуются величинами, как и моделируемые ими материальные тела. Все геометрические фигуры, кроме точки, обладают ненулевой длиной. Плоскостные фигуры двумерны, объемные фигуры — трехмерны. Плоскостные и объемные фигуры характеризуются площадью, объемные — объемом. Изучение геометрических величин — важнейший источник представлений учащихся о величинах реальных физических тел. Симметрия по программе «Школа России» М.И. Моро и др. (Слайд 2) В программе по математике «Школа России» М.И. Моро и др. прописано, что: Математические знания и представления о числах, величинах, геометрических фигурах лежат в основе формирования общей картины мира и познания законов его развития. Именно эти знания и представления необходимы для целостного восприятия объектов и явлений природы, многочисленных памятников культуры, сокровищ искусства. Обучение младших школьников математике на основе данной программы способствует развитию и совершенствованию основных познавательных процессов (включая воображение и мышление, память и речь). Содержание курса имеет концентрическое строение, отражающее последовательное расширение области чисел. Такая структура позволяет соблюдать необходимую постепенность в нарастании сложности учебного материала, создаёт хорошие условия для углубления формируемых знаний, отработки умений и навыков, для увеличения степени самостоятельности (при освоении новых знаний, проведении обобщений, формулировании выводов), для постоянного совершенствования универсальных учебных действий. Структура содержания определяет такую последовательность изучения учебного материала, которая обеспечивает не только формирование осознанных и прочных, во многих случаях доведённых до автоматизма навыков вычислений, но и доступное для младших школьников обобщение учебного материала, понимание общих принципов и законов, лежащих в основе изучаемых математических фактов, осознание связей между рассматриваемыми явлениями. Сближенное во времени изучение связанных между собой понятий, действий, задач даёт возможность сопоставлять, сравнивать, противопоставлять их в учебном процессе, выявлять сходства и различия в рассматриваемых фактах. В связи с концентрическим строение курса тема «Симметрия » изучается на протяжении всех 4 лет обучения. В 1 классе даются задания на нахождение зеркального отражения фигуры. (слайд 3) ММ1Ч2с59  Во втором классе дается определение симметрии и ось симметрии. Так же дети учатся определять оси симметрии. На данную тему так же даются задания. Слайд 4 ММ2Ч1с.15  В третьем и четвертом классе акцент на данной теме не делается, но задания на повторения предлагаются. Слайды 5-6 ММ3Ч1с.84  ММ4Ч1с.31  1.2 Симметрия по программе Л.Г. Петерсон Слайд 7 В курсе математики Л.Г. Петерсон сохраняется преемственность с традиционной программой по математике, но усиливается геометрическое содержание за счет большого дополнительного материала (особенно в 4-ом классе), что позволяет расширить геометрические представления и знания учащихся, развивать их пространственное воображение, техническое и логическое мышление, конструкторские умения. Определяется конкретное содержание, основными положениями которого являются: • преемственность с традиционным построением курса математики, что обеспечивает числовую грамотность учащихся, умение решать текстовые задачи, знакомство с величинами и их измерением; • усиление геометрического содержания обеспечивает расширение геометрических представлений и знаний учащихся, развивает их пространственное воображение и логическое мышление. В программу входит знакомство с основными линейными, плоскостными и пространственными геометрическими фигурами и их свойствами. Расширение геометрических представлений и знаний используется для формирования у учащихся элементов технического мышления и конструкторских умений; • обеспечивается формирование умений изображать на бумаге в форме чертежа сначала элементарных геометрических фигур, а затем конструируемые объекты или их части; • активизируется творческое мышление, побуждает к поиску нестандартных математических задач. Изложение геометрического материала проводится в наглядно-практическом плане. Работая с геометрическим материалом, дети знакомятся и используют основные свойства изучаемых геометрических фигур. Задания располагаются в порядке усложнения и постепенного обогащения новыми элементами конструкторского характера. Уже в 1 классе начальной школы идет пропедевтическая работа по теме «Симметрия», но без введения данного термина. В подготовительной работе по теме предлагаются задания вида: дорисуй по образцу Особенностью изучения геометрических понятий в программе Л.Г. Петерсон – их раннее введение на основе построенной многоуровневой системы математических понятий. Тема «Преобразование фигур. Симметрия.» в данной программе изучается в 3 классе и ей отводится 4 урока (Уроки 14-17 в соответствии с программой), что соответствует 4 академическим часам. Согласно данной темы программа предусматривает следующие задачи: - сформировать навык построения симметричных точек, отрезков на клетчатой бумаге с помощью специальных инструментов (линейки, угольника, циркуля); - уметь строить фигуры, симметричные относительно прямой; - учить находить и строить линию симметрии в симметричных фигурах. Реализация задач достигается следующим содержанием программы: - симметрия (построение симметричных фигур); - симметричные фигуры (симметрия на клетчатой бумаге). В заданиях, предложенных Л.Г. Петерсон, предусмотрено использование наглядно-практических и объяснительно-иллюстративных методов и приемов. Слайд 8  На уроках учащиеся выполняют практические действия с фигурами на клетчатой бумаге, в процессе которых их представление о преобразовании фигур уточняются. Понятие «преобразование фигур» можно пояснить, как перемещение фигур на плоскости, их перенос. На 14 уроке рассматривается перенос фигур на данное число клеток вверх, вниз, направо и налево (параллельный перенос) приложение. С детьми надо проговорить вывод о том, что при таких преобразованиях каждая точка фигур перемещается в одном и том же направлении на одно и то же расстояние. При этом линии, соединяющие соответствующие точки фигур, параллельны. Направление расстояния, на которое осуществляется перенос, удобно показывать направленным отрезком или вектором. (с. 37. урок 14) Для построения симметричных фигур выбираются опорные точки (концы отрезков, центры окружностей), строятся симметричные к ним точки, а затем по этим точкам воспроизводятся сами фигуры. Выполняя эти задания, дети должны заметить, что точки, лежащие на оси симметрии, при симметрии переходят сами в себя. (7. с. 43. урок 16) слайды 9-10   На уроках 22 – 25 учащиеся знакомятся с некоторыми преобразованиями фигур на плоскости (параллельный перенос, симметрия), закрепляют приемы письменного умножения и деления многозначного числа на однозначное, отрабатывают навыки устных вычислений, повторяют и закрепляют нумерацию, сложение и вычитание многозначных чисел, решение текстовых задач и уравнений, зависимость между компонентами и результатами арифметических действий, расширяют представление о геометрических фигурах. С преобразованием фигур на плоскости учащиеся уже встречались раньше при рассмотрении равенства фигур, в задачах на построение симметричных фигур и др. Однако сам термин «преобразование фигур» не вводился. На данных уроках ученики выполняют практические действия с фигурами на клетчатой бумаге, в процессе которых их представления о преобразовании фигур уточняются. Понятие «преобразование фигур» можно пояснить как перемещение фигур на плоскости, их перенос. На уроке 22 рассматривается перенос фигур на данное число клеток вверх, вниз, направо и налево (параллельный перенос). Проблема урока связана с «открытием» свойств этого преобразования, которые позволят строить изображения фигур при их параллельном переносе, а именно: 1. Все точки фигур перемещаются в одном и том же направлении на одно и то же расстояние. Это означает, что для построения параллельного переноса фигуры можно выбрать «опорные точки», перенести каждую из них в заданном направлении на одно и то же расстояние, а затем восстановить фигуру по полученным точкам. 2. В результате переноса фигур они не деформируются, т. е. получаются равные фигуры. Значит, для построения параллельного переноса фигуры можно переместить по заданному условию одну какую-нибудь точку, а затем, исходя из нее, восстановить и саму данную фигуру. Таким образом, на этапе актуализации знаний требуется восстановить в памяти обучающихся понятие равных фигур: две фигуры равны, если их можно совместить наложением. Задание № 1, стр. 37 можно использовать на этапах постановки проблемы и «открытия» нового знания. В этом задании в результате выявленных свойств учащиеся переносят данную фигуру сначала на 7 клеток вправо, а затем на 3 клетки вниз одним из указанных выше способов. Задания № 2–4, стр. 37 предназначены для этапа первичного закрепления. В № 2 ученики должны выразить в речи выполняемые преобразования. Можно сказать им, что направление и расстояние, на которое осуществляется перенос, удобно показывать направленным отрезком (вектором), и попросить нарисовать направленные отрезки, соответствующие данным преобразованиям. Так, в задании (а) горизонтальный вектор означает, что фигура переносится на 7 клеток вправо, а вертикальный – что она переносится на 4 клетки вниз; в задании (б) горизонтальный вектор показывает, что фигура переносится на 6 клеток влево, а вертикальный – что она переносится на 5 клеток вверх: Слайд 11  В задании № 3, стр. 37 учащиеся должны не просто выполнить преобразования, но и найти результат их последовательного выполнения (композиции): два переноса – сначала на 15 клеток вправо, а потом на 3 клетки влево – можно заменить одним переносом на 12 клеток вправо. В задании № 4, стр. 37 учащиеся встречаются с понятием обратного преобразования. Задание № 5, стр. 37 можно использовать на этапе самостоятельной работы с самопроверкой в классе. Учащиеся строят в тетради произвольный треугольник, переносят его сначала на 6 клеток вправо, потом на 8 клеток вниз и, наконец, на 6 клеток влево. В завершение они устанавливают, что все эти преобразования можно было заменить одним – переносом треугольника на 8 клеток вниз. Наиболее трудное задание № 6, стр. 38. Предыдущие выполнялись с помощью линейки, а для выполнения этого задания нужен циркуль. Ученики вспоминают, как надо чертить окружность с помощью циркуля, а потом переносят круг, ограниченный этой окружностью, сначала на 9 клеток вниз, потом на 7 клеток вправо, а потом на 5 клеток вверх. Обучающихся надо подвести к мысли о том, что все эти преобразования можно заменить одним преобразованием, определяемым направленным отрезком (или вектором) AD. Слайд 12 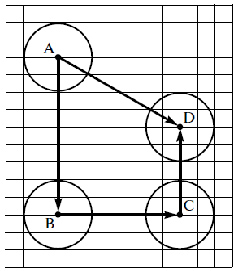 В отличие от традиционной программы, эта тема является дополнительной линией по системе Л.Г. Петерсон. По программе Н.Б. Истоминой Слайд 13 Цель начального курса математики Н.Б.Истоминой - обеспечить предметную подготовку учащихся, достаточную для продолжения математического образования в основной школе, и создать дидактические условия для овладения учащимися универсальными учебными действиями личностными, познавательными, регулятивными, коммуникативными) в процессе усвоения предметного содержания. Достижение основной цели начального образования – формирования у детей умения учиться – требует внедрения в школьную практику новых способов (методов, средств, форм) организации процесса обучения и современных технологий усвоения математического содержания, которые позволяют не только обучать математике, но и воспитывать математикой, не только учить мыслям, но и учить мыслить. В связи с этим в начальном курсе математики реализован целый ряд методических инноваций, связанных с логикой построения содержания курса, с формированием вычислительных навыков, с обучением младших школьников решению задач, с разработкой системы заданий и правил, которые создают дидактические условия для формирования предметных и метапредметных умений в их тесной взаимосвязи. Особенностью курса является логика построения его содержания. Курс математики построен по тематическому принципу. Каждая следующая тема органически связана с предшествующими, что позволяет осуществлять повторение ранее изученных понятий и способов действия в контексте нового содержания. Основным средством формирования универсальных учебных действий в курсе математики являются вариативные по формулировке учебные задания (объясни, проверь, оцени, выбери, сравни, найди закономерность, верно ли утверждение, догадайся, наблюдай, сделай вывод и т.д.), которые нацеливают учащихся на выполнение различных видов деятельности, формируя тем самым умение действовать в соответствии с поставленной целью. Раздел «Геометрические фигуры» содержит материал по теме «Симметрия», который в соответствии с программой, изучается с 1 по 4 класс и определен следующими задачами: 1 класс слайд 14 Познакомить с понятием «симметричные фигуры», «ось симметрии», добиться усвоения данных понятий и учить оперировать ими на практике. Формировать умение отличать симметричные фигуры от несимметричных. МИ1Ч1с40 2 класс Повторение материала, пройденного в 1 классе с целью восстановления в памяти учащихся изученных понятий. Знакомство школьников с геометрическими фигурами (угол, прямоугольник, квадрат, окружность) и их свойствами. 3 класс слайд 15 Познакомить учащихся со способом построения симметричных фигур относительно оси симметрии. Научить выполнять построение геометрических фигур, симметричных данной относительно оси симметрии с помощью линейки, циркуля, угольника. 4 класс Повторение знаний, умений, навыков о геометрических преобразованиях. Построение точки или фигуры, симметричной относительно данной прямой с помощью циркуля и угольника. Реализация задач отражена в содержании программы: - 1 класс. Симметричные фигуры (знакомство с понятием «симметричная фигура»). Доказательство симметричности фигур путём перегибания. Слайд 14 - 3 класс. Симметричные фигуры. Оси симметрии. Построение симметричных фигур относительно данной прямой с помощью линейки, циркуля, угольника. Методы и приемы предусмотренные программой: - Практический метод. - Самостоятельная работа. - Частично-поисковый метод, обсуждения различных способов деятельности. Теме «Симметричные фигуры» в 1-ом классе отводится один час. Теме «Построение симметричных фигур» в 4-ом классе отводиться три часа. Таким образом, мы видим, что на изучение темы «симметрия» в соответствии с программой Н.Б. Истоминой выделено 4 урока, что соответствует 4 академическим часам, но тема выделена к изучению на несколько периодов обучения школьников в начальной школе (1 и 4 класс). Симметрия в программе по математике В.Н. Рудницкой слайд 16 Программа по математике В.Н. Рудницкой разработана в соответствии с требованиями Федерального государственного стандарта начального общего образования к результатам освоения младшими школьниками основ начального курса математики. В ходе исследования мы выяснили, что автор программы В.Н.. Рудницкая предусматривает большой объём геометрического материала по теме «Симметрия», задачами которого являются: слайд 17 - 1 класс: познакомить с симметричными фигурами и осью симметрии; формировать умение показывать пары симметричных точек, предметов или их деталей; умение получать фигуру, симметричную данной, путем перегиба листа бумаги по оси симметрии; проверять перегибанием имеет ли данная фигура ось симметрии. Слайд 18 - 2 класс: повторение и закрепление знаний, умений, навыков по теме «Симметрия». Слайд 19 - 3 класс: научить с помощью линейки, циркуля и угольника строить фигуру, симметричную данной. Слайд 20 - 4 класс: научить строить граф - отношений симметричности; учить определять по графу обладает ли он данным отношением. Содержание раздела геометрии в курсе программы по изучаемой теме распределяется следующим образом: - 1 класс. - Отображение фигур в зеркале. Ось симметрии. Построение симметричных точек, отрезков, многоугольников. Приёмы построения фигуры, симметричной данной фигуре, имеющей 1 или несколько осей симметрии. - 3 класс. - Симметрия на клетчатой бумаге. Построение фигуры, симметричной данной относительно оси симметрии. - 4 класс. - Симметричность как свойство математических отношений. В заданиях, предлагаемых программой В. Н. Рудницкой, используются следующие методы и приемы: - практический метод построения симметричных пар; - наглядно-практический; - объяснительно-иллюстративный. Вывод: Таким образом, анализ заявленных программ по данной теме позволил сделать вывод о том, что по программам Н.Б. Истоминой, М.И. Моро и В.Н. Рудницкой тема «Симметрия» распределена во времени и по всем годам обучения, в отличие от программы Л.Г. Петерсон, где тема изучается только в 3-ем классе. Так, по программе Истоминой Н.Б. изучение данной темы предусмотрено в 1-м и 3-м классах, во 2-м и 4-м классе новых сведений по данному вопросу не дается, но материал, изученный в предыдущих классах, включается в темы учебников (2-й и 4-й классы) для повторения и закрепления, имеющихся ЗУНов по теме «Симметрия». В программе Рудницкой В.Н. только во 2-ом классе отсутствуют темы, непосредственно связанные с симметрией. Программы предусматривают знакомство учащихся со следующими понятиями: «симметричные фигуры», «ось симметрии», «фигуры, имеющие несколько осей симметрии». Эти понятия вводятся в 1-м классе по программам Истоминой Н.Б. и Рудницкой В.Н.. В 3-м классе и Н.Б.Истомина, и В.Н. Рудницкая вводят в программу тему «Построение симметричных фигур с помощью чертежных инструментов». По программе Л.Г. Петерсон все названные понятия и темы включены в учебник для 3 класса. В отличие от программы Истоминой Н.Б. и Петерсон Л.Г. Рудницкая В.Н. в курсе «математика 1 класс» включает построение симметричных точек, отрезков, многоугольников практическим путем. В 3-м классе перед изучением темы «Построение симметричных фигур с помощью чертежных инструментов» изучается тема «Симметрия на клетчатой бумаге». В 4-м классе данный материал выводится на качественно новый уровень изучения. Здесь изучается важнейшее свойство математических отношений - симметричность. Исходя из этого, можно заключить, что объем учебного материала по теме «Симметрия» по трём программам не равнозначен. По программе Рудницкой В.Н. отведено большее количество часов данному вопросу, чем в программах Петерсон Л.Г. и Истоминой Н.Б. Качественное изучение данной темы также различаются. В курсе Рудницкой В.Н. даются более глубокие знания по теме симметрияКачественное изучение данной темы также различается. В курсе Рудницкой В.Н. даются более глубокие знания по теме «Симметрия». К концу 4-го класса по анализируемым программам предъявляются следующие требования к ЗУ Нам учащихся по теме «Симметрия»: узнавать симметричные фигуры; строить фигуру, симметричную данной относительно оси симметрии. Кроме того, по программе Рудницкой В.Н. выделяется еще и такое требование - уметь строить граф отношения симметричности, а также определять по графу обладает ли он данным отношением. Основным методом при изучении данной темы по обеим программам является наглядно-практический. Сделанные выводы позволяют нам говорить о том, что преследуя цель: развитие геометрических и пространственных представлений у учащихся и соблюдение преемственности между начальным и среднем звеном, В.Н. Рудницкая и Т.В. Юдачева постарались представить наиболее широкие и глубокие знания по теме «Осевая симметрия». 2. Методические подходы к использованию наглядно-практического метода в процессе изучения симметрии в начальном курсе математики Как показал анализ методического подхода к данной теме, наглядно-практический метод имеет важное место на уроках математики на различных этапах изучения темы «Симметрия». Однако, как показывает анализ учебников, предложенных заданий недостаточно на наш взгляд, для осознанного усвоения понятия «Симметрия». В соответствии с логикой изложения методического материала будем рассматривать задания по каждой программе в отдельности. Так в рамках действия каждой программы по данной теме и концептуальных положений, лежащих в ее основе, нами были разработаны задания, которые могут быть использованы на разных этапах изучения данной темы. Задания, направленные на изучение темы «Симметрия» в соответствии с программой Л.Г. Петерсон. Тема «Преобразование фигур» в 3-ем классе. Подготовительный этап. Задание 1. Слайд 21 Цель задания: подготовить учащихся к знакомству с преобразованием фигур. «Возьмите заготовки с ракетой. - из каких геометрических фигур оно состоит? - начерти по клеткам такую же ракету в тетради и перенеси ее вправо на десять клеток.» Этап введения. Задание 1. Слайд 22 Цель задания: актуализировать знания учащихся по теме «Преобразование фигур». «- перенесите данную фигуру на семь клеток вправо, а потом на три клетки вниз – результаты преобразований черти карандашом разных цветов». Этап закрепления. Задание 1. Слайд 23 Цель задания: закрепить полученные знания по теме «Преобразование фигур». «- нарисуй квадрат стороной в четыре клеточки, сначала перенеси его на десять клеток вправо, а потом на три клетки влево. - каким одним преобразованием можно заменить эти два». Задание 2. Слайд 24 Цель задания: закрепить полученные знания по теме «Преобразование фигур». «-построй треугольник симметричный треугольнику АВС относительно стороны ВС, а потом полученный треугольник перенеси на четыре клетки вправо». Тема «Симметрия». Этап подготовки. Задание 1. Слайд 25 Цель задания: подготовить учащихся к знакомству с понятием «Симметрия». «Перед вами карточка с изображением бабочки, разделите вертикальной чертой этот рисунок на две части. Что можно сказать о частях рисунка?» Этап введения. Задание 1. Слайд 26 Цель задания: практически познакомить учащихся с темой «Симметрия». «- Практическая работа. Возьмите лист бумаги и согните его пополам, проколите ножкой циркуля, что у вас получилось? Обозначьте их А и В и соедините отрезком. Точку пересечения этого отрезка с линией сгиба обозначьте буквой О. Линия сгиба в математике называется осью симметрии. Давайте измерим расстояние от точек А и В до линии симметрии. Теперь возьмем угольник и приложим к углу, который образуется отрезком АВ и осью симметрии (получился прямой угол),такие прямы называются перпендикулярными. Давайте сформулируем свойства симметричных точек. Симметричные точки расположены на прямой перпендикулярной оси симметрии на равном расстоянии от нее». Этап закрепления. Задание 1. Слайд 27 Цель задания: закрепить полученные знания по теме «Симметрия». «Какие точки в математике называются симметричными? Построй точки симметричные данным, относительно прямой L. Проверь правильность построения с помощью кальки». Тема «Симметричные фигуры» Подготовительный этап. Задание 1. Слайд 28 Цель задания: подготовить учащихся к знакомству с симметричными фигурами. «Перед вами на линованной бумаге геометрические фигуры, по каким признакам вы их можете разделить на две группы?». Задание 2. Слайд 29 Цель задания: подготовить учащихся к знакомству с симметричными фигурами. «Возьмите рисунок из конверта, положите на стол, рядом поставьте зеркало, что вы можете сказать об этом рисунке?» Этап введения. Задание 1. Слайд 30 Цель задания: актуализировать знания учащихся по теме «Симметричные фигуры». «Дорисуй симметричные фигуры». Задание 2. Слайд 31 Цель задания: актуализировать знания учащихся по теме «Симметричные фигуры». «Какие фигуры на рисунке симметричны относительно прямой L?» Этап закрепления. Задание 1. Слайд 32 Цель задания: закрепить полученные знания по теме «Симметричные фигуры». «Построй фигуры симметричные данным относительно прямой L. Проверь правильность построения с помощью кальки». Задания, направленные на изучение темы «Симметрия» в соответствии с программой Н.Б. Истоминой. Тема «Симметричные фигуры» (1-ый класс). Подготовительный этап. Задание 1. Слайд34 Цель задания: подготовить учащихся к знакомству с симметричными фигурами. «На рисунке изображены половинки букв, используя зеркало назови эти буквы». Этап введения. Задание 1. Слайд 35 Цель задания: актуализировать знания учащихся по теме «Симметричные фигуры». «Наложи прозрачную бумагу на карточку с изображением фигур. Переведи и вырежи их, сложи по прямой линии, что ты наблюдаешь? (это симметричные фигуры). Прямая линия, по которой ты сложил фигуры – ось симметрии». Задание 2. Слайд 36 Цель задания: актуализировать знания учащихся по теме «Симметричные фигуры». «По какому признаку фигуры разбиты на две группы? (1ая – яблоко, колокольчик, бабочка, снеговик; 2ая группа – чайник, варежка». Задание 3. Слайд 37 Цель задания: актуализировать знания учащихся по теме «Симметричные фигуры». «Сколько осей симметрии имеют данные фигуры? (квадрат, овал, круг)». Этап закрепления. Задание 1. Слайд 38 Цель задания: закрепить полученные знания по теме «Симметричные фигуры». «Проверь, прав ли Миша говоря, что эти фигуры симметричны? (прямоугольник, ромб, четырехугольник, равнобедренный треугольник, круг)». Тема «Симметричные фигуры» (2-ой класс). Этап закрепления. Задание 1. Слайд 39 Цель задания: закрепить знания, полученные в 1-ом классе по теме «Симметричные фигуры». «Проверь, симметричны ли эти изображения (снеговик, звездочка, снежинка, шляпа, кленовый лист». Задание 2. Слайд40 Цель задания: закрепить знания, полученные в 1-ом классе по теме «Симметричные фигуры». «Дорисуй симметричные фигуры». Тема «Симметричные фигуры» (3-ий класс). Подготовительный этап. Задание 1. Слайд41 Цель задания: подготовить учащихся к знакомству с понятием «ось симметрии». «Вспомни по какому признаку фигуры разбиты на две группы. (лист, шляпа, колокольчик; варежка, кувшин». Этап введения. Задание 1. Слайд 42 Цель задания: познакомить учащихся с понятием «ось симметрии». «Внимательно посмотрите на фигуры лежащие перед вами (треугольник, прямоугольник). Возьмите треугольник, проведите в нем ось симметрии, сколько таких осей можно провести? А теперь работаем с прямоугольником. Сколько здесь можно провести осей симметрии?». Задание 2. Слайд 43 Цель задания: познакомить учащихся с понятием «ось симметрии». «На доске изображена точка А. - что же необходимо сделать, чтобы построить симметричную точку? (провести прямую, т.е. ось симметрии). - положите угольник так, чтобы одна сторона прошла по линии оси, а другая через точку А. Точку пересечения прямой с осью симметрии обозначим буквой О. Отложим отрезок ОВ=АО. Точки А и В симметричны относительно данной прямой. А как это проверить? Берем циркуль, измеряем АО, если длина этого отрезка совпадает с длиной АВ, то построение симметричное.» Этап закрепления. Задание 1. Слайд 44 Цель задания: закрепить полученные знания по теме «Симметричные фигуры», связанные с понятием «ось симметрии». «Постройте две точки А и В. Проведите ось симметрии. Постройте симметричные точки СD». Тема «Симметричные фигуры» (4-ый класс). Этап закрепления. Задание 1. Слайд 45 Цель задания: закрепить знания, полученные в 1-3 классе по теме «Симметричные фигуры». «Постройте симметричные точки а) если их две; б) если точка расположена на прямой». Задания, направленные на изучение темы «Симметрия» в соответствии с программой В.Н. Рудницкой. Слайд46 Тема «Зеркальное отражение предметов» (1-ый класс) Подготовительный этап. Задание 1. Слайд 47 Цель задания: провести пропедевтическую подготовку по знакомству учащихся с симметричными фигурами посредством зеркального отражения предметов. «В тихую погоду в реке как в зеркале отражается берег. Найдите дерево, елочку, цветок и их отражение в воде». Этап введения. Задание 1. Слайд48 Цель задания: познакомить учащихся с симметричными фигурами посредством зеркального отражения. «Поставьте зеркало сверху, справа, снизу от каждой цифры и посмотрите на ее отражение в зеркале (1, 2, 3, 4, 5, 6, 7, 8, 9, 0). Какие цифры выглядят совершенно одинаково?» Этап закрепления. Задание 1. Слайд 49 Цель задания: закрепить полученные знания, связанные с симметричными фигурами и их зеркальным отражением. «Проверьте с помощью зеркала, поставив его слева и справа, что буквы А, Ж, М, Н, О, П, Т, Ф, Х, Ш не изменяются.» Тема «Симметрия» (1-ый класс). Подготовительный этап. Задание 1. Слайд50 Цель задания: подготовить учащихся к знакомству с симметричными фигурами, используя зеркало. «На рисунке изображены «половинки» букв. Мысленно представьте себе недостающие половинки. Назовите их. Затем проверьте себя с помощью зеркала». Этап введения. Задание 1. Слайд51 Цель задания: познакомить учащихся с осью симметрии. «Выложи квадраты относительно оси симметрии». Этап закрепления. Задание 1. Слайд52 Цель задания: закрепить полученные знания, связанные с симметричными фигурами и понятием ось симметрии. «Найди ось симметрии пары симметричных отрезков, пары симметричных концов отрезков, оси симметрии фигуры». Тема «Симметрия» (2-ой класс). Этап закрепления. Задание 1. Слайд 53 Цель задания: закрепить знания, полученные в 1-ом классе по теме «Симметрия». «Проверь, действительно ли звезда имеет пять осей симметрии, а квадрат четыре?» Тема «Симметрия на клетчатой бумаге» (2-ой класс). Подготовительный этап. Задание 1. Слайд54 Цель задания: подготовить учащихся к знакомству с симметрией на клетчатой бумаге. «Рядом с нарисованной точкой поставим прямоугольное зеркальце ребром на ось симметрии. Это и будет точка симметричная данной. Пересчитав клеточки убедимся в том, что точка и ее образ находятся на одном и том же расстоянии от оси симмметрии». Этап введения. Задание 1. Слайд 55 Цель задания: познакомить учащихся симметрией на клетчатой бумаге. «Поставь зеркало ребром на ось симметрии АВ, определи на расстоянии скольких клеток расположены точки симметричные точкам на чертеже». Задание 2. Слайд 56 Цель задания: познакомить учащихся симметрией на клетчатой бумаге. «Выдели цветным карандашом точки симметричные данным». Этап закрепления. Задание 1. Слайд 57 Цель задания: закрепить полученные знания по теме «Симметрия на клетчатой бумаге». «Скопируй рисунок в тетрадь и изобрази фигуры симметричные данным» Тема «Симметрия на клетчатой бумаге» (4-ый класс). Этап закрепления. Задание 1. Слайд 58 Цель задания: закрепить знания, полученные по теме «Симметрия». «Правильно ли проведены оси симметрии в каждой фигуре? (ромб 2 оси, круг 2 оси, треугольник 3 оси, квадрат 1 ось)». Задание 2. Слайд 59 Цель задания: закрепить знания, полученные по теме «Симметрия». «Перечерти в тетрадь фигуры и построй им симметричные». Вывод: Исследовав методические подходы к использованию наглядно-практического метода в процессе изучения темы «Симметрия» в начальном курсе математики, можно сделать вывод, что наиболее полно исследуемая тема охватывается при подаче материала ученикам, опираясь на программу В.Н. Рудницкой. Список литературы Федорова, О. А., Коновалова, Н. В. // Совершенствование экологообразовательной деятельности в Саратовской области : Межвуз. сб. науч. тр. Саратов : ИЦ «Наука». 2018. Выпуск 16. С. 96-102 Учебники по математике для начальных классов Школа России, Моро, 1 - 4 класс в 2х частях. Учебники по математике для начальных классов Петерсон. Учебники по математике для начальных классов Истомина. Учебники по математике для начальных классов Аргинская. Царева Светлана Евгеньевна Методика преподавания математики. Аргунов,Б.И. Преобразования плоскости : учеб. пособие для студентов-заочников педагогических институтов / Б.И.Аргунов. – М. : Просвещение, 1976. – 80 с. Яглом И.М* Геометрические преобразования: Движения и преобразования подобия. М.: Изд-во технико-теоретической литературы, 1955, т. I. - 282 с.175." Яглом И.М. О школьном курсе геометрии. Математика в школе, 1968^ № 2, с. 53-58. Методические рекомендации для учителей, начинающих работать по курсу математики Л.Г. Петерсон «Учусь учиться».Вейль Г., Симметрия, пер. с англ., М., 1968. – 192 с.: ил.А.В. Белошистая. Методика обучения математики в начальной школе, М., «Владос», 2007. |
