Самостаятельная (2). Преобразование скорости и ускорения при переходе к новой системе отсчета. Связь между угловыми и линейными скоростями и ускорениями
 Скачать 352.19 Kb. Скачать 352.19 Kb.
|
|
МИНИСТРЕСТВО ПО РАЗВИТИЮ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ И КОМУНИКАЦИЙ РЕСПУБЛИКИ УЗБЕКИСТАНА ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ ИМЕНИ МУХАММАД АЛЬ-ХОРАЗМИЙ САМОСТОЯТЕЛЬНАЯ РАБОТА ТЕМА: Преобразование скорости и ускорения при переходе к новой системе отсчета. Связь между угловыми и линейными скоростями и ускорениями. Студента группы:075-20 Выполнил(а):Кантемир Максим Проверил: _________________ ТАШКЕНТ-2021 ПЛАН: Преобразования Галилея Угловая скорость и угловое ускорение Связь линейных и угловых характеристик движения Преобразования Галилея Принцип относительности Галилея Следствия преобразований Галилея Угловая скорость и угловое ускорение Угловое перемещение Угловая скорость Угловое ускорение Связь линейных и угловых характеристик движения Линейная скорость Связь ускорения и угловой скорости при равномерном вращении Преобразования Галилея - это уравнения, связывающие координаты и время некоторого события в двух инерциальных системах отсчета. Событие определяется местом, где оно произошло (координаты x, y, z), и моментом времени t, когда произошло событие. Событие полностью определено, если заданы четыре числа: x,y,z,t - координаты события. Пусть материальная точка m в системе отсчета К в момент времени t имела координаты x, y, z. Найдем координаты t', x', y', z' этого события в системе отсчета К', которая движется относительно системы К равномерно и прямолинейно вдоль оси х с постоянной скоростью V . Выберем начало отсчета времени так, чтобы в момент времени t =0 начала координат совпадали. Оси х и х' направлены вдоль одной прямой, а оси у и у', z и z' - параллельны. Тогда очевидно: x=x’+vt Кроме того, ясно, что для наших систем координат y=y’, z=z’ В механике Ньютона предполагается, что t= t’ т.е. время течет одинаково во всех системах отсчета. Полученные четыре формулы и есть преобразования Галилея: x=x’+vt y=y’ z=z’ t= t’ Принцип относительности Галилея: никакими механическими опытами нельзя установить, покоится ли данная система отсчета или движется равномерно и прямолинейно. Это утверждение согласуется с преобразованиями Галилея. Продифференцируем их 2 раза по времени. После первого дифференцирования получим закон сложения скоростей:
     Второе дифференцирование дает Второе дифференцирование дает
Ускорение материальной точки одинаково в обеих системах отсчета a=a’ . Кроме того, силы, действующие на частицу, одинаковы, изменяется и величина m (по определению, это масса покоя). Значит, в системе К второй закон Ньютона ma=F такой же, как и в системе К' ma=F т.к. a=a’ - следствие преобразований Галилея. Иными словами, на теоретическом уровне, принцип относительности Галилея можно сформулировать так : Законы механики одинаково выглядят во всех инерциальных системах отсчета. Следсвия преобразований Галилея Ход времени одинаков в обеих системах отсчета. t = t' – абсолютный характер времени в механике Ньютона. Равенство масс в обеих системах отсчета. m = m'- абсолютный характер массы во всех инерциальных системах отсчета. 3) Равенство ускорений масс в обеих системах отсчета. a=a’ абсолютный характер ускорения во всех инерциальных системах отсчета. 4) Равенство сил взаимодействия материальных точек в инерциальных системах отсчета. FF’ -сила инвариантна (неизменна) относительно преобразований Галилея. Неудовлетворительность механики Ньютона при больших скоростях Рассмотрим с точки зрения преобразований Галилея движение света. Опубликованные в 1881 г. результаты опытов, выполненных американским физиком А. Майкельсоном, находятся в противоречии с только что полученной нами формулой: галилейский закон сложения скоростей не годится для света. Скорость света оказалась одинаковой в разных системах отсчета! В системе К' его скорость v’X= c Тогда, используя полученный закон сложения скоростей из для скорости света в системе К, мы найдем: В 1895 г. французский математик, физик и философ А. Пуанкаре впервые выступил с новаторским предложением о невозможности никакими физическими опытами (не только механическими, как в принципе относительности Галилея) зарегистрировать абсолютное движение. В 1902 г. он же публикует в книге "Наука и гипотеза" утверждение об отсутствии абсолютного времени, т.е. t ≠ t'. Законченная теория, позволяющая описывать движение частиц со скоростями vc, была опубликована в 1905 г. в работах А. Пуанкаре и А. Эйнштейна. Угловое перемещение dвекторная величина, модуль которой равен углу поворота, а направление совпадает с направлением поступательного движения правого винта. Угловая скорость - векторная величина равная первой производной угла поворота тела по времени 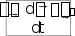 Вектор направлен вдоль оси вращения так же как и вектор d , т.е. по правилу правого винта. Угловое ускорение - векторная величина, равная первой производной угловой скорости по времени 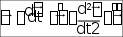 Вектор направлен вдоль оси вращения в сторону вектора приращения угловой скорости (при ускоренном вращении вектор сонаправлен вектору , при замедленном — противонаправлен ему). 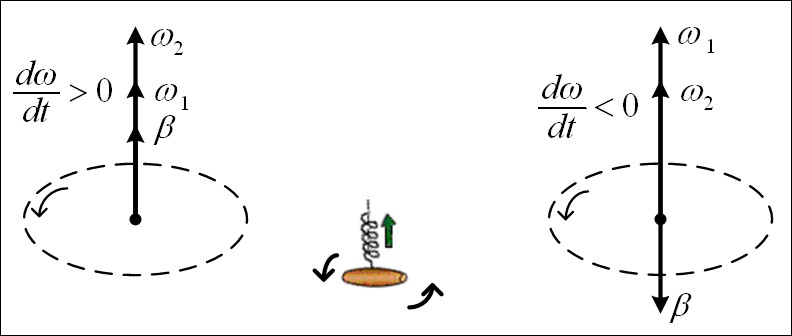 Линейная скорость точки связана с угловой скоростью и радиусом траектории соотношением 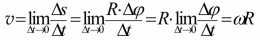 При равномерном вращении 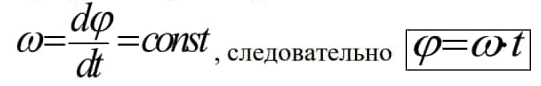 Равномерное вращение можно характеризовать периодом вращения T — временем, за которое точка совершает один полный оборот, 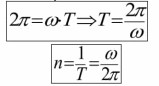 Связь ускорения и угловой скорости при равномерном вращении: 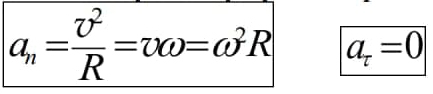 При равноускоренном вращении: Угловое ускорение постоянное const Угловая скорость 0 t Угловое перемещение 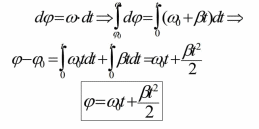 Нормальное и тангенциальное ускорение: 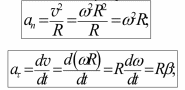 Таким образом, при движении материальной точки по окружности для описания еѐ движения можно пользоваться как линейными, так и угловыми величинами. Однако при вращении твѐрдого тела удобно использовать угловые величины, а не линейные, поскольку уравнения движения разных точек, выраженные в угловых величинах, одинаковы для всех точек тела, в то время как при пользовании линейными величинами они различны. Используемая литература 1. Огурцов Н.А. Курс лекций по физике, Харьков,2007г. 2. Колмаков Ю.Н. Курс лекций по физике, Тула, 2002г. 3. Оплачко Т.М.,Турсунметов К,А. Физика, Ташкент, 2007г. 4. К.П.Абдурахманов, О.Э.Тигай, В.С.Хамидов Курс лекций по физике (приложение к мультимедийным лекциям), Ташкент, 2010 г. 5. Любутина Л.Г., Нагаев В.Б., Бекетов В.Г. Конспектлекций по дисциплине Физика, Россия,2005г. 6. Трофимова Т.И. Курс физики: Учеб. пособие для вузов. – М.: Высш. шк., 2006. – 542 с. 7. Детлаф А.А., Яворский Б.М. Курс физики: Учебное пособие для втузов. – 4-е изд., испр. – М.: Высш. шк., 2002. – 718 с. 8. Савельев И.В. Курс общей физики: В 5 кн.: кн. 3: Учебное пособие для втузов. – М.: ООО «Издательство Астрель», 2004. – 336 с. 9. Курс мультимедийных лекций по физике К.П.Абдурахманов О.Э.Тигай В.С.Хамидов ТАШКЕНТ 2012 10. В.А. Алешкевич, Л.Г. Деденко, В.А. Караваев. МЕХАНИКА. М.: ACADEMIA. 2004. 480 c. (Университетский курс общей физики). |
