Документ Microsoft Office Word. Презентация научного или практического доклада в электронном виде Интерактивные презентации

Название	Презентация научного или практического доклада в электронном виде Интерактивные презентации
Анкор	Документ Microsoft Office Word.docx
Дата	29.08.2018
Размер	113.21 Kb.
Формат файла
Имя файла	Документ Microsoft Office Word.docx
Тип	Презентация #23723

Тема 20

Типы презентаций:

CD-презентация; Буклет; Выставочный стенд; Виртуальные туры; Веб-представительство; Электронные визитные карточки; Презентация научного или практического доклада в электронном виде; Интерактивные презентации.

Электронная презентация – это набор слайдов, который служит иллюстративным материалом для лекций, докладов и выступлений. На слайдах презентации могут размещаться различные объекты: рисунки, текст, таблицы, диаграммы.

Правила оформления презентаций: При построении презентации всегда необходимо отталкиваться от целей презентации и от условий прочтения. Дизайн должен быть простым и лаконичным. Основная цель – это читаемость с экрана, а не субъективная красота. При этом не надо впадать в другую крайность и писать на белых листах чёрными буквами. На слайдах должны быть тезисы – они сопровождают подробное изложение мыслей докладчика, но не наоборот. Точку в конце заголовка не ставить. А между предложениями она требуется. Не писать длинные заголовки.

Ошибки докладчиков:Выступление длится слишком долго. (должно хватать 10!-15 минут);Выступление по пунктам убивает живое общение;Отказ от репетиций (на каждый час презентации – 10 часов репетиций); Чтение слайдов; Монотонная речь и игнорирование жестов

Заключение выступления:Люди помнят, что сказано последним;Подведите итог;Заключение должно быть коротким;В конце презентации смотрите на аудиторию, не подглядывайте в свои конспекты, так как это отвлекает внимание от ваших слов.

Структура презентации на защите: Название доклада;Постановка задачи;Описание проекта целиком. Роль и место в проекте.Анализ ТЗ(техническое задание): существующие аналоги и наработки;Ход работы. Решённые научные и технические задачи;Достигнутые результаты (наглядно представить показатели, продемонстрировать работающий проект/устройство).Выводы и результаты исследования/работы.Завершение.

Тема 5

Ве́кторная гра́фика — способ представления объектов и изображений в компьютерной графике, основанный на использовании элементарных геометрических объектов, таких как точки, линии, сплайны и многоугольники. Термин используется в противоположность к растровой графике, которая представляет изображение как матрицу фиксированного размера, состоящую из точек (пикселей) со своими параметрами.

Сплайн (англ. spline - планка, рейка) - функция, область определения которой разбита на конечное число отрезков, на каждом из которых сплайн совпадает с некоторым алгебраическим полиномом. Максимальная степень из использованных полиномов называется степенью сплайна. Разность между степенью сплайна и получившейся гладкостью называется дефектом сплайна. Например, непрерывная ломаная есть сплайн степени 1 и дефекта 1.Сплайны имеют многочисленные применения как в математической теории, так и в разнообразных вычислительных приложениях. В частности, сплайны двух переменных интенсивно используются для задания поверхностей в различных системах компьютерного моделирования. Основной элемент изображения — линия.Линия представлена в памяти ПК несколькими параметрами и в этом виде занимает гораздо меньше места, чем растровая линия состоящая из точек, для каждой из которых требуется ячейка памяти.Линия — элементарный объект векторной графики. Любой сложный объект можно разложить на линии, прямые или кривые. Поэтому часто векторную графику называют объектно-ориентированной.Свойства линии:Форма, Толщина,Цвет,Стиль (пунктир, сплошная) Замкнутые линии имеют свойство заполнения — цветом, текстурой, узором и т.п. Каждая незамкнутая линия имеет 2 вершины, называемые узлами. С помощью узлов можно соединять линии между собой.

Математические основы векторной графикиРассмотрим подробнее способы представления различных объектов в векторной графике.Точка — этот объект на плоскости представляется двумя числами (х, у), указывающими его положение относительно начала координат.Прямая линия. Ей соответствует уравнение y=kx+b. Указав параметры k и b, всегда можно отобразить бесконечную прямую линию в известнойсистеме координат, то есть для задания прямой достаточно двух параметров.Отрезок прямой. Он отличается тем, что требует для описания еще двух параметров – например, координат x₁ и х₂ начала и конца отрезка.

Кривая второго порядка. К этому классу кривых относятся параболы, гиперболы, эллипсы, окружности, то есть все линии, уравнения которых содержат степени не выше второй. Кривая второго порядка не имеет точек перегиба.Прямые линии являются всего лишь частным случаем кривых второго порядка. Формула кривой второго порядка в общем виде может выглядеть, например, так: x²+a₁y²+a₂xy+a₃x+a₄y+a₅=0.Таким образом, для описания бесконечной кривой второго порядка достаточно пяти параметров. Если требуется построить отрезок кривой, понадобятся еще два параметра.

Кривая третьего порядка. Отличие этих кривых от кривых второго порядка состоит в возможном наличии точки перегиба. Например, график функции у= x³ имеет точку перегиба в начале координат.Именно эта особенность позволяет сделать кривые третьего порядка основой отображения природных объектов в векторной графике. Например, линии изгиба человеческого тела весьма близки к кривым третьего порядка. Все кривые второго порядка, как и прямые, являются частными случаями кривых третьего порядка.В общем случае уравнение кривой третьего порядка можно записать так:x³+a₁y³+a₂x²y+a₃xy²+a₄x²+a₅y²+a₆xy+a₇x+a₈y+a₉=0.Таким образом, кривая третьего порядка описывается девятью параметрами. Описание ее отрезка потребует на два параметра больше.

Кривые Безье. Это особый, упрощенный вид кривых третьего порядкаМетод построения кривой Безье (Bezier) основан на использовании пары касательных, проведенных к отрезку линии в ее окончаниях. Отрезки кривых Безье описываются восемью параметрами, поэтому работать с ними удобнее. На форму линии влияет угол наклона касательной и длина ее отрезка.Таким образом, касательные играют роль виртуальных “рычагов”, с помощью которых управляют кривой.
Тема 6

Цвет в векторной графикеРазличные векторные форматы обладают различными цветовыми возможностями. Простейшие форматы, которые могут не содержать вообще никакой информации о цвете, используют цвет по умолчанию тех устройств, на которые они выводятся, другие форматы способны сохранять данные о полном тридцати двух битном цвете. Какую бы цветовую модель не применял бы векторный формат, на размер файла он не влияет, кроме тех случаев, когда файл содержит растровые образы.В обычных векторных объектах значение цвета относится ко всему объекту в целом. Цвет объекта хранится в виде части его векторного описания. Некоторые векторные файлы могут создать растровый эскиз изображений хранящихся в них. Эти растровые картинки, иногда называемые краткими описаниями изображений, обычно представляют собой эскизы векторных рисунков в целом. Краткое описание изображения, особенно полезно в ситуациях, когда вы не хотите открывать весь файл, чтобы посмотреть, что в нем хранится или когда вы не можете видеть векторный рисунок во время его использования. Первая ситуация возникает, когда вам необходимо найти файл с помощью одной из многих специально разработанных для этого программ. Для облегчения поиска нужного векторного файла такие программы могут считывать растровый эскиз изображения и другие характеристики, например, векторный формат, время создания, битовую глубину изображения и так далее. Вторая ситуация возникает, когда в каком-либо издательском пакете помещается на страницу векторный рисунок. Изображение, которое вы увидите, будет растровым эскизом настоящего векторного рисунка, у которого нельзя изменить размер, обрезать или как-то иначе обработать изображение. За эскизы изображения приходится расплачиваться памятью, т.к. эскизы - это растровая версия рисунков, а растровые данные используют много памяти компьютера.

Достоинства векторной графики

Небольшой размер файла при относительно несложной детализации изображения.
Возможность неограниченного масштабирования без потери качества.
Возможность перемещения, вращения, растягивания, группировки и т.д.так же без потери качества.
Возможность позиционирования объектов по оси, перпендикулярной плоскости экрана (по оси z — «выше», «ниже», «выше всех», «ниже всех»).
Возможность выполнения булевых преобразований над объектами — сложение, вычитание, пересечение, дополнение.
Управление толщиной линий при любом масштабе изображения.

Недостатки векторной графики:

Большой размер файла при сложной детализации изображения. (Бывают случаи, что изза множства мелких сложных деталей размер векторного изображения гораздо превышает размер его растровой копии)
Трудность передачи фотореалистичного изображения (следует из 1го недостатка)
Проблемы совместимости программ, работающих с векторной графикой, при этом не все программы открывают (или корректно отображают) даже «общепринятые» форматы (такие как eps), созданные в других редакторах.

Графика в интернете.

- формат GIF поддерживает только 256-битовый цвет

- формат HNG (Portable Network Graphics) поддерживет 48-битовые цветные и 16-битовые чёрно-белые изображения

- формат PNG поддерживает альфа-каналы, позволяющие устанавливать уровни…………..

- формат FlashPix поддерживает многоуровневую организацию файла.

- формат FIF (Fractal Image Format) на основе фрактальной компрессии.

- JPEG 2000 поддерживает потоковость, альфа-каналы (alpha channel)/

- DjVu поддерживает сжатие отдельно графического и текстового слоя.

редактируемая двумерная графика для Интернета

Microsoft, Hewlett-Packard и три фирмы, специализирующиеся в области ПО, представили на рассмотрение консорциума World Wide Web (W3C) стандарт, предназначенный для реализации высококачественной редактируемой двумерной векторной графики в Интернете.

Коротко о VML:

С помощью языка векторной разметки (Vector Markup Language - VML) Web-дизайнеры смогут без труда редактировать, вырезать и вставлять векторные изображения в прикладные программы. Такая возможность, по мнению Стива Склеповича, менеджера по продуктам компании Microsoft, чрезвычайно нужна пользователям.

В отличие от растровой графики, представляющей собой изображения, образованные матрицами пикселов, векторные изображения состоят из линий, квадратов и других геометрических объектов.

Благодаря VML дизайнеры Web-узлов смогут изменять масштаб векторных изображений на Web-страницах и загружать графику значительно быстрее, чем изображения в растровом формате.

«Формат VML появился на базе языка Extensible Markup Language (XML - расширяемый язык разметки), дополняющего HTML. Web-дизайнеры получили в свое распоряжение более гибкий инструмент, который позволяет создавать собственные теги, сообщают представители компаний.
Тема 2

Изобразительная компьютерная графика

Объекты: синтезированные изображения. Задачи:
 построение модели объекта и генерация изображения,
 преобразование модели и изображения,
 идентификация объекта и получение требуемой информации.

Обработка и анализ изображений

Объекты: дискретное, числовое представление фотографий. Задачи:
 повышение качества изображения,

 оценка изображения - определение формы, местоположения, размеров и других параметров требуемых объектов,

 распознавание образов - выделение и классификация свойств объектов (обработка аэрокосмических снимков, ввод чертежей, системы навигации, обнаружения и наведения).

Итак, в основе обработки и анализа изображений лежат методы представления, обработки и анализа изображений плюс, естественно, изобразительная компьютерная графика хотя бы для того, чтобы представить результаты.

Когнитивная компьютерная графика

Только формирующееся новое направление, пока недостаточно четко очерченное. Это компьютерная графика для научных абстракций, способствующая рождению нового научного знания. База - мощные ЭВМ и высокопроизводительные средства визуализации. Общая последовательность познания заключается в, возможно циклическом, продвижении от гипотезы к модели (объекта, явления) и решению, результатом которого является знание (рис. 0.1.1).

основная проблема и задача когнитивной компьютерной графики - создание таких моделей представления знаний, в которых можно было бы однообразно представлять как объекты, характерные для логического (символического, алгебраического) мышления, так и объекты, характерные для образного мышления.

Другие важнейшие задачи:

 визуализация тех знаний, для которых не существует (пока ?) символических описаний,

 поиск путей перехода от образа к формулировке гипотезы о механизмах и процессах, представленных этими (динамическими) образами на экране дисплея.

Анализ сцен

Предмет: исследование абстрактных моделей графических объектов и взаимосвязей между ними. Объекты могут быть как синтезированными, так и выделенными на фотоснимках. Первый шаг в анализе сцены - выделение характерных особенностей, формирующих графический объект(ы). Примеры: машинное зрение (роботы), анализ рентгеновских снимков с выделением и отслеживанием интересующего объекта, например, сердца. Итак, в основе анализа сцен (перцептивной компьютерной графики) находятся изобразительная графика + анализ изображений + специализированные средств

Тема 4

Интенсивность тона (так называемую светлоту) принято подразделять на 256 уровней. Большее число градаций не воспринимается зрением человека и является избыточным. Меньшее число ухудшает восприятие изображения (минимально допустимым для качественной полутоновой иллюстрации принято значение 150 уровней). Нетрудно подсчитать, что для воспроизведения 256 уровней тона достаточно иметь размер ячейки растра 256 = 16 х 16 точек.При выводе копии изображения на принтере или полиграфическом оборудовании линиатуру растра выбирают, исходя из компромисса между требуемым качеством, возможностями аппаратуры и параметрами печатных материалов. Для лазерных принтеров рекомендуемая линиатура составляет 65—100 dpi, для газетного производства — 65—85 dpi, для книжно—журнального — 85—133 dpi, для художественных и рекламных работ — 133—300 dpi.

Динамический диапазон. Качество воспроизведения тоновых изображений принято оценивать динамическим диапазоном (D). Это оптическая плотность, численно равная десятичному логарифму величины, обратной коэффициенту пропускания (для оригиналов, рассматриваемых “на просвет”, например слайдов) или коэффициенту отражения (для прочих оригиналов, например полиграфических отпечатков).Для оптических сред, пропускающих свет, динамический диапазон лежит в пределах от 0 до 4. Для поверхностей, отражающих свет, значение динамического диапазона составляет от 0 до 2. Чем выше динамический диапазон, тем большее число полутонов присутствует в изображении и тем лучше качество его восприятия.В цифровом мире компьютерных изображений термином пиксел обозначают несколько разных понятий. Это может быть отдельная точка экрана компьютера, отдельная точка напечатанная на лазерном принтере или отдельный элемент растрового изображения. Эти понятия не одно и тоже, поэтому чтобы избежать путаницы следует называть их следующим образом: видео пиксел при ссылке на изображение экрана компьютера; точка при ссылке на отдельную точку, создаваемую лазерным принтером. Существует коэффициент прямоугольности изображения, который введен специально для изображения количества пикселов матрицы рисунка по горизонтали и по вертикали.Возвращаясь к аналогии с листом бумаги можно заметить, что любой растровый рисунок имеет определенное количество пикселов в горизонтальных и вертикальных рядах. Существуют следующие коэффициенты прямоугольности для экранов: 320х200, 320х240, 600х400, 640х480, 800х600 и др. Этот коэффициент часто называют размером изображения. Произведение этих двух чисел дает общее количество пикселов изображения.

Существует прямая зависимость размера файла растрового изображения. Чем больше в изображении пикселов, тем больше размер файла. Разрешающая способность изображения на величину файла никак не влияет. Разрешающая способность оказывает эффект на размер файла только при сканировании или редактировании изображений. Связь между битовой глубиной и размером файла непосредственная. Чем больше битов используется в пикселе, тем больше будет файл. Размер файла растровой графики сильно зависит от формата выбранного для хранения изображения. При прочих равных условиях, таких как размеры изображения и битовая глубина существенное значение имеет схема сжатия изображения. Например, BMP файл имеет, как правило, большие размеры, по сравнению с файлами PCX и GIF, которые в свою очередь больше JPEG файла.Многие файлы изображений обладают собственными схемами сжатия, также могут содержать дополнительные данные краткого описания изображения для предварительного просмотра.
Масштабирование растровых изображенийОдним из недостатков растровой графики является так называемая пикселизация изображений при их увеличении (если не приняты специальные меры). Раз в оригинале присутствует определенное количество точек, то при большем масштабе увеличивается и их размер, становятся заметны элементы растра, что искажает саму иллюстрацию. Для противодействия пикселизации принято заранее оцифровывать оригинал с разрешением, достаточным для качественной визуализации при масштабировании.Другой прием состоит в применении стохастического растра, позволяющего уменьшить эффект пикселизации в определенных пределах. Наконец, при масштабировании используют метод интерполяции, когда увеличение размера иллюстрации происходит не за счет масштабирования точек, а путем добавления необходимого числа промежуточных точек.Иногда характеристики растрового изображения записывают в такой форме: 1024x768x24. Это означает, что ширина изображения равна 1024 пикселям, высота — 768 и глубина цвета равна 24. 1024x768 — рабочее разрешение для 15 — 17 дюймовых мониторов. Несложно догадаться, что размер несжатого изображения с такими параметрами будет равен 1024*768*24 = 18874368 байт. Это более 18 мегабайт — слишком много для одной картинки, особенно если требуется хранить несколько тысяч таких картинок — это не так уж много по компьютерным меркам. Вот почему компьютерную графику используют почти всегда в сжатом виде.

Сжатие растровой графикиRLE (Run Length Encoding) — метод сжатия, заключающийся в поиске последовательностей одинаковых пикселей в сточках растрового изображения («красный, красный, ..., красный» записывается как «N красных»).LZW (Lempel—Ziv—Welch) — более сложный метод, ищет повторяющиеся фразы — одинаковые последовательности пикселей разного цвета. Каждой фразе ставится в соответствие некоторый код, при расшифровке файла код замещается исходной фразой.При сжатии файлов формата JPEG (с потерей качества) изображение разбивается на участки 8x8 пикселей, и в каждом участке их значение усредняется. Усреднённое значение располагается в левом верхнем углу блока, остальное место занимается меньшими по яркости пикселями. Затем большинство пикселей обнуляются. При расшифровке нулевые пиксели получают одинаковый цвет. Затем к изображению применяется алгоритм Хаффмана.Сжатие применяется и для векторной графики, но здесь уже нет таких простых закономерностей, так как форматы векторных файлов достаточно сильно различаются по содержанию.

Достоинства: Недостатки:

1Растровая графика эффективно представляет реальные образы. Реальный мир состоит из миллиардов мельчайших объектов и человеческий глаз как раз приспособлен для восприятия огромного набора дискретных элементов, образующих предметы. На своем высшем уровне качества — изображение выглядят вполне реально подобно тому, как выглядят фотографии в сравнении с рисунками. Это верно только для очень детализированных изображений, обычно получаемых сканированием фотографий. Помимо естественного вида растровые изображения имеют другие преимущества. Устройства вывода, такие как лазерные принтеры, для создания изображений используют наборы точек. Растровые изображения могут быть очень легко распечатаны на таких принтерах, потому что компьютерам легко управлять устройством вывода для представления отдельных пикселов с помощью точек

2Растровые изображения занимают большое количество памяти. Существует так же проблема редактирования растровых изображений, так как большие растровые изображения занимают значительные массивы памяти, то для обеспечения работы функций редактирования таких изображений потребляются так же значительные массивы памяти и другие ресурсы компьютера.
Тема 3

Растровый графический редактор — специализированная программа, предназначенная для создания и обработки растровых изображений. Подобные программные продукты нашли широкое применение в работе художников-иллюстраторов, при подготовке изображений к печати типографским способом или на фотобумаге, публикации в интернете.

Растровые графические редакторы позволяют пользователю рисовать и редактировать изображения на экране компьютера, а также сохранять их в различных растровых форматах, таких как, например, JPEG и TIFF, позволяющих хранить растровую графику с незначительным снижением качества за счёт использования алгоритмов сжатия с потерями, PNG и GIF, поддерживающими хорошее сжатие без потерь, и BMP, также поддерживающем сжатие (RLE), но в общем случае представляющем собой несжатое «попиксельное» описание изображения.

В противоположность векторным редакторам, растровые используют для представления изображений матрицу окрашенных точек (bit map). Однако, большинство современных растровых редакторов содержат векторные инструменты редактирования в качестве вспомогательных

Существует также такое понятие как коэффициент прямоугольности пикселов. В отличие от коэффициента прямоугольности изображения он относится к реальным размерам видео пиксела и является отношением реальной ширины к реальной высоте. Данный коэффициент зависит от размера дисплея и текущего разрешения, и поэтому на разных компьютерных системах принимает различные значения. Цвет любого пиксела растрового изображения запоминается в компьютере с помощью комбинации битов. Чем больше битов для этого используется, тем больше оттенков цветов можно получить. Число битов, используемых компьютером для любого пиксела, называется битовой глубиной пиксела. Наиболее простое растровое изображение состоит из пикселов имеющих только два возможных цвета черный и белый, и поэтому изображения, состоящие из пикселов этого вида, называются однобитовыми изображениями. Число доступных цветов или градаций серого цвета равно 2 в степени равной количеству битов в пикселе.

Цвета, описываемые 24 битами, обеспечивают более 16 миллионов доступных цветов и их часто называют естественными цветами. Растровые изображения обладают множеством характеристик, которые должны быть организованы и фиксированы компьютером.

Размеры изображения и расположение пикселов в нем это две основных характеристики, которые файл растровых изображений должен сохранить, чтобы создать картинку. Даже если испорчена информация о цвете любого пиксела и любых других характеристиках компьютер все равно сможет воссоздать версию рисунка, если будет знать, как расположены все его пикселы. Пиксел сам по себе не обладает никаким размером, он всего лишь область памяти компьютера, хранящая информацию о цвете, поэтому коэффициент прямоугольности изображения не соответствует никакой реальной размерности. Зная только коэффициент прямоугольности изображения с некоторой разрешающей способностью можно определить настоящие размеры рисунка. Поскольку размеры изображения хранятся отдельно, пикселы запоминаются один за другим, как обычный блок данных. Компьютеру не приходится сохранять отдельные позиции, он всего лишь создает сетку по размерам заданным коэффициентом прямоугольности изображения, а затем заполняет ее пиксел за пикселом.

Размер растра обычно измеряется количеством пикселов по горизонтали и вертикали. Можно сказать, что для компьютерной графики зачастую наиболее удобен растр с одинаковым шагом для обеих осей, то есть dpiХ = dpiУ. Это удобно для многих алгоритмов вывода графических объектов. Иначе — проблемы. Например, при рисовании окружности на экране дисплея EGA (устаревшая модель компьютерной видеосистемы, ее растр— прямоугольный, пикселы растянуты по высоте, поэтому для изображения окружности необходимо генерировать эллипс). Форма пикселов растра определяется особенностями устройства графического вывода (рис. 1.2). Например, пикселы могут иметь форму прямоугольника или квадрата, которые по размерам равны шагу растра (дисплей на жидких кристаллах); пикселы круглой формы, которые по размерам могут и не равняться шагу растра (принтеры). Для экранной копии достаточно разрешения 72 dpi, для распечатки на цветном или лазерном принтере 150—200 dpi, для вывода на фотоэкспонирующем устройстве 200—300 dpi. Установлено эмпирическое правило, что при распечатке величина разрешения оригинала должна быть в 1,5 раза больше, чем линиатура растра устройства вывода. В случае, если твердая копия будет увеличена по сравнению с оригиналом, эти величины следует умножить на коэффициент масштабирования

Разрешение оригинала. Разрешение оригинала измеряется в точках на дюйм (dots per inch — dpi) и зависит от требований к качеству изображения и размеру файла, способу оцифровки и создания исходной иллюстрации, избранному формату файла и другим параметрам. В общем случае действует правило: чем выше требование к качеству, тем выше должно быть разрешение оригинала.

Разрешение экранного изображения. Для экранных копий изображения элементарную точку растра принято называть пикселом. Размер пиксела варьируется в зависимости от выбранного экранного разрешения (из диапазона стандартных значений), разрешение оригинала и масштаб отображения

. Мониторы для обработки изображений с диагональю 20—21 дюйм (профессионального класса), как правило, обеспечивают стандартные экранные разрешения 640х480, 800х600, 1024х768,1280х1024,1600х1200,1600х1280, 1920х1200, 1920х1600 точек. Расстояние между соседними точками люминофора у качественного монитора составляет 0,22—0,25 мм.(+ тетрадь)

Разрешение печатного изображения и понятие линиатуры. Размер точки растрового изображения как на твердой копии (бумага, пленка и т. д.), так и на экране зависит от примененного метода и параметров растрирования оригинала. При растрировании на оригинал как бы накладывается сетка линий, ячейки которой образуют элемент растра. Частота сетки растра измеряется числом линий на дюйм (lines per inch — Ipi) и называется линиатурой.

Размер точки растра рассчитывается для каждого элемента и зависит от интенсивности тона в данной ячейке. Чем больше интенсивность, тем плотнее заполняется элемент растраДля абсолютно белого цвета значение заполняемости составит 0%. На практике заполняемость элемента на отпечатке обычно составляет от 3 до 98

Таким образом, разрешающая способность характеризует расстояние между соседними пикселами (рис. 1.). Разрешающую способность измеряют количеством пикселов на единицу длины. Наиболее популярной единицей измерения является dpi (dots per inch) — количество пикселов в одном дюйме длины (2.54 см). Не следует отождествлять шаг с размерами пикселов — размер пикселов может быть равен шагу, а может быть как меньше, так и больше, чем шаг.
Тема 15

Диаграмма— это графически представленная зависимость одной величины от другой. С помощью диаграмм взаимосвязь между данными становится более наглядной. Диаграммы облегчают сравнение различных данных. Большинство диаграмм упорядочивают данные по горизонтальной (ось категорий) и вертикальной осям (ось значений). Отдельные элементы данных называются точками. Несколько точек образуют последовательность данных.

Элементы диаграммы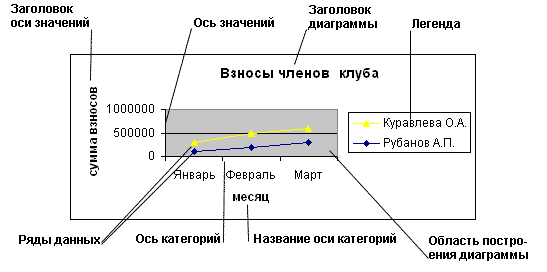

http://detc.usu.ru/assets/acomp0021/images/41a.gif

Мастер диаграмм.

Хорошим помощником в построении диаграмм является мастер диаграмм. Он выполняет основную часть работы. Все что остается делать Вам - выбирать данные и принимать по ходу некоторые несложные решения. Покажем работу мастера на примере построения диаграммы распределения воды и суши на земном шаре. Выделите диапазон значений, которые предполагается изобразить на диаграмме и щелкните на кнопке

Chart Wizard (Мастер диаграмм) или выберите команду Chart (Диаграмма) из меню Insert (Вставка). Появится окно первого шага мастера диаграмм.

На первом шаге необходимо выбрать тип диаграммы. Выберите объемный вариант круговой диаграммы и щелкните на кнопке Next (Далее) для того, чтобы перейти ко второму шагу.
На втором шаге уточняется диапазон данных. В нашем примере нужный диапазон уже определен, но в случае необходимости его можно изменить, выделив с помощью «протаскивания» новый диапазон. В результате в строке Data range (Диапазон) появится соответствующая ссылка. Кликните на кнопке Next (Далее) для того, чтобы перейти к третьему шагу.
На третьем шаге определяются отображаемые элементы диаграммы. Наш мастер диаграмм предложил первую ячейку столбца значений в качестве заголовка диаграммы, а содержимое первого столбца диапазона включил в легенду. Если бы Вы выбрали другой тип диаграммы, мастер предложил бы Вам другие решения. Если Вы не согласны с мастером, Вы можете внести свои поправки на этом шаге. Хорошая диаграмма — это диаграмма, при просмотре которой не возникает вопрос: «А что бы это значило?». Для этого ее надо снабдить достаточным количеством понятных подписей. Щелкните на кнопке Next (Далее) для того, чтобы перейти к последнему шагу.
4 На четвертом шаге необходимо указать размещение диаграммы. По умолчанию мастер предлагает разместить диаграмму на том же рабочем листе, на котором находятся данные. Этот параметр тоже можно изменить. Щелкните на кнопке Finish (Готово) для завершения работы мастера диаграмм.

Типы диаграмм

(Гистограммы). Гистограммы удобно использовать для представления элементов, которые сравниваются в пределах одного временного периода, или для иллюстрации изменений, происходящих с разными элементами в пределах нескольких периодов. Их можно также использовать для сравнения годовых показателей реализации продукции за последние несколько лет. Таким же образом можно представить расходы, а затем сравнить между собой реализацию и расходы на протяжении определенного периода времени.Bar (Линейчатые) диаграммы — это те же гистограммы, но с иной ориентацией осей. В отличие от гистограмм здесь ось х (или ось категорий) расположена вертикально, а ось у (или ось значений) — горизонтально. Линейчатые диаграммы применяются в тех же случаях, что и гистограммы. Горизонтальное расположение оси зависимых переменных делает их особенно удобными для сравнительного представления разных величин в пределах одного временного периода. Скажем, реализацию товара за месяц различными продавцами лучше всего продемонстрирует линейчатая диаграмма.Line (Графики) используются для того, чтобы показать развитие процесса во времени или по категориям. Причем, по оси категорий всегда откладываются равные интервалы, поэтому графики используются для отображения изменений, происходящих через регулярные отрезки времени (например, дни, недели или месяцы.Pie (Круговые) диаграммы демонстрируют соотношение между целым и его частями. На них лучше всего видно, какую часть целого составляет тот или иной его компонент (например, весь бюджет и отдельные его статьи, весь инвестиционный портфель и входящие в него инвестиции). Принцип построения круговой диаграммы следующий: сначала суммируются все данные из выделенного диапазона, а затем определяется, какую часть этого целого составляет содержимое каждой ячейки. Некоторые типы круговых диаграмм позволяют выделить одну или несколько частей целого.Doughnut (Кольцевые) диаграммы - это одна из разновидностей круговых диаграмм. Они также демонстрируют соотношение частей в целом. Но у них есть одно существенное отличие: на кольцевых диаграммах, в отличие от круговых, можно представлять разные данные.Radar (Лепестковые) диаграммы едва ли могут быть удобны в использовании, за исключением каких-то очень специальных случаев. Они демонстрируют соотношения между разными последовательностями данных, а также между каждой последовательностью и всеми последовательностями одновременно. В результате все оказывается свалено в одну кучу, и получить четкое представление о сути представляемого предмета обычно весьма проблематично. Лепестковые диаграммы иногда используют в задачах административного управления сложными проектами.XY Scatter (Точечные) диаграммы широко используются в статистике. Их достоинство в том, что они могут иллюстрировать степень связности элементов данных (представленных точками), а также степень близости элементов данных со средним значением. На точечных диаграммах отображают изменения данных, происходящие за некоторый промежуток времени. Это роднит их с графиками. В чем же специфика использования точечных диаграмм? В графиках по оси категорий всегда откладаваются равные интервалы, тогда как на точечных диаграммах можно представлять данные, для которых интервалы времени имеют разную величину.. Объемные диаграммы выглядят несколько сложнее, но используются они практически в тех же случаях, что и плоские. В семействе объемных диаграмм обособленно стоят Surface (Поверхностные)диаграммы. Их используют для демонстрации взаимосвязи нескольких переменных или для наглядного представления больших объемов данных, которые иначе трудно интерпретировать. Такая диаграмма выглядит как рельефная географическая карта, показывая «возвышенности» и «впадины» для большой совокупности данных.

Нет Диаграммы с областями. Пузырьковая диаграмма. Биржевая диаграмма. Комбинированая диаграмма.

Тема 9

Фрактальная графика, как и векторная вычисляемая, но отличается тем, что никакие объекты в памяти не хранятся. Изображение строится по уравнению, или системе уравнений, поэтому ничего кроме формулы хранить не надо. Изменив коэффициенты можно получить совершенно другую картину. Фрактальными свойствами обладают многие объекты живой и неживой природы (снежинка, ветка папоротника). Способность фрактальной графики моделировать образы вычислительным путем часто используют для автоматической генерации необычных иллюстраций, поверхности местности.

Фрактал(лат. fractus — дробленый) — термин, означающий геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком. В более широком смысле под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, строго большую топологической.Следует отметить, что слово «фрактал» не является математическим термином и не имеет общепринятого строгого математического определения. Оно может употребляться, когда рассматриваемая фигура обладает какими-либо из перечисленных ниже свойств:

Обладает нетривиальной структурой на всех шкалах. В этом отличие от регулярных фигур (таких, как окружность, эллипс, график гладкой функции): если мы рассмотрим небольшой фрагмент регулярной фигуры в очень крупном масштабе, он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, на всех шкалах мы увидим одинаково сложную картину.

Является самоподобной или приближённо самоподобной.

Обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую.

Может быть построена при помощи рекурсивной процедуры.

Многие объекты в природе обладают фрактальными свойствами, например побережья, облака, кроны деревьев, кровеносная система и система альвеол человека или животных.Фракталы, особенно на плоскости, популярны благодаря сочетанию красоты с простотой построения при помощи компьютера.Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке (например, множество Кантора). Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы».

Литература Среди литературных произведений находят такие, которые обладают текстуальной, структурной или семантической фрактальной природой. В текстуальных фракталах потенциально бесконечно повторяются элементы текста

неразветвляющееся бесконечное дерево, тождественные самим себе с любой итерации («У попа была собака…», «Притча о философе, которому снится, что он бабочка, которой снится, что она философ, которому снится…», «Ложно утверждение, что истинно утверждение, что ложно утверждение…»)
неразветвляющиеся бесконечные тексты с вариациями («У Пегги был весёлый гусь…») и тексты с наращениями («Дом, который построил Джек»)

В структурных фракталах схема текста потенциально фрактальна

венок сонетов (15 стихотворений), венок венков сонетов (211 стихотворений), венок венков венков сонетов (2455 стихотворений)
«рассказы в рассказе» («Книга тысячи и одной ночи», Я.Потоцкий «Рукопись, найденная в Сарагоссе»)
предисловия, скрывающие авторство (У.Эко «Имя розы»)
Т.Стоппард «Розенкранц и Гильденстерн мертвы» (сцена с представлением перед королём)

В семантических и нарративных фракталах автор рассказывает о бесконечном подобии части целому

Х. Л. Борхес «В кругу развалин»
Х.Кортасар «Жёлтый цветок»
Ж.Перек «Кунсткамера»

Рекурсивная процедура получения фрактальных кривых

Существует простая рекурсивная процедура получения фрактальных кривых на плоскости. Зададим произвольную ломаную с конечным числом звеньев, называемую генератором. Далее, заменим в ней каждый отрезок генератором (точнее, ломаной, подобной генератору). В получившейся ломаной вновь заменим каждый отрезок генератором. Продолжая до бесконечности, в пределе получим фрактальную кривую. На рисунке справа приведены три первых шага этой процедуры для кривой Коха.

множество Кантора — нигде не плотное несчётное совершенное множество. Модифицировав процедуру, можно также получить нигде не плотное множество положительной длины.

треугольник Серпинского и ковёр Серпинского — аналоги множества Кантора на плоскости.

кривая Коха — несамопересекающаяся непрерывная кривая бесконечной длины, не имеющая касательной ни в одной точке;

кривая Пеано — непрерывная кривая, проходящая через все точки квадрата.

траектория броуновской частицы также с вероятностью 1 нигде не дифференцируема. Её хаусдорфова размерность равна двум.

Тема 10

губка Менгера — аналог множества Кантора в трёхмерном пространстве;

Начиная с конца XIX века, в математике появляются примеры самоподобных объектов с патологическими с точки зрения классического анализа свойствами. К ним можно отнести следующие:Примерами таких кривых служат:кривая дракона;кривая Коха;кривая Леви;кривая Минковского, кривая Пеано.с помощью похожей процедуры получается дерево Пифагора.

Мно́жество Мандельбро́та — это множество, таких точек c на комплексной плоскости, для которых итеративная последовательность z₀=0, z_n=z_n_-1²+c (n=1, 2, 3, …) не уходит на бесконечность. То есть, это множество таких c, для которых существует действительное R, что неравенство |z_n|<R выполняется при всех натуральных n.Множество Мандельброта является в некотором смысле фракталом. Его фрагменты не строго подобны исходному множеству, но при многократном увеличении определённые части всё больше похожи друг на друга.

Лампочка Мандельброта — трёхмерный фрактал, аналог множества Мандельброта, созданный Дэниелом Уайтом и Полом Ниландером с использованием гиперкомплесной алгебры основанной на сферических координатах. Назван в честь создателя фрактальной геометрии Бенуа Мандельброта. Формула для n-ой степени трехмерного гиперкомплексного числа $\langle x, y, z\rangle$ таков $\langle x, y, z\rangle^n = r^n\langle\cos(n\theta)\cos(n\phi),\sin(n\theta)\cos(n\phi),\sin(n\phi)\rangle$ а:

Мальдебертовы облака-какая то нарисованная с помощью фракталов, очень красивая….
Тема 11

Фракталы в комплексной динамике. Множество Жюлиа́.Фракталы естественным образом возникают при изучении нелинейных динамических систем. Наиболее изучен случай, когда динамическая система задаётся итерациями многочлена или голоморфной функции комплексной переменной на плоскости. Первые исследования в этой области относятся к началу XX века и связаны с именами Фату и Жюлиа.Пусть F(z) — многочлен, z₀ — комплексное число и рассмотрим следующую последовательность:

$z_0, z_1=f(z_0), z_2=f(z_1), z_3=f(z_2), \dots$ .

Нас интересует поведение этой последовательности при $n\rightarrow\infty$ . Эта последовательность может:

Стремиться к бесконечности;
Стремиться к конечному пределу;
Демонстрировать в пределе циклическое поведение, то есть поведение вида $\dots w_1, w_2, w_3, w_1, w_2, w_3,\dots$
Демонстрировать более сложное поведение.

Множества значений z₀, для которых последовательность демонстрирует один конкретный тип поведения, а также множества точек бифуркации между различными типами, часто обладают фрактальными свойствами.

Так, множество Жюлиа на картинке справа — множество точек бифуркации для многочлена F(z) = z² + c, то есть тех значений z₀, для которых поведение последовательности z_n может резко меняться при сколь угодно малых изменениях z₀.

множество Мандельброта — это множество всех $c\in\mathbb{c}$ , при которых z_n для F(z) = z² + c и z₀ = 0 не стремится к бесконечности.

Ещё один известный пример такого рода — бассейны Ньютона.

Бассе́йны Нью́тона, фракталы Ньютона — разновидность алгебраических фракталов.

Области с фрактальными границами появляются при приближенном нахождении корней нелинейного уравнения алгоритмом Ньютона на комплексной плоскости (для функции действительной переменной метод Ньютона часто называют методом касательных, который, в данном случае, обобщается для комплексной плоскости). ^[1]

Применим метод Ньютона для нахождения нуля функции комплексного переменного, используя процедуру:

$z_{n+1}=z_n-\frac{f(z_n)}{f\'(z_n)}.\!$

Выбор начального приближения $z_0\!$ представляет особый интерес. Т.к. функция может иметь несколько нулей, в различных случаях метод может сходиться к различным значениям. Однако, что за области обеспечат сходимость к тому или иному корню?

для дополнения множества Мандельброта можно раскрасить точки в зависимости от скорости стремления z_n к бесконечности (определяемой, скажем, как наименьший номер n, при котором | z_n | превысит фиксированную большую величину A).

Примеры стохастических фракталов Природные объекты часто имеют фрактальную форму. Для их моделирования могут применяться стохастические (случайные) фракталы.:

траектория броуновского движения на плоскости и в пространстве;
граница траектории броуновского движения на плоскости. В 2001 году Лоулер, Шрамм и Вернер доказали предположение Мандельборта о том, что её размерность равна 4/3.
эволюции Шрамма-Лёвнера — конформно-инвариантные фрактальные кривые, возникающие в критических двумерных моделях статистической механики, например в модели Изинга и перколяции.
различные виды рандомизированных фракталов, то есть фракталов, полученных с помощью рекурсивной процедуры, в которую на каждом шаге введён случайный параметр. Плазма — пример использования такого фрактала в компьютерной графике.

Фрактальная монотипия, или стохатипия — направления в изобразительном искусстве, состоящие в получении изображения случайного фрактала.

Биоморфы — фракталы, построенные на основе комплексной динамики и напоминающие живые организмы.

Примеры фракталов в природе. – снежинка, водоросли и тд

Применение фракталов

Компьютерная графика

Фракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких, как деревья, кусты, горные ландшафты, поверхности морей и так далее

Анализ рынков

Последнее время Фракталы стали популярны у «трейдеров» для анализа курса фондовых бирж, валютных и торговых рынков.

Физика и другие естественные науки

В физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких, как турбулентное течение жидкости, сложные процессы диффузии-адсорбции, пламя, облака и т. п. Также фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).

Фрактальные антенны

Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который тогда жил в центре Бостона, где была запрещена установка на зданиях внешних антенн. Натан вырезал из алюминиевой фольги фигуру в форме кривой Коха и наклеил её на лист бумаги, а затем присоединил к приёмнику. Оказалось, что такая антенна работает не хуже обычной. И хотя физические принципы работы такой антенны не изучены до сих пор, это не помешало Коэну основать собственную компанию и наладить их серийный выпуск.

Сжатие изображений

Существуют алгоритмы для сжатия изображения с помощью фракталов. Они основаны на идее о том, что вместо изображения можно хранить отображение сжатия, для которого это изображение является неподвижной точкой.

Децентрализованные сети

Система назначения IP-адресов в сети Netsukuku хранит всего 4 Кб информации о состоянии соседних узлов, при этом любой новый узел подключается к общей сети без необходимости в центральном регулировании раздачи IP-адресов, что, например, характерно для сети Интернет. Таким образом, принцип фрактального сжатия информации гарантирует полностью децентрализованную, а следовательно, максимально устойчивую работу всей сети.