Приближенные методы решения алгебраических и трансцендентных уравнений
 Скачать 89.03 Kb. Скачать 89.03 Kb.
|
|
Санкт-Петербургский политехнический университет Петра Великого Институт металлургии, машиностроения и транспорта Кафедра компьютерных технологий в машиностроении Отчёт по лабораторной работе № 4 Дисциплина: Вычислительная математика Тема: Приближенные методы решения алгебраических и трансцендентных уравнений Студент гр. 23335/1 Стрекозов А.В. Преподаватель Ситкин Д.С. « »________2017г. Цель работы - изучение численных методов решения алгебраических и трансцендентных уравнений. Задание Найти все корни уравнения с точностью до пяти знаков. Для одного из корней проделать ручные расчеты трех шагов приближений. Методы нахождения корней:
Найти также все корни уравнения с помощью встроенной функции MathCAD root.
Пусть уравнение имеет вид f(x)=0. Функция f(x)определена в некотором конечном или бесконечном интервале a≤x≤b . Всякое значение x* обращающее функцию f(x) в нуль называется корнем уравнения. При отыскании приближенных значений корней уравнения приходится решать две задачи: - Отделение корней. Отыскиваются ограниченные области, в каждой из которых заключен один и только один корень уравнения. - Вычисление корней с заданной точностью. График функции f(x), ее первой f’(x) и второй производной f’’(x), а также уточнение границ интервалов [ai ,bi] представлены на рисунке 1. 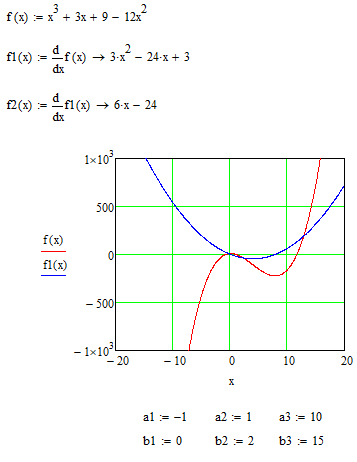 Рисунок 1 Нахождение корней методом деления отрезка пополам представлено на рисунке 2. 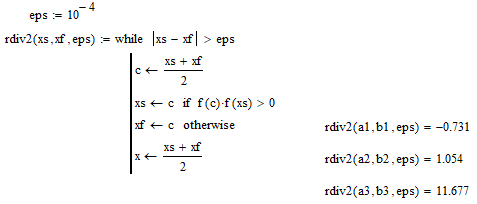 Рисунок 2 Нахождение корней методом хорд представлено на рисунке 3. 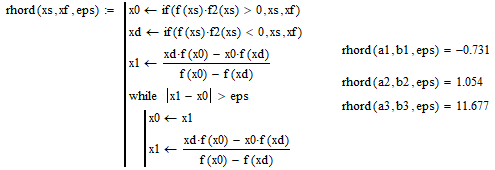 Рисунок 3 Нахождение корней методом касательных представлено на рисунке 4. 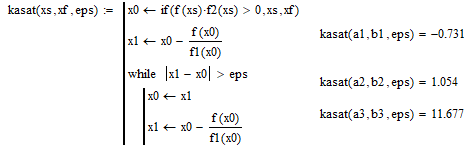 Рисунок 4 Нахождение корней методом интераций представлено на рисунке 5.  Рисунок 5 Проверка результатов с помощью встроенной функции root представлена на рисунок 6. 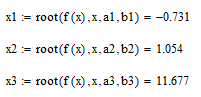 Рисунок 6 Вывод: были изучены приемы отделения корней и численные методы приближенного решения алгебраических и трансцендентных уравнений. |
