Лабораторная работа №46. изучение явления интерференции и дифрак. Приборы и принадлежности
 Скачать 183.5 Kb.
|
|
Цель работы: изучение явления интерференции в толстой стеклянной плас- тине и дифракции на микрообъектах с использованием лазера; определение показателя преломления стекла и размеров щели (толщины нити). Приборы и принадлежности: гелий - неоновый лазер с электрическим блоком питания ; оптическая скамья , на которой расположены : рейтер с объекти- вом и экраном 1, рейтер с дифракционным объектом 2(раздвижной щелью или нитью), рейтер с толстой плоскопараллельной стек- лянной пластиной 3, экран 4 , измеритель- ная линейка (рис.1).                          В работе источником света является лазер. Излучение лазера отличается сле-дующими свойствами: помимо значительной мощности и малой угловой рас-ходимости светового пучка , он обладает высокой степенью монохроматичнос-ти - большой длиной когерентности. Длина когерентности - наибольшее рас- стояние вдоль направления распространения волны, на котором колебания мож-но считать когерентными между собой. I) Изучение интерференции света при отражении от толстой стеклянной пластины. Высокая степень монохроматичности излучения лазера позволяет наблюдать интерференцию световых волн при очень большой разности хода, возникающей возникающей в толстой плоскопараллельной стеклянной пластине. Расходя- щийся световой пучок (рис.1.), полученный от лазера с помощью объектива О (фокус этого объектива совпадает с плоскостью экранаЭ), падает на пластину П. Отраженные от передней и задней поверхностей пластины П световые волны интерферируют между собой и дают на экране Э систему концентрических светлых и темных колец (рис.2).                                  На (рис.2)  - радиус к - го темного кольца на экране, d - толщина пластины,l - расстояние между экраном и пластиной. В наших опытах << l и α << l.Используя условие появления интерференционных минимумов при отражении света в тонкой пластине:  , где к = 1,2,3,… - порядок интер-ференции, α - угол падения лучей, n - показатель преломления стеклянной плас-тины, λ - длина волны света, и приближенную формулу  ,получим  , откуда: Так как << l, то  Подставляя это значение в (1), получим Из формулы (2) видно, что  линейно зависит от порядка интерференции К. Это означает, что линейно зависит и от номеров колец N. Поэтому если пост-роить график зависимости от N, то по тангенсу угла наклона этого графика: можно найти: Данная формула позволяет графическим методом определить коэффициент пре-ломления стеклянной пластины. Таблица1: [ r ] = мм. 
Построив график и определив тангенс угла наклона прямой β, получаем значе- ние 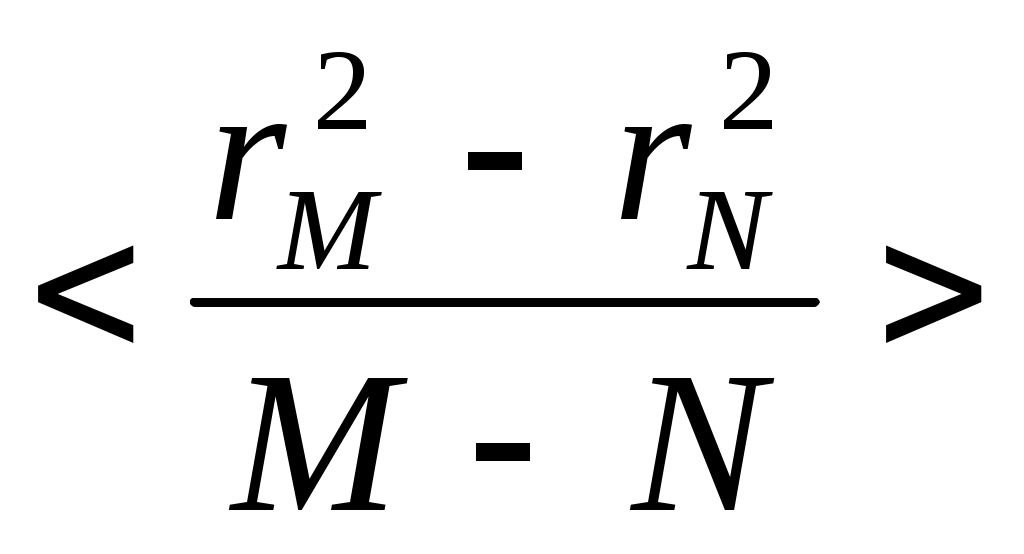 : 57.04  .По формуле (3) рассчитаем n: n = (20 * 10^-3 * 57.04 * 10^-6) / (4*0.166*0.6328*10^-6) = = 1140.8*10^-9/0.42*10^-6 = 2.7 Т.е.
Определим максимальный порядок интерференции:  . 2*2.7*20*10^-3/0.6328*10^-6 = 170 * 10^3 II) Изучениедифракции от щели и нити. Е                         сли на пути лазерного пучка поставить щель, то на экране за щелью будет наб-людаться дифракционная картина в виде центрального (наиболее яркого мак-симума ) и системы симметричных относительно него максимумов различных порядков, разделенных минимумами. (рис.3).     На установке наблюдаемые углы дифракции  , и, как показывает расчет,минимумы возникают в тех направлениях, для которых угол  удовлетворяет условию:  , где b - ширина щели, - угол , соот-ветствующий минимуму к - того порядка. В данном случае  так как  Здесь - расстояние от центра дифракционной картины до минимума к - того порядка, l - расстояние между щелью и экраном. Поэтому формула (5) представима в виде  Откуда можно найти ширину диф-ракционной полосы  или ширину щели: Теперь рассмотрим дифракцию от нити. Согласно теореме Бабине дифракци- онные картины от препятствия и от равного ему отверстия должны быть совер-шенно одинаковы вне области свободного ( прямого ) пучка. Следовательно, дифракционная картина от нити (вне области прямого пучка ) будет такой же, как и от щели, ширина которой равна толщине нити, и для расчета дифракции от нити можно воспользоваться той же формулой (6), что и для щели. Таблица2:
Рассчитаем ширину щели: b = 0.6328 *10^-6 * 47*10^-2 / 3*10^-3 = 10^-4 м δb = 0.00005/0.6328 + 0.5/47 + 0.5/3 = 0.18 Δb = 0.18 * 10^-4м Т.е.
Аналогичны расчеты для нити: b = 0.6328 *10^-6 * 47*10^-2 / 2*10^-3 = 1.50 * 10^-4 м δb = 0.00005/0.6328 + 0.5/47 + 0.5/2 = 0.25 Δb = 0.39 * 10^-4м Т.е.
Вывод: в ходе проделанной работы были изучены устройства и принцип дейст- вия лазера, что позволило использовать данную установку в ходе экспе- римента по изучению интерференции в толстой стеклянной пластине и и дифракции на микрообъектах. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
