VARAKIN_Поиск и синхронизация ШПСcorr. Прием информаций и неопределенность во времени и по частоте в широкополосных системах связи
 Скачать 244.26 Kb. Скачать 244.26 Kb.
|
|
17.2. Сравнение непрерывного и дискретного поиска ШПС по времени В гл. 15, 16 и в § 17.1 приведено достаточно много различных формул, определяющих поиск и синхронизацию ШПС по времени. Эти формулы получены для различных, на первый взгляд, условий. Поэтому необходимо дать сравнение этих условий и ределить основные факторы, определяющие поиск и синхронизацию ШПС по времени. Дисперсии ошибки измерения времени многоканальным оптимальным измерителем определяется формулой (15.25). Эта формула выражает потенциальную помехоустойчивость, при этом дисперсия (15.25) минимальна для заданного отношения сигнал-шум Многоканальный измеритель является дискретным измерителем, так как весь диапазон изменения времени разделяется на конечное число интервалов неопределенности, равное числу каналов. Схема АПВ реализует непрерывный поиск. Точность измерения времени в АПВ характеризуется двумя составляющими с дисперсией шума фильтрации и с дисперсией шумовой составляющей Прежде всего отметим, что поскольку отношение Это действительно имеет место в реальных ШСС, так как должно быть а отношение Поэтому в дальнейшем шумы фильтрации не рассматриваются. Для сравнения дисперсий (15.25) и (17.7) необходимо сначала выразить в (15.25) через реальный параметр ФМ - ШПС длительность одиночного импульса . АКФ ФМШПС не имеет второй производной Для приближенного решения задачи заменим центральный пик параболой: при При этом Подставляя это значение в (15.21), находим Заменяя в согласно найденному соотношению, где энергия накапливаемых ШПС, N — спектральная плотность шума, получаем энергия ШПС, обрабатываемого когерентно. Положим, что длительность ШПС равна Т, а число накапливаемых ШПС равно Поэтому из (17.12) Сравнивая (17.7) с (17.13), находим, что схема АПВ обеспечивает потенциальную помехоустойчивость, если ее шумовая полоса Из (17.14) следует, что шумовая полоса обратно пропорциональна длительности ШПС, обрабатываемого когерентно. Поскольку шумовая полоса связана с параметрами ФНЧ (17.5), то, зная заданную помехоустойчивость измерителя (17.13), можно однозначно найти параметры фильтра АПВ. Число накапливаемых можно найти из следующих соображений. Вероятность ошибки при приеме дискретной информации при рассинхронизации определяется формулой (15.34). Положим, что вероятность ошибки при приеме ФМ ШПС увеличивается на 15% из-за рассинхронизации, т. е. При этом отношение сигнал-помеха на выходе измерительного канала (накопителя) и отношение сигнал-помеха на выходе информационного канала соотносятся следующим образом: Так как то при когерентном накоплении в соответствии с (17.15) число накапливаемых ШПС Из (17.14) находим, что шумовая полоса АПВ должна быть равна Время поиска ШПС в АПВ ограничивается скоростью перестройки (17.11). В формуле (17.11) первая производная является безразмерной величиной. За длительность ШПС, равную Т, интервал времени, проходимый схемой поиска, равен Соответственно время поиска Рисунок 17.6 иллюстрирует определение времени анализа одной ячейки неопределенности длительностью в схеме АПВ. Так как согласно то Таким образом, чем больше скорость перестройки, тем меньше время анализа одной ячейки и тем меньше время поиска ШПС. Вместе с тем, необходимо помнить, что скорость перестройки ограничена согласно (17.11). Если в (17.18) подставить значение согласно (17.14), то Так как число импульсов в то т. е. время поиска пропорционально числу накапливаемых ШПС, базе (или числу импульсов) и длительности ШПС. В ряде случаев интерес представляет относительное время поиска Из (17.20) имеем Если число накапливаемых согласно (17.16), то Обратимся теперь к дискретному поиску, при котором время задержки опорного ШПС изменяется дискретно. Ранее было допущено, что число параметров по времени задержки согласно (15.35) и где Эти соотношения свидетельствуют, что шаг перестройки схемы поиска 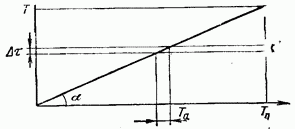 Рис. 17.6. Время анализа ячейки неопределенности Если число символов в , то общее число шагов перестройки Если взять число накапливаемых импульсов равным то время поиска т. е. совпадает со временем поиска схемой При имеем соотношения (17.22). Таким образом, доказано, что схемы поиска с непрерывным и дискретным изменением задержки опорного ШПС обладают одинаковыми характеристиками поиска. При этом необходимо иметь в виду основное соотношение (17.14), связывающее шумовую полосу с длительностью ШПС, обрабатываемого когерентно, и равной где число накапливаемых ШПС в когерентном накопителе. При сравнении не были учтены переходной процесс в ложные срабатывания АПВ (ложные тревоги) и пропуск ШПС. Если допустить для простоты, что ложных тревог и пропусков ШПС нет, то ко времени поиска (17.18) — (17.22) надо добавить время переходного процесса Тпер (17.10), которое и является временем вхождения в синхронизм . Положим, что Согласно Суммируя время поиска (17.20) и длительность переходного процесса , находим время синхронизации Если то со временем переходного процесса можно не считаться. При этом время синхронизма практически совпадает со временем поиска ШПС. Такой вывод справедлив при условии, что вероятности ложных тревог и пропуска ШПС малы. При увеличении вероятности ложных тревог схема АПВ будет останавливаться на каждом ложном выбросе и задерживаться до окончания переходного процесса В этом случае учет длительности переходного процесса необходим. Вероятности ложных тревог и пропуска ШПС будут малыми только в том случае, если на выходе измерительного канала (или на выходе схемы АПВ) отношение сигнал-помеха будет существенно больше единицы. 17.3. Алгоритмы поиска ШПС по времени задержки Непрерывный поиск ШПС по времени задержки, осуществляемый схемой АПВ, реализует так называемый последовательный поиск, когда интервал неопределенности последовательно просматривается схемой поиска до обнаружения ШПС и вхождения в синхронизм. Если осуществляется дискретный поиск ШПС по времени задержки, то последовательно просматриваются все ячейки неопределенности с шагом Такой поиск называется последовательным шаговым поиском. Последовательный поиск (в том числе и шаговый) называется иногда слепым поиском. Как следует из материалов данного раздела, основными характеристиками процесса поиска ШПС является вероятность правильного обнаружения ШПС с оценкой его параметров и время поиска. При оптимизации процедуры поиска возможны два критерия: 1. критерий минимума среднего времени поиска при заданной вероятности обнаружения; 2. критерий максимума вероятности обнаружения при заданном времени поиска. Как было отмечено ранее, наряду с последовательным поиском может осуществляться и параллельный поиск. Последовательный поиск осуществляется схемой АПВ, параллельный поиск — многоканальным измерителем, в котором число каналов равно числу ячеек неопределенности. Время поиска максимально при последовательном поиске и минимально при параллельном поиске, но многоканальный измеритель значительно сложнее схемы АПВ. Следует отметить, что многоканальный измеритель в ШСС необходим только в процессе поиска ШПС и вхождения в синхронизм. Во время приема информации при измеренных (и уже известных) параметрах ШПС надо иметь только коррелятор. На рис. 17.7 изображена упрощенная схема квазиоптимального приемника ШСС. Синхронизатор (С) осуществляет поиск ШПС и синхронизацию генератора ШПС (ГШПС). Информация выделяется с помощью коррелятора (К) и решающего устройства (РУ). Обычно задача разработчика ШСС заключается в том, чтобы обеспечить минимальное время поиска ШПС при минимальной сложности синхронизатора, причем полагают вероятностные характеристики обнаружения и измерения заданными. Такая задача до настоящего времени не имеет окончательного решения. Известно большое число различных вариантов построения синхронизаторов и процедур поиска [6, 7, 8, 13, 15, 16, 96—99, 105]. Кроме последовательного (одноканального) и параллельного (многоканального) поиска на практике используются параллельно-последовательный, многоэтапный, полихотомический поиск ШПС по времени. Кроме того, известны алгоритмы поиска с учетом алгебраических свойств ФМ ШПС и беспоисковый алгоритм [105]. Кратко рассмотрим отмеченные алгоритмы с учетом вероятностных характеристик обнаружения ШПС. 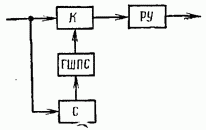 Рис. 17.7. Квазноптимальный приемник ШСС Последовательный поиск. Положим, что имеется ячеек неопределенности, а центральный пик АКФ ШПС расположен в последней ячейке. Процесс поиска останавливается каждый раз, когда возникает ложная тревога, а завершается правильным обнаружением ШПС. Обозначим через среднюю длительность цикла поиска до ложной тревоги, а через среднее число циклов до завершения поиска. В этом случае среднее значение времени поиска [97] Более точно формула (17.24) определяет среднее значение максимального времени поиска, так как было предположено, что полезный сигнал содержится в последней ячейке неопределенности. Известно [97], что среднее значение времени поиска (17.24) 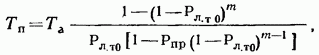 где — время анализа одной ячейки, вероятность ложной тревоги ячейке (15.43), где нет полезного сигнала, вероятность пропуска полезного сигнала [формулы (15.45) при При этом процедура поиска может закончиться правильным обнаружением с вероятностью 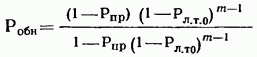 или ложной тревогой с вероятностью 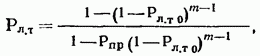 причем Допустим, что отношение сигнал-помеха на выходе измерительного канала достаточно высоко, так что можно положить При этом из формул (17.26), (17.27) имеем а из Полагая где число символов в число накапливаемых ШПС, получаем что совпадает с временем поиска АПВ и одноканального измерителя, найденного ранее (17.20) без учета характеристик обнаружения. Если то но вероятность правильного обнаружения поиск закончится ложной тревогой. Если то из-за пропуска ШПС. Поэтому при заданных вероятностных характеристиках обнаружения можно найти среднее значение времени поиска. При конечных вероятностях среднее значение времени поиска будет всегда больше значения, определяемого согласно (17.20). При последовательном поиске с использованием последовательного анализа Вальда время анализа Та не фиксируется, а определяется достижением сигнала на выходе накопителя определенного порога. При таком методе поиска вероятности обнаружения и ложной тревоги определяются выражениями (17.26), (17.27). Среднее значение времени поиска определяется соотношением [97] 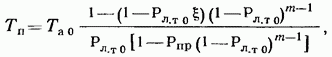 где время анализа в ячейке, где сигнала нет, — время анализа в ячейке, где есть сигнал. Если то (15.28) переходит в (17.25). Последовательно-параллельный поиск. При этом синхронизатор содержит I каналов, каждый из которых является одноканальным измерителем. Сначала синхронизатор анализирует ячеек неопределенности. Если сигнал не обнаружен, то синхронизатор перестраивается на I следующих ячеек. Эта процедура продолжается до тех пор, пока не произойдет обнаружение сигнала или постоянно будет фиксироваться ложная тревога. Число каналов в общем случае При имеем последовательный поиск, при параллельный поиск. При последовательно-параллельном поиске обычно отношение является целым числом. Среднее время поиска ШПС при последовательно-параллельном поиске [97] 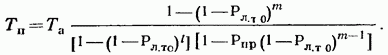 При малых вероятностях ошибок из (15.29) т. е. среднее значение времени поиска уменьшается в I раз. Чем больше каналов, тем меньше время поиска. При (последовательный поиск) время поиска при (параллельный поиск) Если вероятности ошибок конечны, то при формула (17.30) переходит в (17.25), а при (параллельный поиск) При использовании последовательного анализа Вальда имеем [97]: 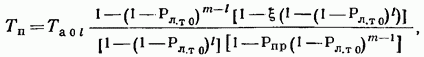 где среднее время анализа в группе из I ячеек, где сигнала нет: среднее время анализа в группе из I ячеек, среди которых сигнал есть. При формула (17.32) переходит в формулу (17.28). При формула (17.32) переходит в формулу (17.31) при условии, что Та — среднее значение времени анализа. Анализ времени поиска при последовательном, последовательно-параллельном и параллельном поиске показал, что при достаточно высоком отношении сигнал-помеха на выходе измерительного канала в первом приближении можно не учитывать вероятности ошибок и для оценки времени поиска целесообразно использовать простые формулы (17.20) и (17.30). Многоэтапный поиск. При многоэтапном поиске процесс поиска разбивают на несколько этапов. Результаты, полученные на предыдущем этапе, используют при анализе на последующем этапе. На первом этапе отмечают те ячейки, в которых произошло превышение порога, на втором этапе — анализируют только те, в которых ранее был превышен порог и т. д. При многоэтапном поиске возможно уменьшение времени поиска по следующим Причинам: во-первых, из-за уменьшения числа ячеек поиска на первом этапе при увеличении размера ячейки неопределенности; во-вторых, из-за уменьшения времени анализа ячейки при увеличении вероятности ложной тревоги на первых этапах: в-третьих, анализом на последующих этапах ограниченного числа ячеек, в которых наблюдалось превышение порога на первых этапах. При -этапном поиске вероятность правильного обнаружения [97] и вероятность ложной тревоги где вероятности пропуска ШПС и вероятность ложной тревоги на этапе. Для наиболее часто используемого двуэтапного поиска среднее значение времени поиска [97]: 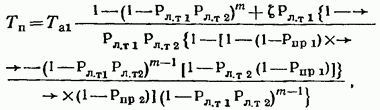 где вероятности ложной тревоги и пропуска сигнала на первом и втором этапах; среднее значение времени анализа на первом этапе; среднее значение времени анализа на втором этапе. При этом вероятность правильного обнаружения ШПС на втором (окончательном) этапе определяется формулой [97] 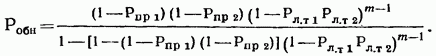 Среднее значение времени поиска (17.35) зависит от многих параметров. Можно оптимальным образом выбрать параметры первого и второго этапов, что позволяет, примерно, в 2 раза уменьшить время поиска по сравнению с одноэтапным последовательным поиском [97]. Увеличение числа этапов уменьшает время поиска, но уже при и 5 уменьшение времени поиска становится медленным и дальнейшее увеличение числа этапов нецелесообразно [97]. Полихотомический поиск. Разновидностью многоэтапного поиска является полихотомический поиск [96, 105]. При таком поиске область неопределенности делится на частей и с помощью специального синхронизатора определяется, в какой части находится ячейка с полезным сигналом. Затем часть области неопределенности, в которой содержится полезный сигнал, делится на частей и снова определяется часть, в которой содержится полезный сигнал и т. д. Эта процедура продолжается до тех пор, пока не будет определена единственная ячейка, в которой содержится полезный сигнал. Простейшим случаем полихотомического поиска является дихотомический поиск с при котором область неопределенности делится сначала на две части, затем также на две части и т. д. Для реализации полихотомии необходимо найти операцию деления области неопределенности на частей и определить структуру обнаружителя. 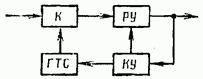 Рис. 17.8. Дихотомический обнаружитель В [96, 105] приведена схема обнаружителя, работающего по принципу дихотомии для поиска На рис. 17.8 приведена схема дихотомического обнаружителя. Коррелятор (К) последовательно вычисляет интегралов входного сигнала с тестовыми сигналами, снимаемых с генератора тестовых сигналов (ГТС). Смена тестовых сигналов производится командным устройством (КУ) после окончания интегрирования и принятия решения решающим устройством (РУ). Если полезный сигнал содержится в анализируемой части, то сигнал на выходе коррелятора максимален ртах, если полезного сигнала нет, то на выходе коррелятора сигнал будет обладать некоторым фоновым (взаимокорреляционным) значением Задача обнаружения сводится к распознаванию максимального значения на некотором фоне. Параметр где называется контрастностью ШПС. Для полихотомии найдено значение контрастности [105]: 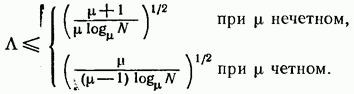 Соответственно при имеем Известно [105], что полихотомический поиск имеет определенные преимущества перед последовательным поиском: время поиска уменьшается в раз. Для дихотомии имеем выигрыш Вместе с тем, полихотомический поиск возможен только для специальных ШПС, построенных на основе функций Радемахера И Уолша [96, 105]. Поэтому полихотомические методы применимы в настоящее время только для очень ограниченного класса ШПС. Беспоисковая синхронизация. Так называют такой способ вхождения в синхронизм, при котором в состав синхронизатора на рис. 17.7 входит согласованный фильтр на весь ШПС или согласованный фильтр на некоторый сегмент ШПС с последующим накоплением (чаще всего с некогерентным накоплением). При этом синхронизатор не содержит генератора опорного ШПС с перестраиваемым временем задержки. Поскольку согласованный фильтр для ШПС с большой базой является очень сложным устройством и, кроме того, он необходим только в процессе поиска и вхождения в синхронизм, то обычно в синхронизаторе (рис. 17.7) используется согласованный фильтр, рассчитанный на обработку сегмента ШПС. Этот метод более детально будет рассмотрен в следующем параграфе. |
