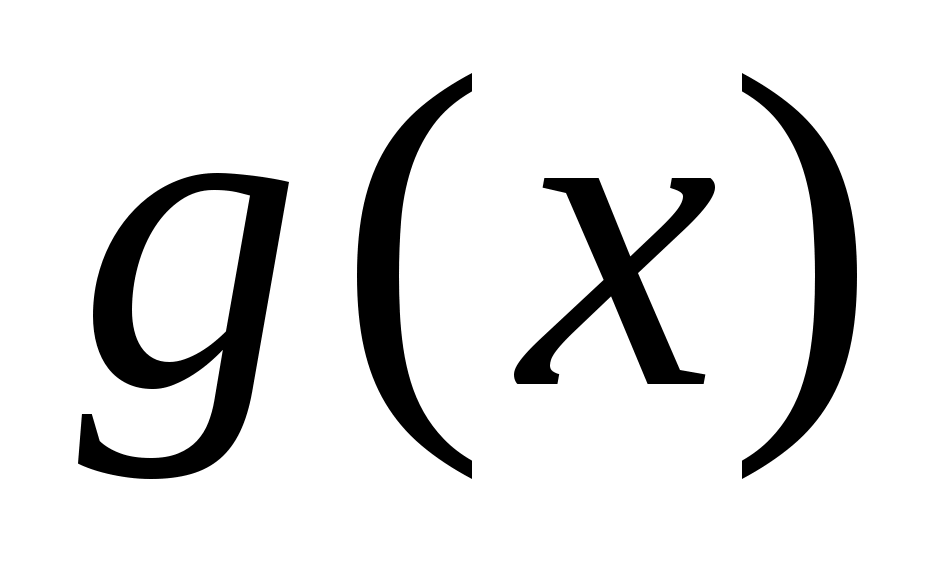 , определённый на шаге 2 алгоритма, будет собственным делителем многочлена , определённый на шаге 2 алгоритма, будет собственным делителем многочлена 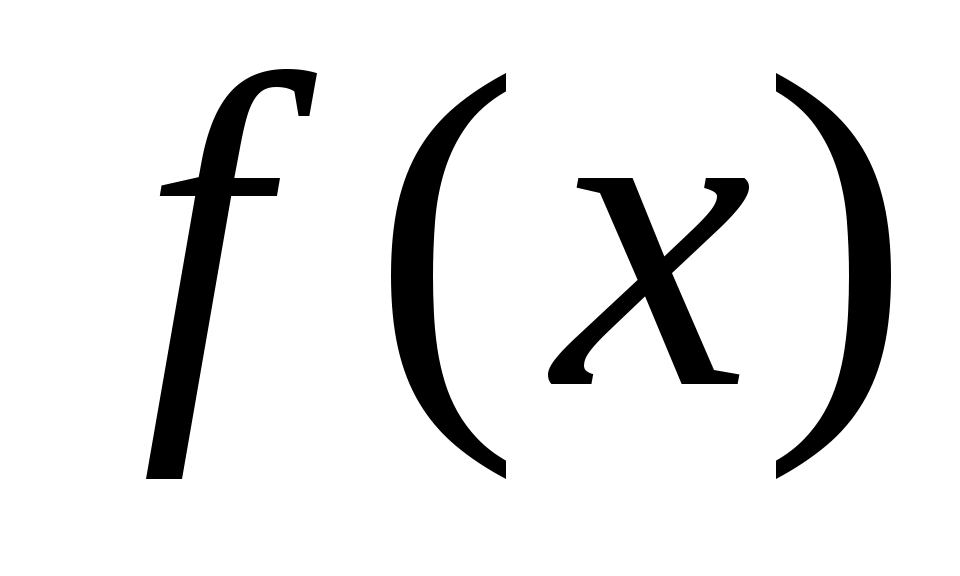 . .
Итак, существует не менее 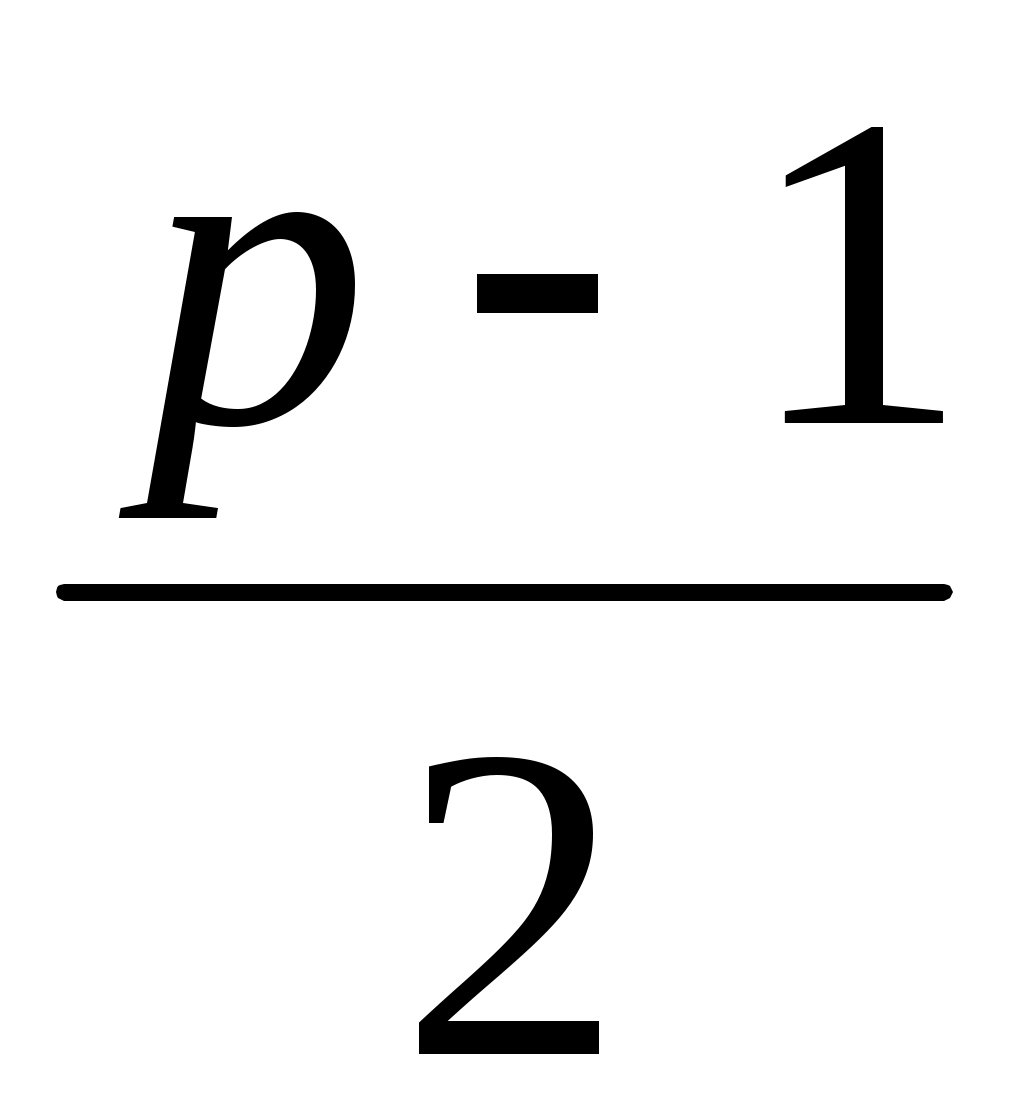 «удачных» выборов элемента «удачных» выборов элемента 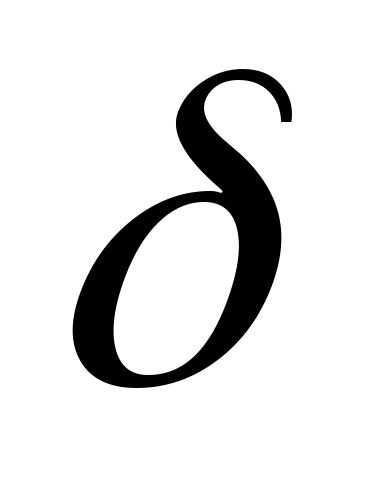 , при которых на шаге 2 алгоритма многочлен , при которых на шаге 2 алгоритма многочлен 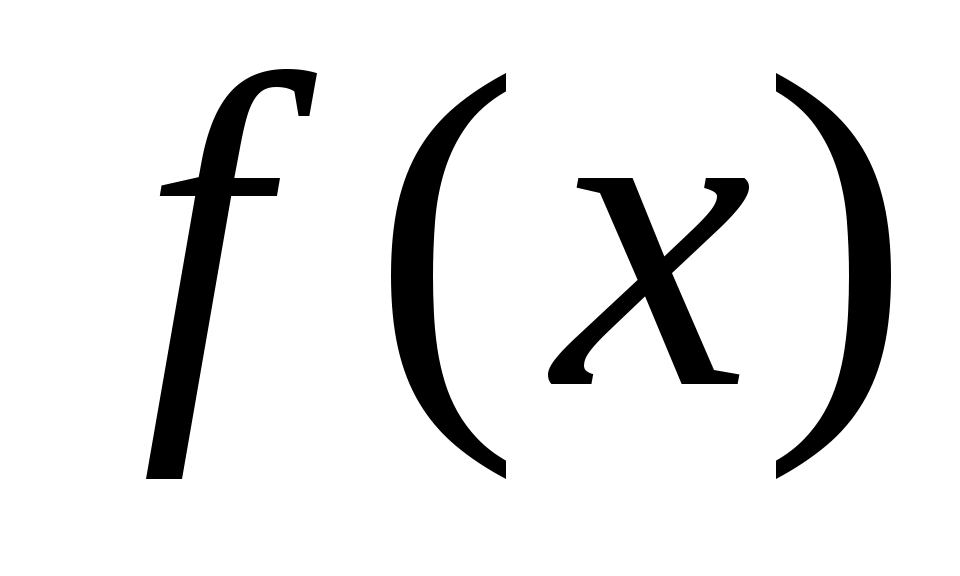 распадётся на два собственных множителя. Следовательно, при «случайном» выборе элемента распадётся на два собственных множителя. Следовательно, при «случайном» выборе элемента 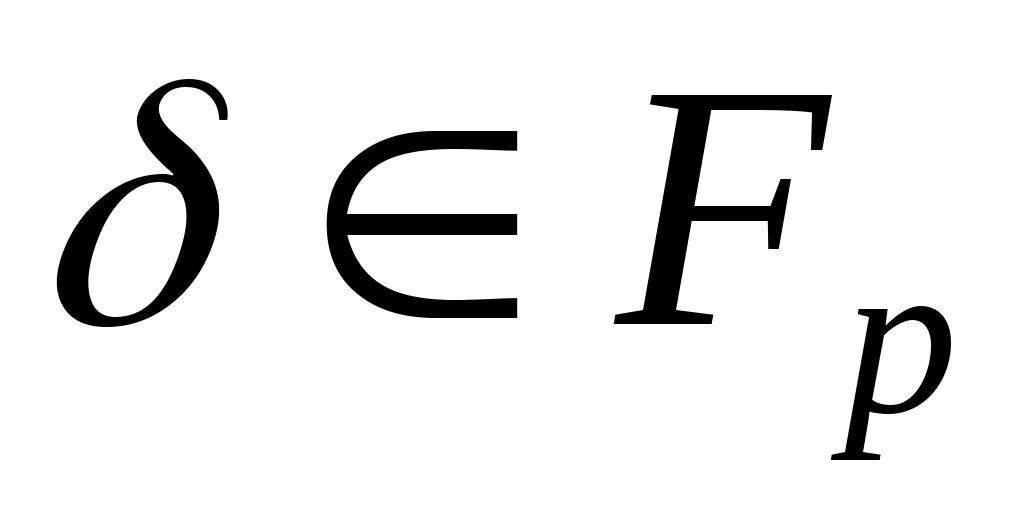 , вероятность того, что многочлен не разложится на множители после , вероятность того, что многочлен не разложится на множители после 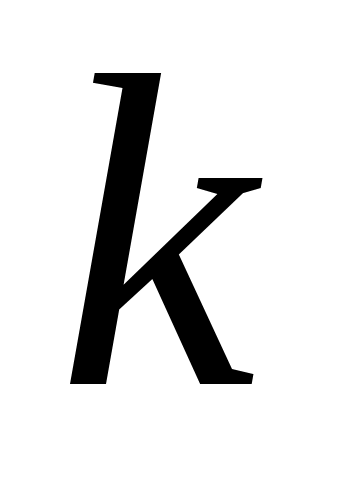 повторений шагов алгоритма 1-4. не превосходит повторений шагов алгоритма 1-4. не превосходит 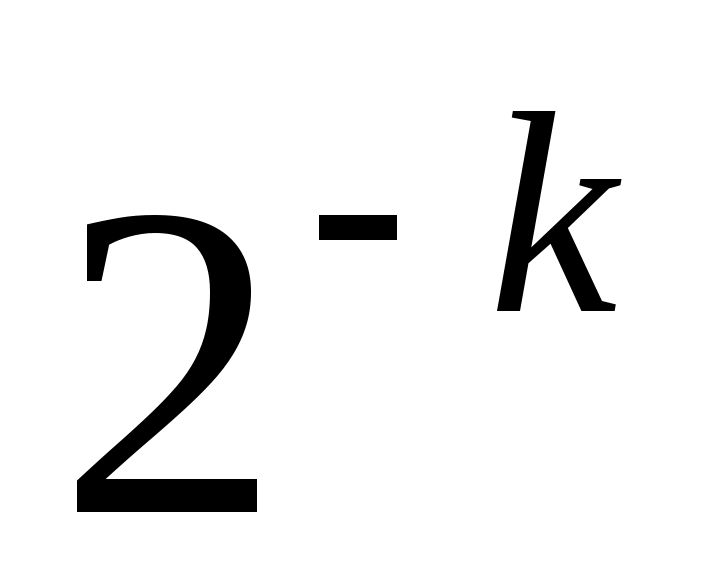 . Вероятность с ростом . Вероятность с ростом 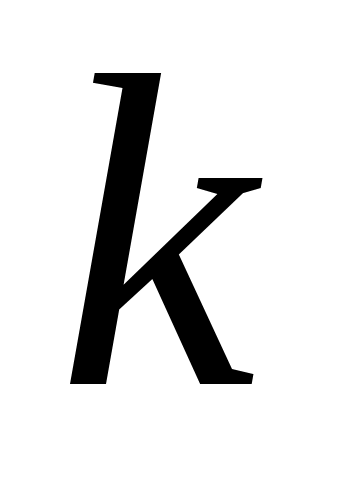 убывает очень быстро. И действительно, на практике этот алгоритм работает достаточно эффективно. убывает очень быстро. И действительно, на практике этот алгоритм работает достаточно эффективно.
Заметим, что при опенке вероятности мы использовали только два корня многочлена 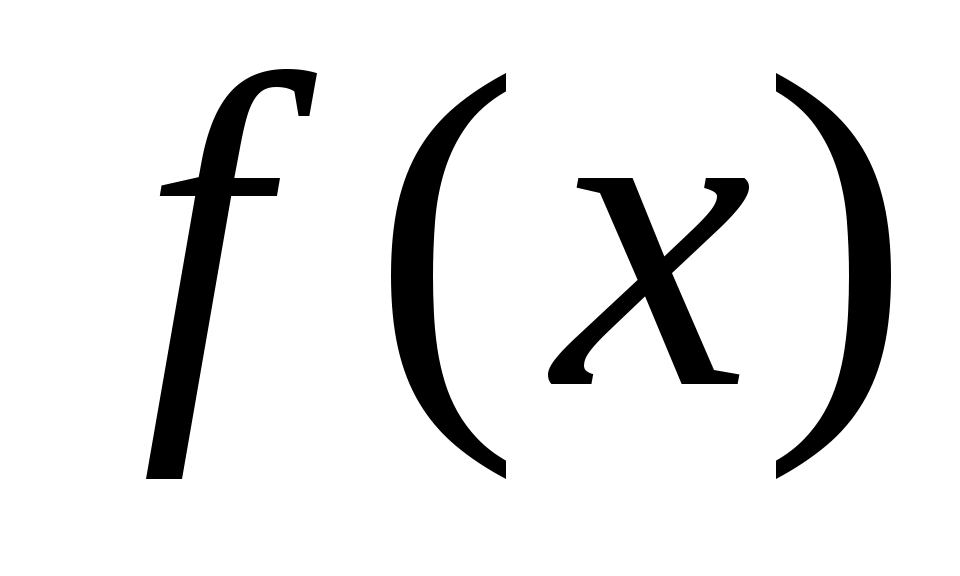 . При . При 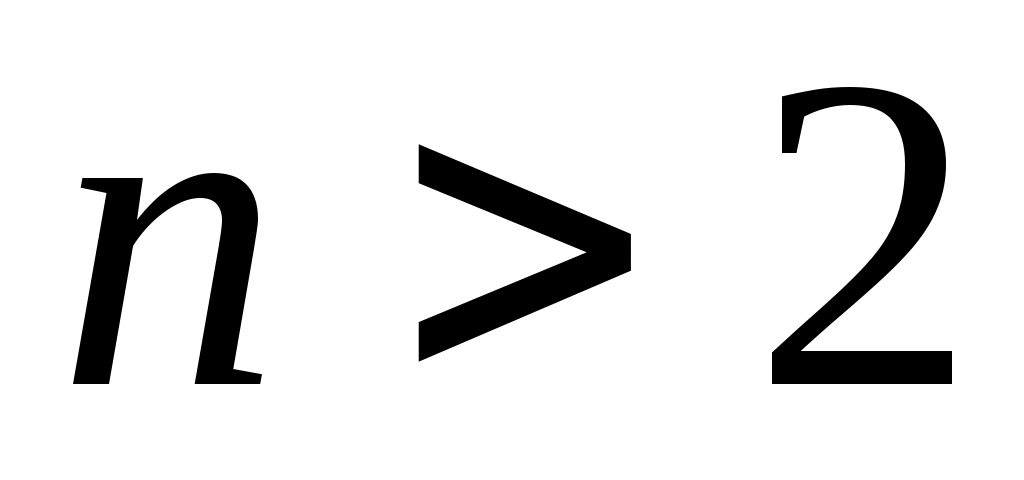 эта вероятность, конечно, еще меньше. Более тонкий анализ с использованием опенок А. Вейля для сумм характеров показывает, что вероятность для многочлена эта вероятность, конечно, еще меньше. Более тонкий анализ с использованием опенок А. Вейля для сумм характеров показывает, что вероятность для многочлена 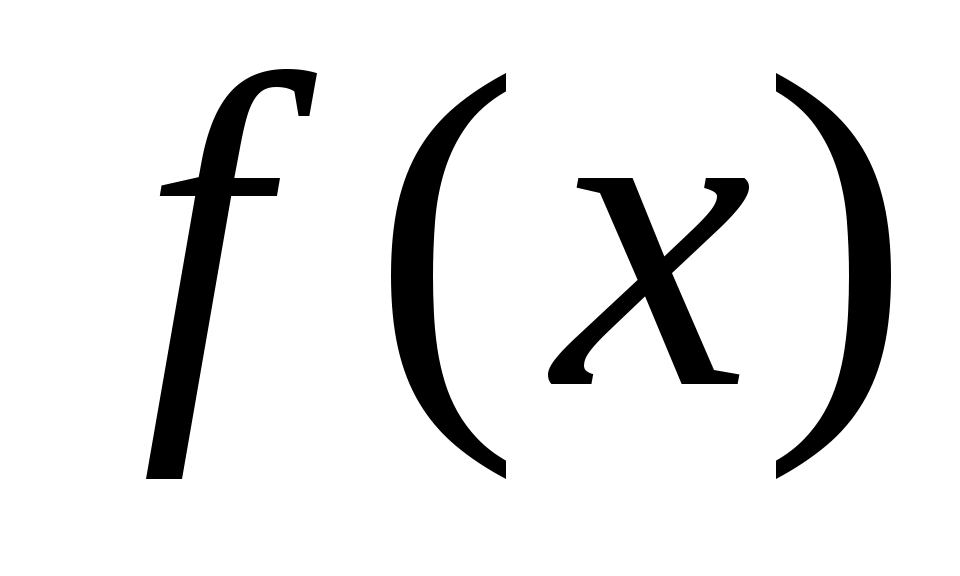 не распасться на множители при однократном проходе шагов алгоритма 1-4. не превосходит не распасться на множители при однократном проходе шагов алгоритма 1-4. не превосходит 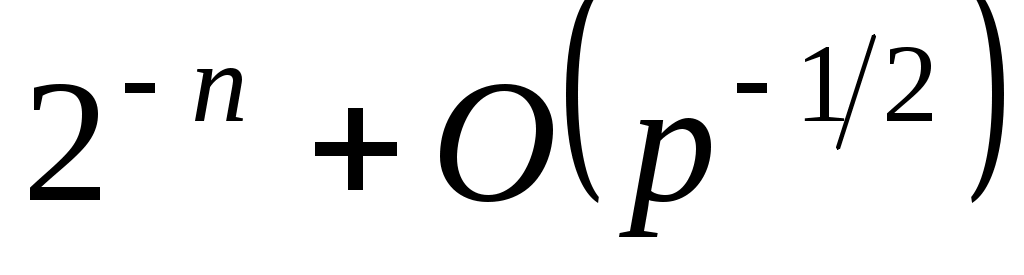 . Здесь постоянная в . Здесь постоянная в 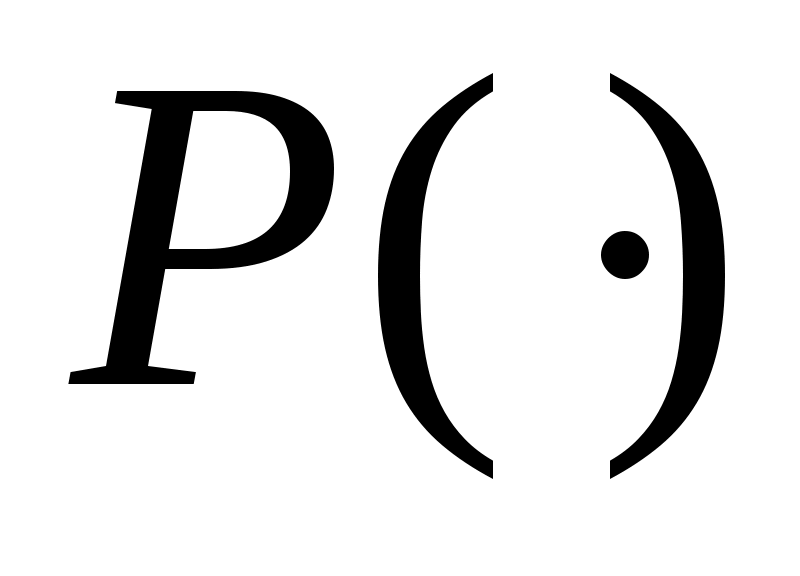 зависит от зависит от 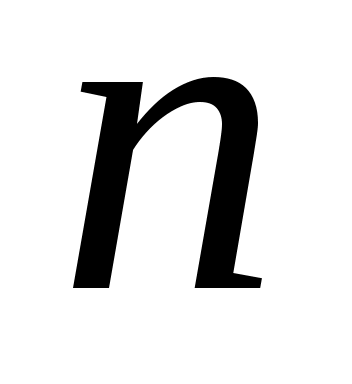 . .
Если в сравнении (8) заменить простой модуль 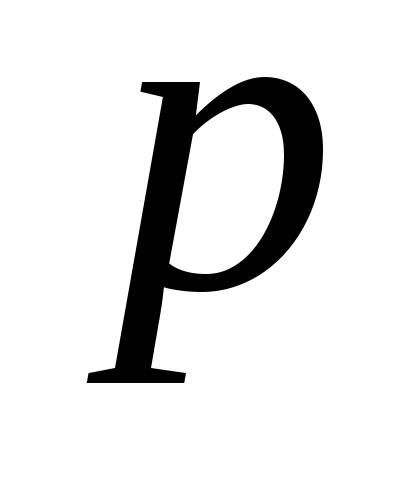 составным модулем составным модулем 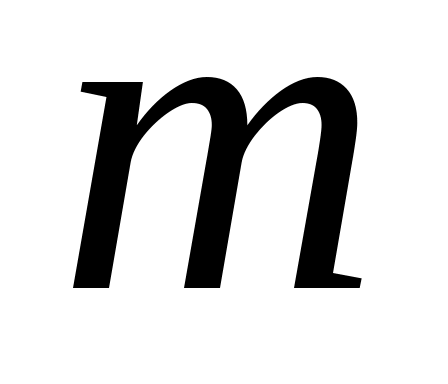 , то задача нахождения решений соответствующего сравнения становится намного более сложной. Известные алгоритмы её решения основаны на сведении сравнения к совокупности сравнений (8) по простым модулям — делителям , то задача нахождения решений соответствующего сравнения становится намного более сложной. Известные алгоритмы её решения основаны на сведении сравнения к совокупности сравнений (8) по простым модулям — делителям 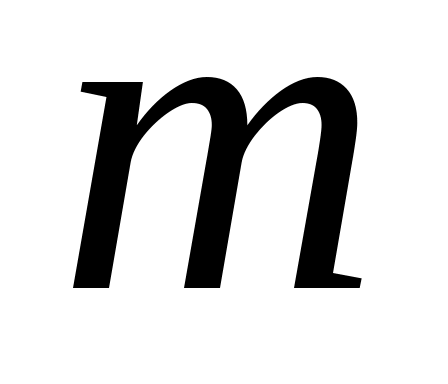 , и. следовательно, они требуют разложения числа то на простые сомножители, что, как уже указывалось, является достаточно трудоемкой задачей. , и. следовательно, они требуют разложения числа то на простые сомножители, что, как уже указывалось, является достаточно трудоемкой задачей.
3. КАЧЕСТВЕННАЯ ТЕОРИЯ АЛГОРИТМА RSA
Существует довольно эффективный способ убедиться, что заданное число является составным, не разлагая это число на множители. Согласно малой теореме Ферма, если число 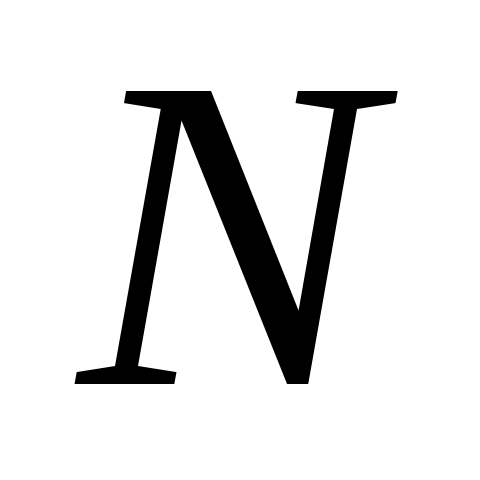 простое, то для любого целого простое, то для любого целого  , не делящегося на , не делящегося на 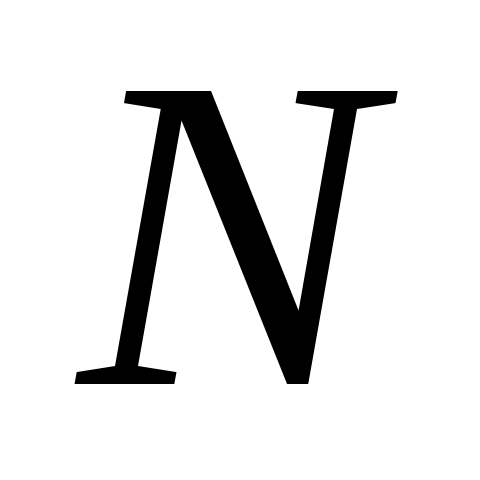 , выполняется сравнение , выполняется сравнение
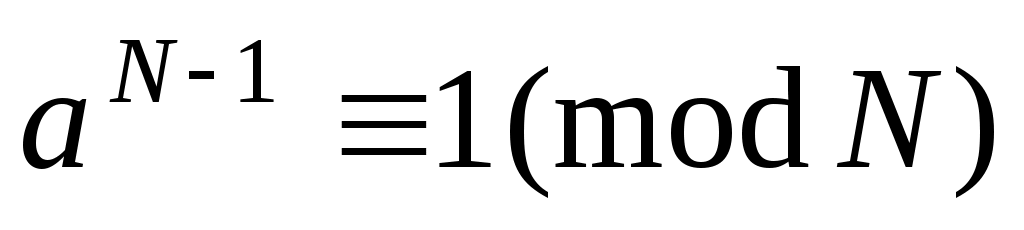 . (9) . (9)
Если же при каком-то  это сравнение нарушается, можно утверждать, что это сравнение нарушается, можно утверждать, что 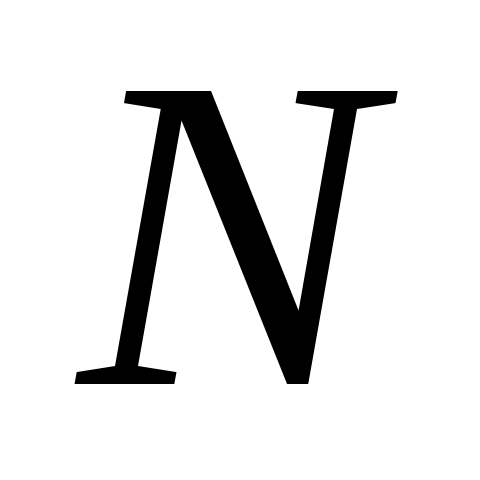 - составное. Проверка (9) не требует больших вычислений, это следует из алгоритма 1. Вопрос только в том, как найти для составного - составное. Проверка (9) не требует больших вычислений, это следует из алгоритма 1. Вопрос только в том, как найти для составного 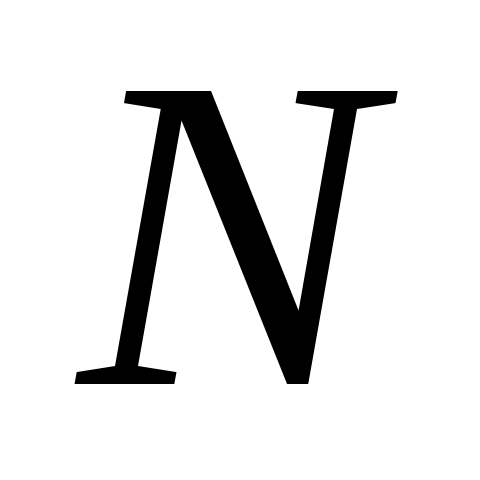 целое число целое число  , не удовлетворяющее (9). Можно, например, пытаться найти необходимое число , не удовлетворяющее (9). Можно, например, пытаться найти необходимое число  , испытывая все целые числа подряд, начиная с 2. Или попробовать выбирать эти числа случайным образом на отрезке , испытывая все целые числа подряд, начиная с 2. Или попробовать выбирать эти числа случайным образом на отрезке 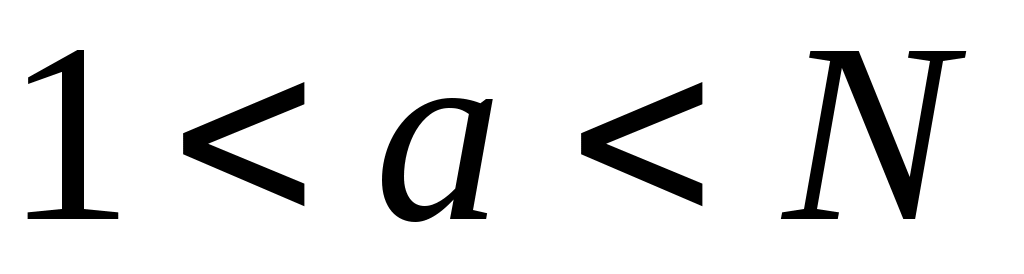 . .
К сожалению, такой подход не всегда даёт то, что хотелось бы. Имеются составные числа 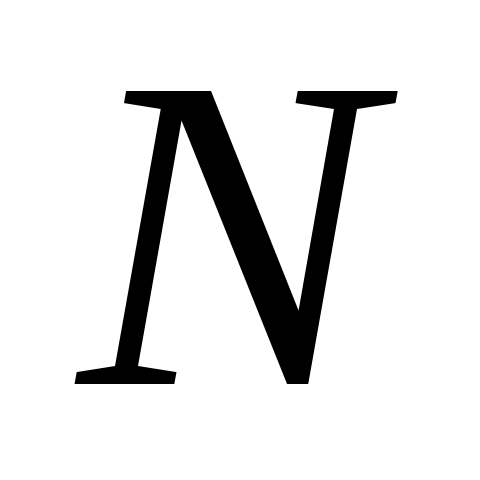 , обладающие свойством (9) для любого целого , обладающие свойством (9) для любого целого  с условием с условием 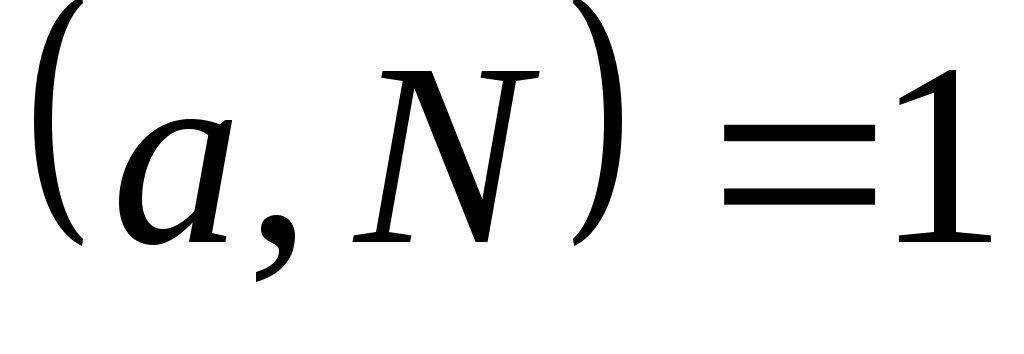 . Такие числа называются числами Кармайкла. Рассмотрим, например, число . Такие числа называются числами Кармайкла. Рассмотрим, например, число 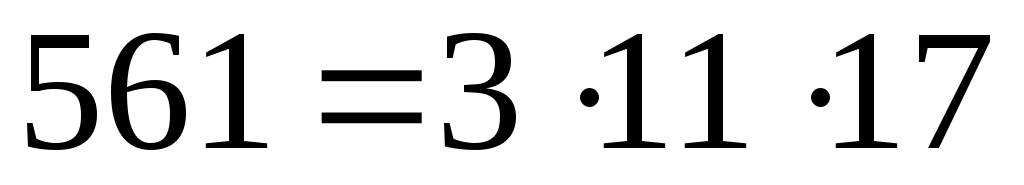 . Так как 560 делится на каждое из чисел 2, 10, 16, то с помощью малой теоремы Ферма легко проверить, что 561 есть число Кармайкла. Можно доказать, что любое из чисел Кармайкла имеет вид . Так как 560 делится на каждое из чисел 2, 10, 16, то с помощью малой теоремы Ферма легко проверить, что 561 есть число Кармайкла. Можно доказать, что любое из чисел Кармайкла имеет вид  , где все простые , где все простые 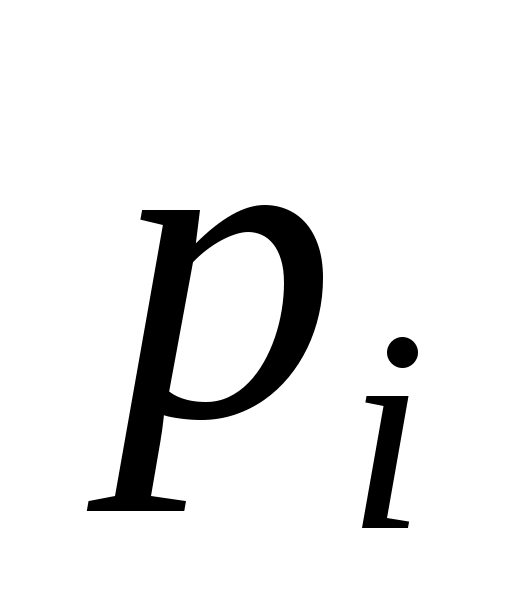 различны, причем различны, причем 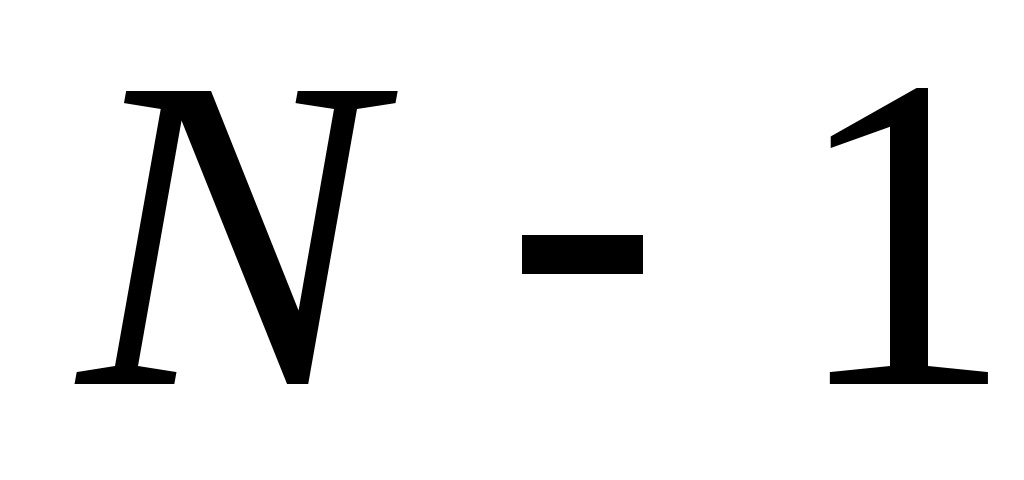 делится на каждую разность делится на каждую разность 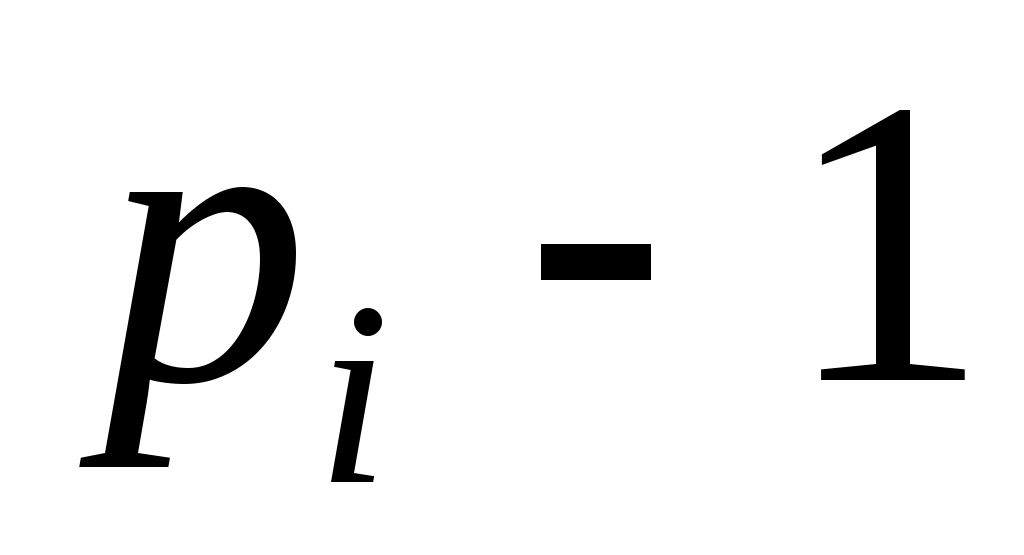 . Лишь недавно, была решена проблема о бесконечности множества таких чисел. . Лишь недавно, была решена проблема о бесконечности множества таких чисел.
В 1976 г. Миллер предложил заменить проверку (9) проверкой несколько иного условия. Если 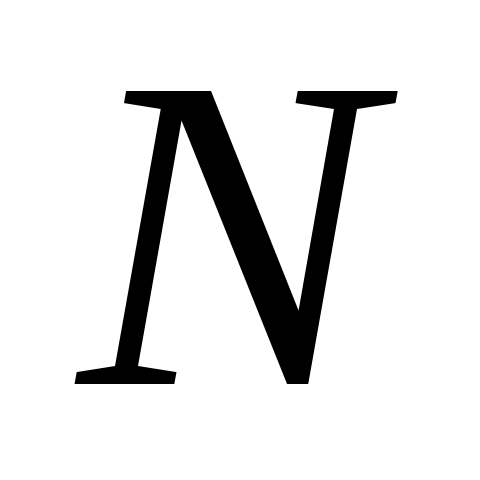 - простое число, - простое число, 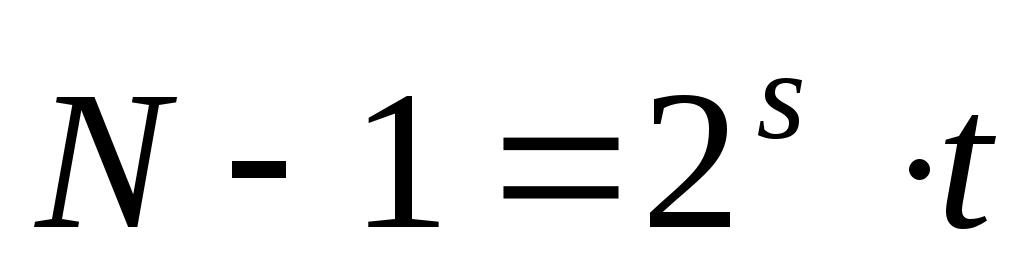 , где , где 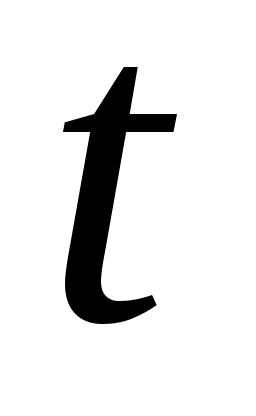 нечётно, то согласно малой теореме Ферма для каждого нечётно, то согласно малой теореме Ферма для каждого  с условием с условием 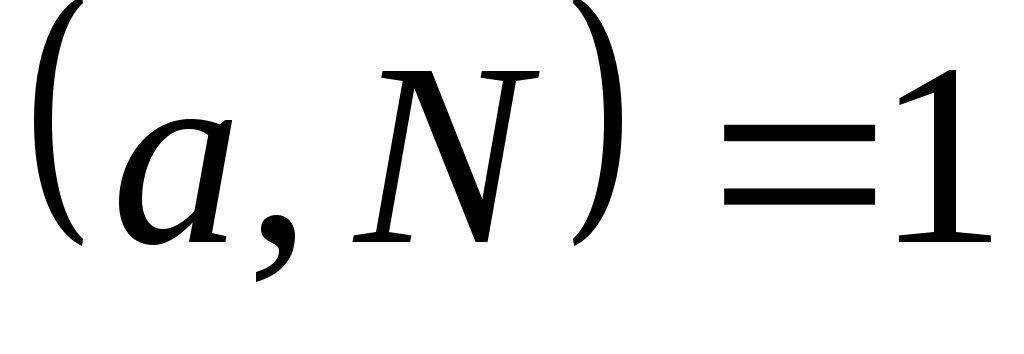 хотя бы одна из скобок в произведении хотя бы одна из скобок в произведении

делится на 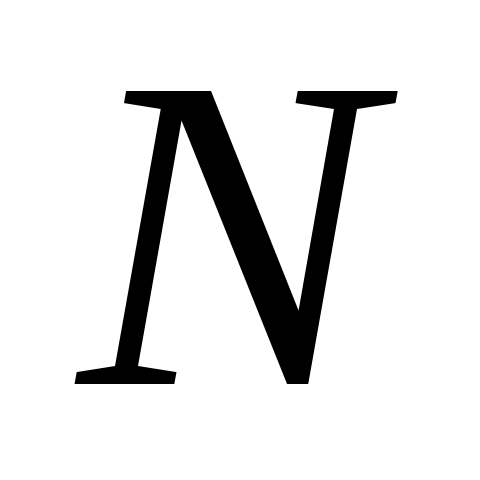 . Обращение этого свойства можно использовать, чтобы отличать составные числа от простых. . Обращение этого свойства можно использовать, чтобы отличать составные числа от простых.
Пусть 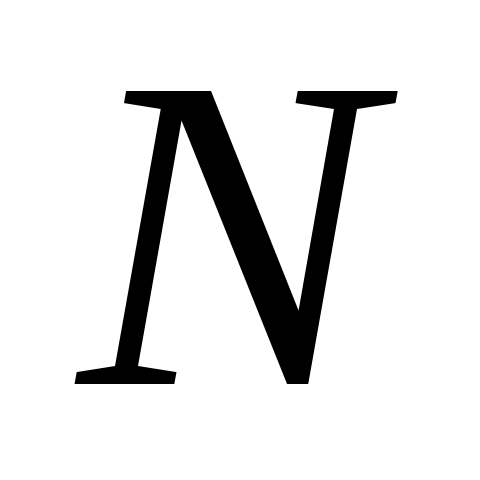 - нечётное составное число, - нечётное составное число, 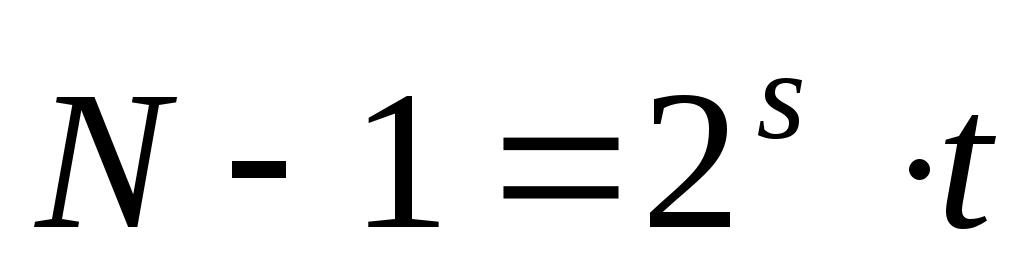 , где , где 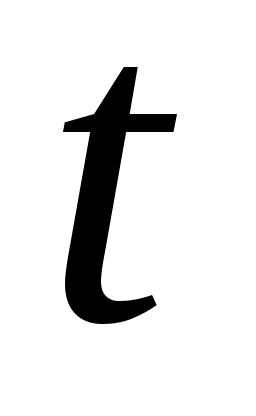 нечётно. Назовем целое число нечётно. Назовем целое число  , , 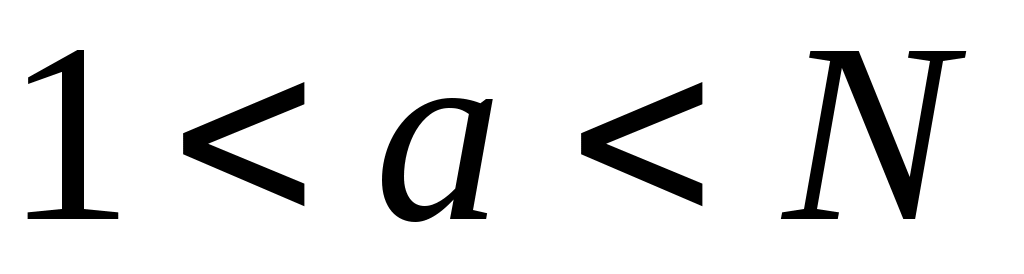 , «хорошим» для , «хорошим» для 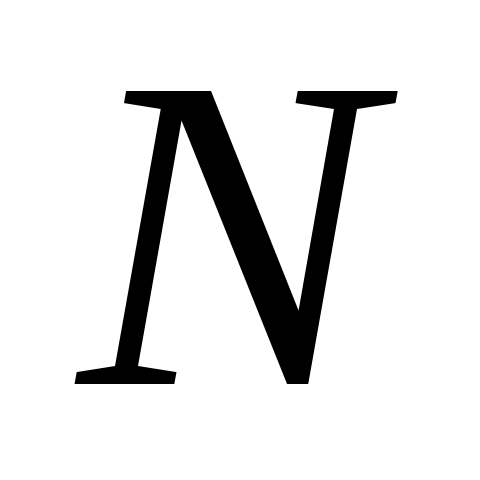 , если нарушается одно из двух условий: , если нарушается одно из двух условий:
1) 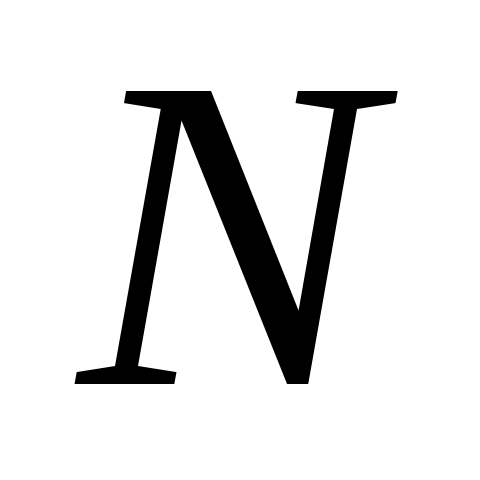 не делится на не делится на  ; ;
2) 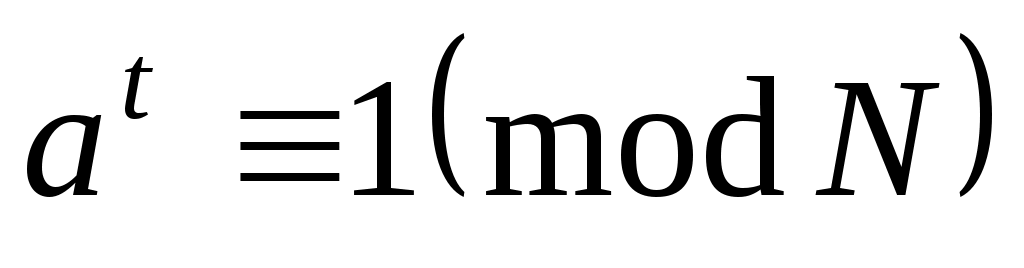 или существует целое или существует целое 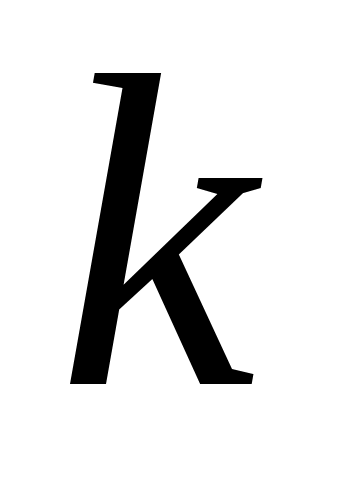 , , 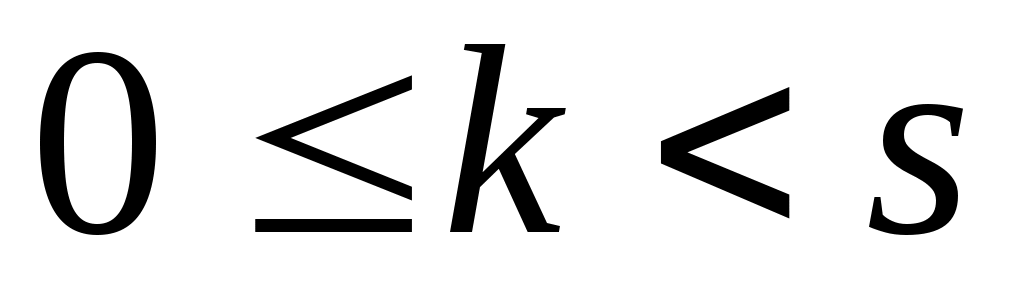 , такое, что , такое, что
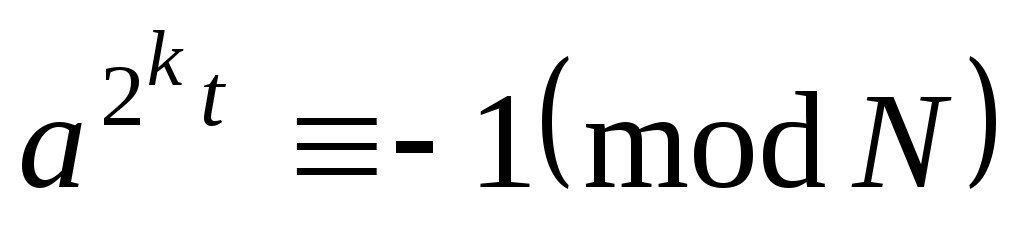 . .
Из сказанного ранее следует, что для простого числа 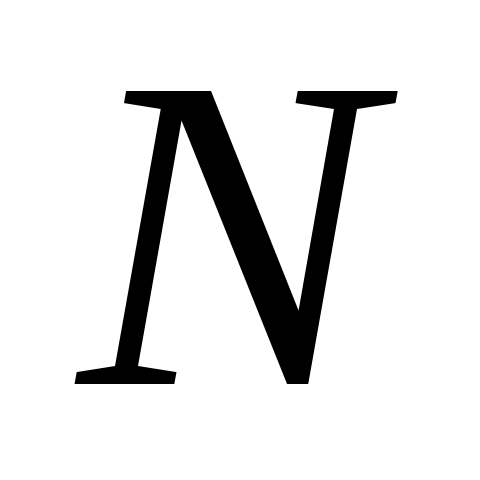 не существует хороших чисел не существует хороших чисел  . Если же . Если же 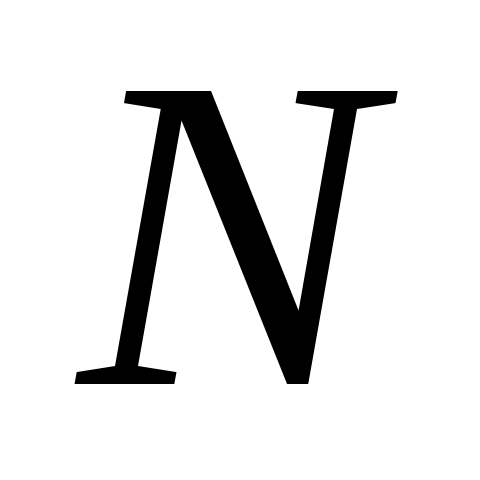 составное число, то, как доказал Рабин, их существует не менее составное число, то, как доказал Рабин, их существует не менее 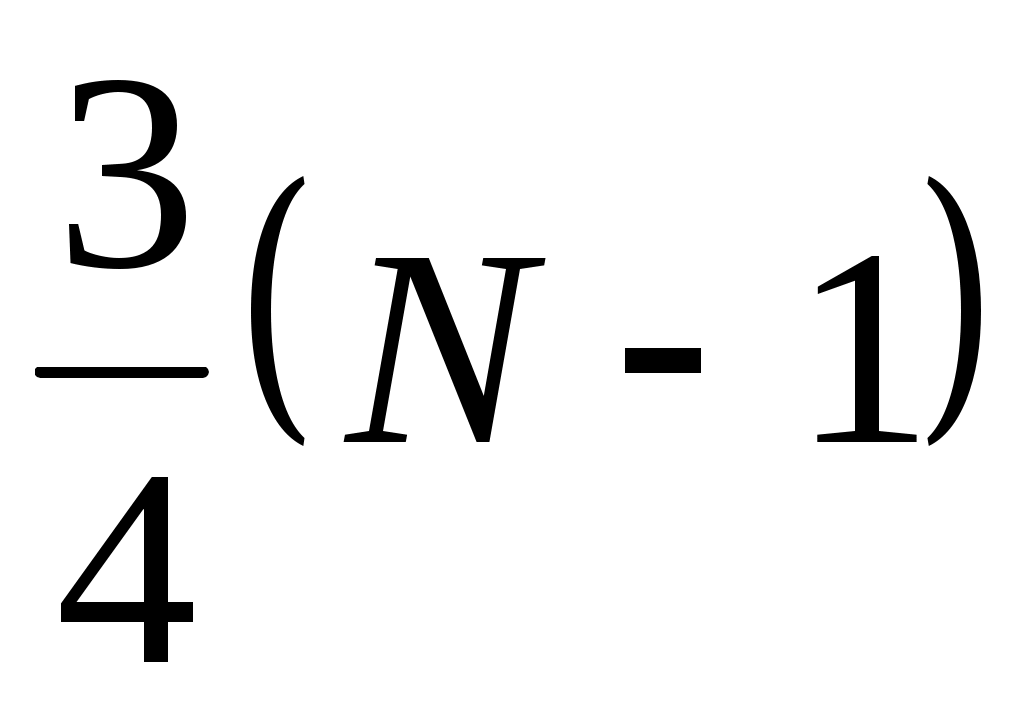 . .
Теперь можно построить вероятностный алгоритм, отличающий составные числа от простых.
3.1. Алгоритм, доказывающий непростоту числа
Выберем случайным образом число  , , 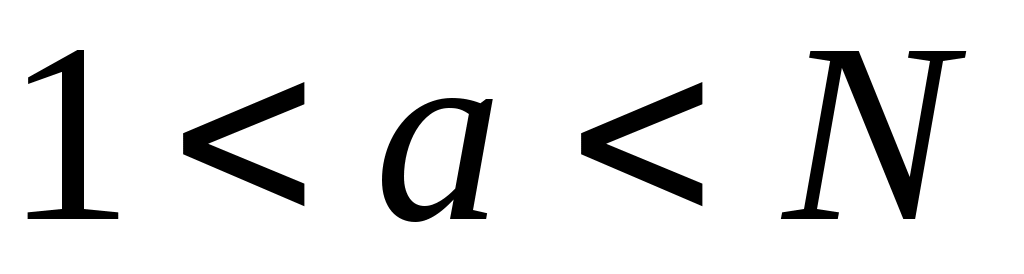 , и проверим для , и проверим для
этого числа указанные выше свойства 1) и 2) п.2.
Если хотя бы одно из них нарушается, то число 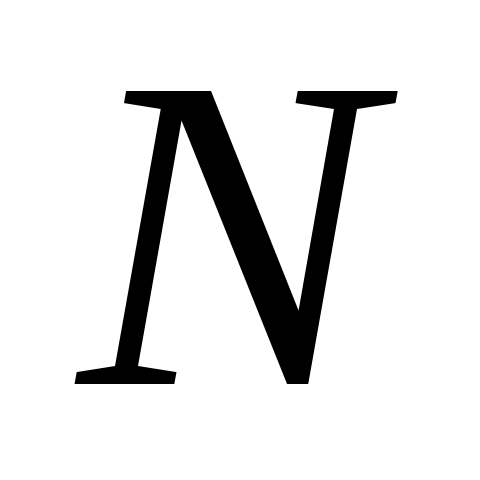 составное. составное.
Если выполнены оба условия 1) и 2) п.2, возвращаемся к шагу 1.
Из сказанного выше следует, что составное число не будет определено как составное после однократного выполнения шагов 1-3 с вероятностью не большей 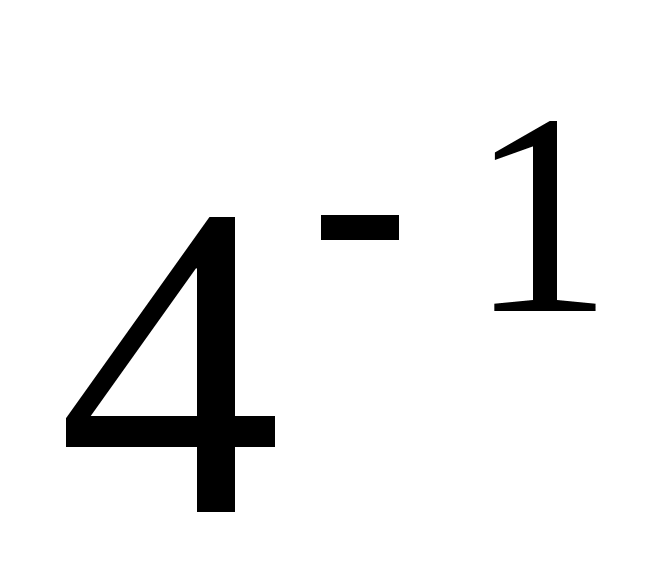 . А вероятность не определить его после . А вероятность не определить его после 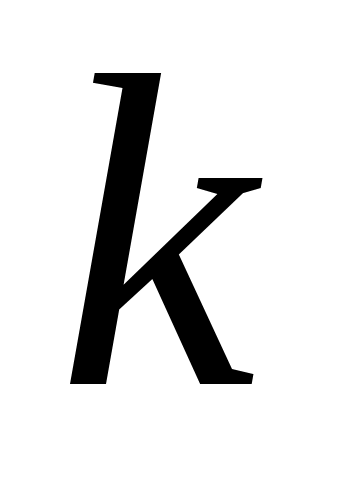 повторений не превосходит повторений не превосходит 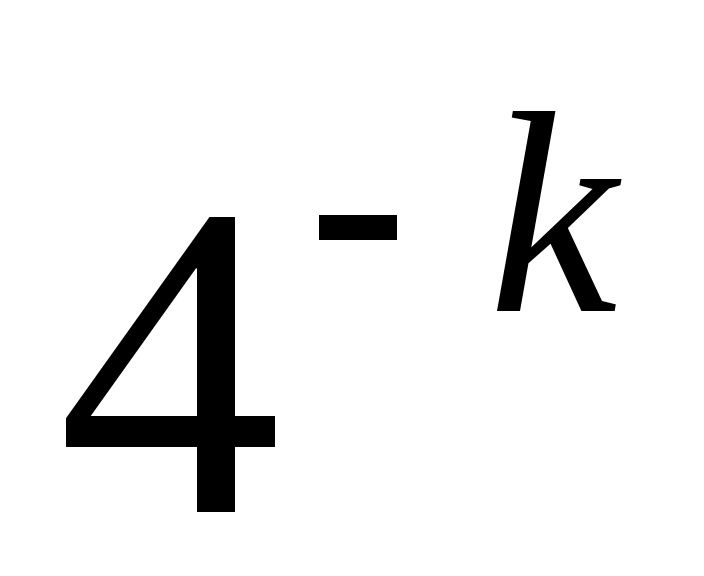 . т. е. убывает очень быстро. . т. е. убывает очень быстро.
Миллер предложил детерминированный алгоритм определения составных чисел, имеющий сложность 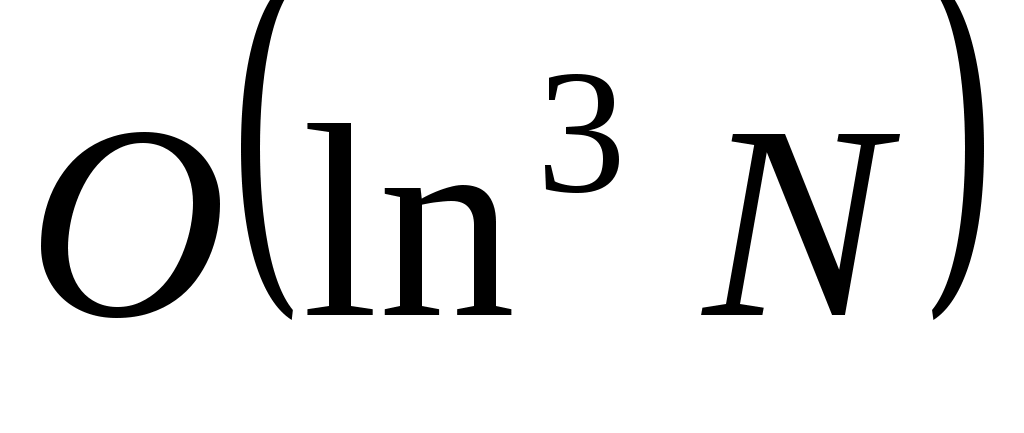 , однако справедливость его результата зависит от недоказанной в настоящее время так называемой расширенной гипотезы Римана. Согласно этому алгоритму достаточно проверить условия 1) и 2) п.2 для всех целых чисел , однако справедливость его результата зависит от недоказанной в настоящее время так называемой расширенной гипотезы Римана. Согласно этому алгоритму достаточно проверить условия 1) и 2) п.2 для всех целых чисел  , ,  . Если при каком-нибудь . Если при каком-нибудь  из указанного промежутка нарушается одно из условий а) или б), число из указанного промежутка нарушается одно из условий а) или б), число 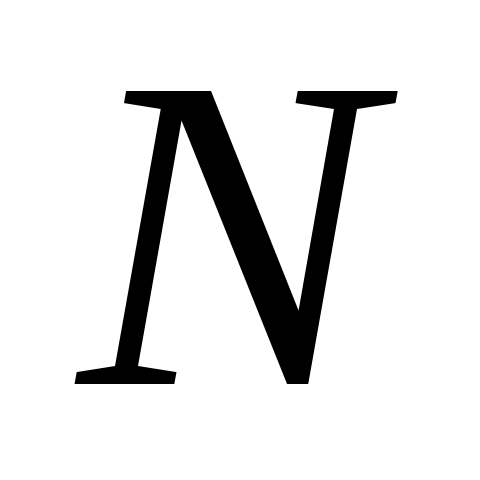 составное. В противном случае оно будет простым или степенью простого числа. Последняя возможность, конечно, легко проверяется. составное. В противном случае оно будет простым или степенью простого числа. Последняя возможность, конечно, легко проверяется.
Напомним некоторые понятия, необходимые для формулировки расширенной гипотезы Римана. Они понадобятся нам и в дальнейшем. Пусть 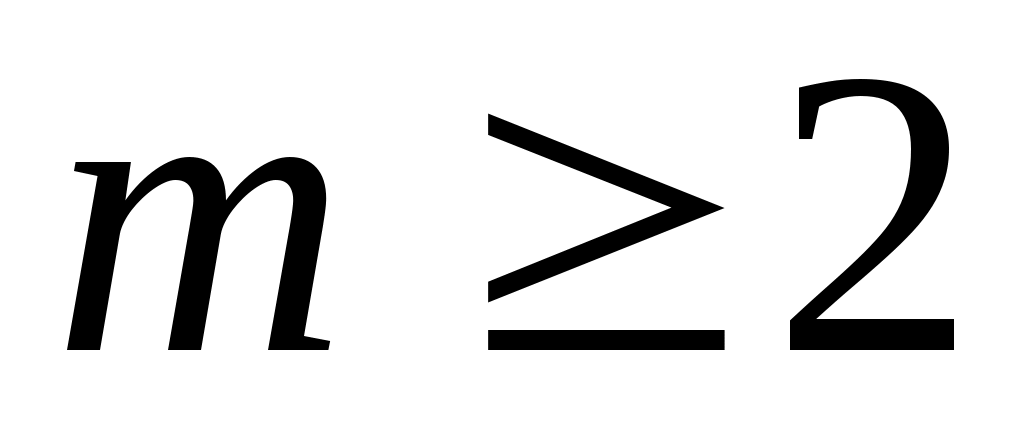 - целое число. Функция - целое число. Функция 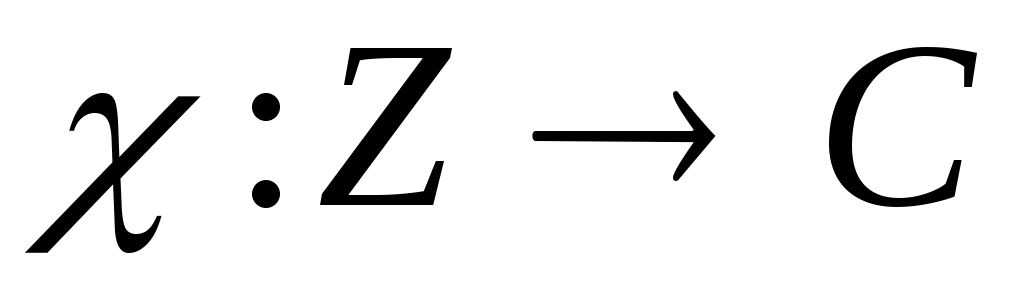 называется характером Дирихле по модулю называется характером Дирихле по модулю 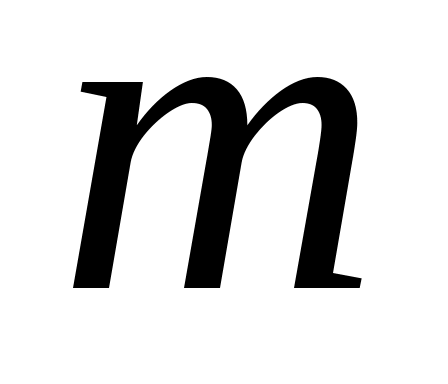 , или просто характером, если эта функция периодична с периодом , или просто характером, если эта функция периодична с периодом 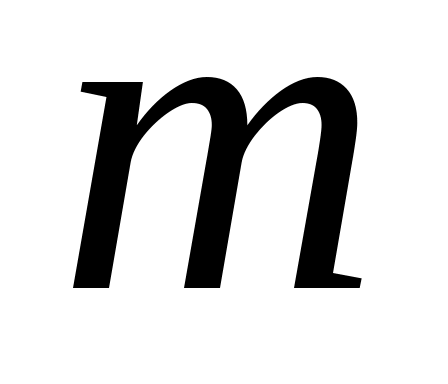 , отлична от нуля только на числах, взаимно простых с , отлична от нуля только на числах, взаимно простых с 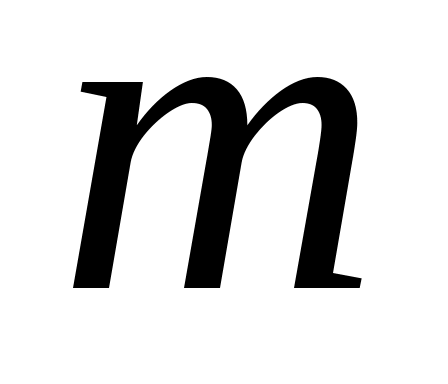 , и мультипликативна, т. е. для любых целых , и мультипликативна, т. е. для любых целых 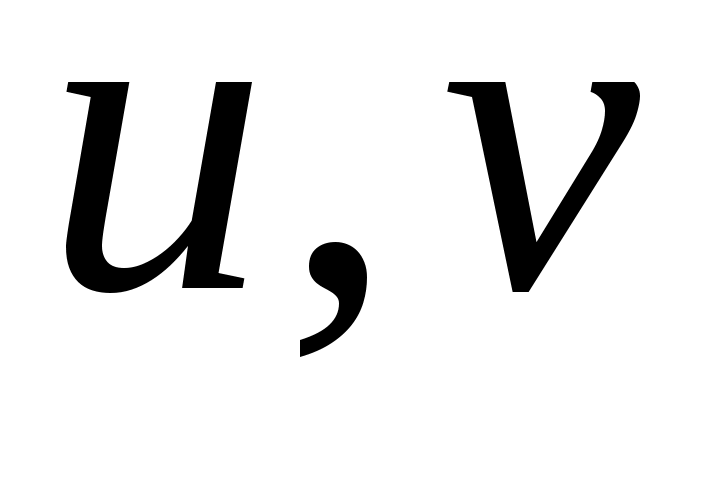 выполняется равенство выполняется равенство 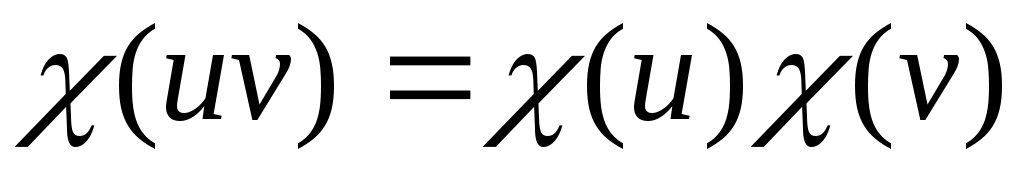 . Для каждого . Для каждого 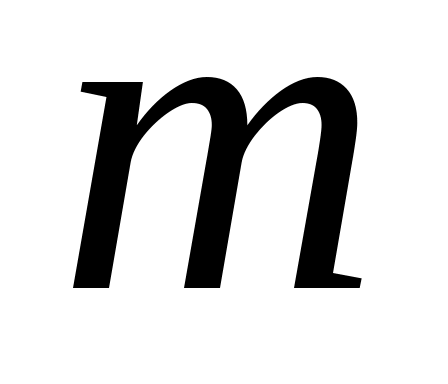 существует ровно существует ровно 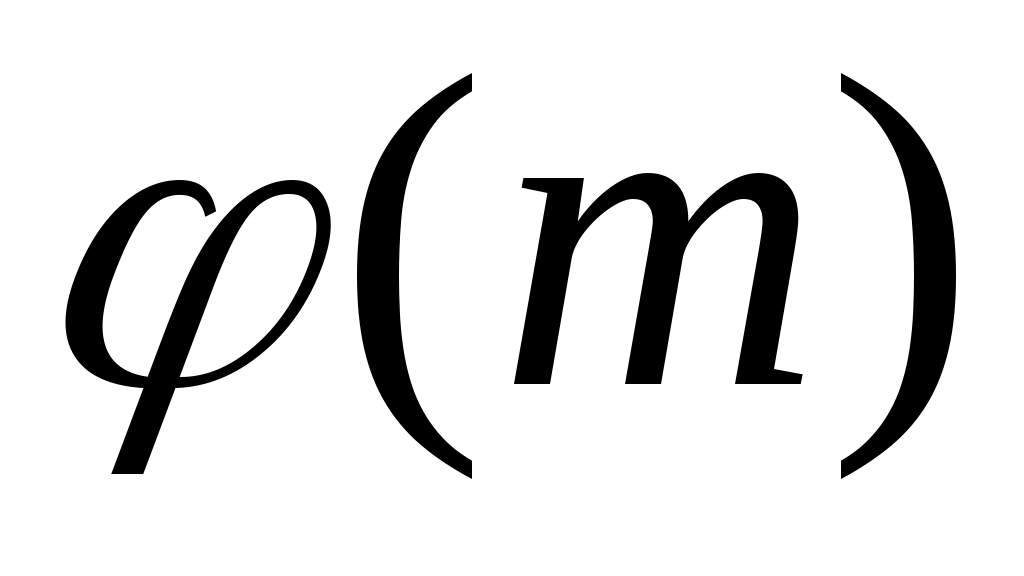 характеров Дирихле. Они образуют группу по умножению. Единичным элементом этой группы является так называемый главный характер характеров Дирихле. Они образуют группу по умножению. Единичным элементом этой группы является так называемый главный характер 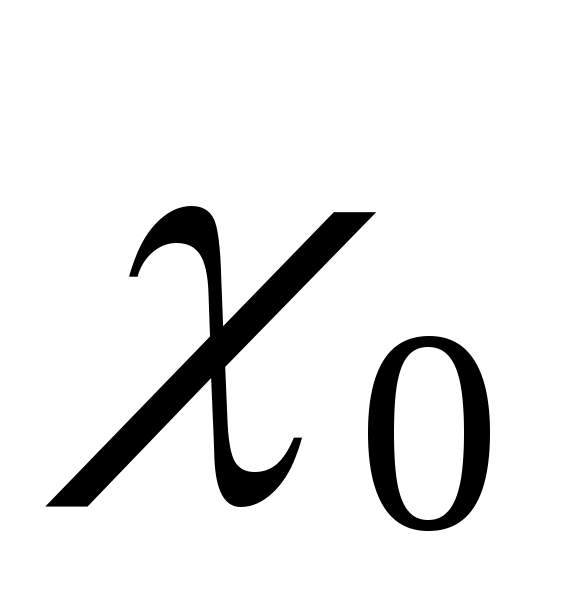 , равный 1 на всех числах, взаимно простых с , равный 1 на всех числах, взаимно простых с 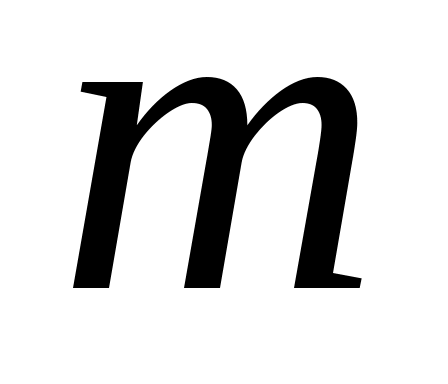 , и 0 на остальных целых числах. Порядком характера называется его порядок как элемента мультипликативной группы характеров. , и 0 на остальных целых числах. Порядком характера называется его порядок как элемента мультипликативной группы характеров.
С каждым характером может быть связана так называемая 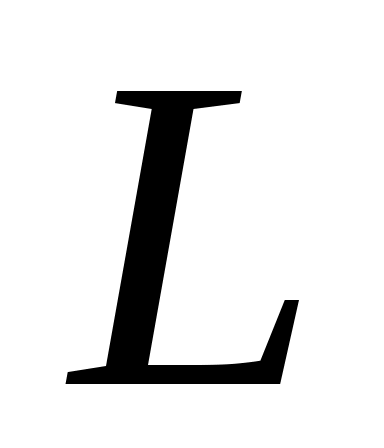 - функция Дирихле - функция комплексного переменного - функция Дирихле - функция комплексного переменного 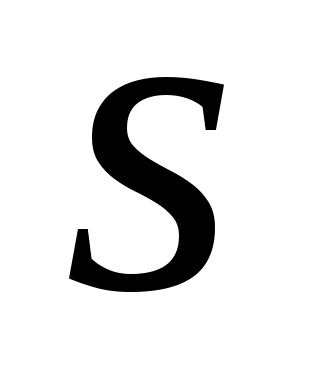 , определённая рядом , определённая рядом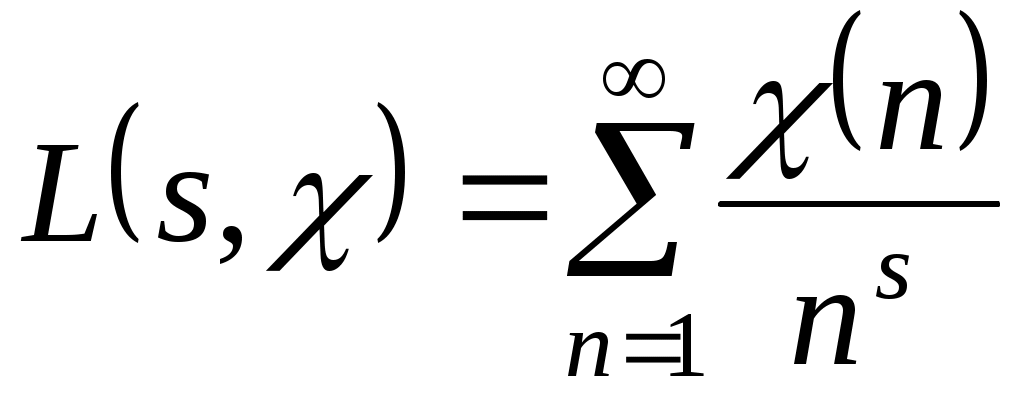 . Сумма этого ряда аналитична в области . Сумма этого ряда аналитична в области 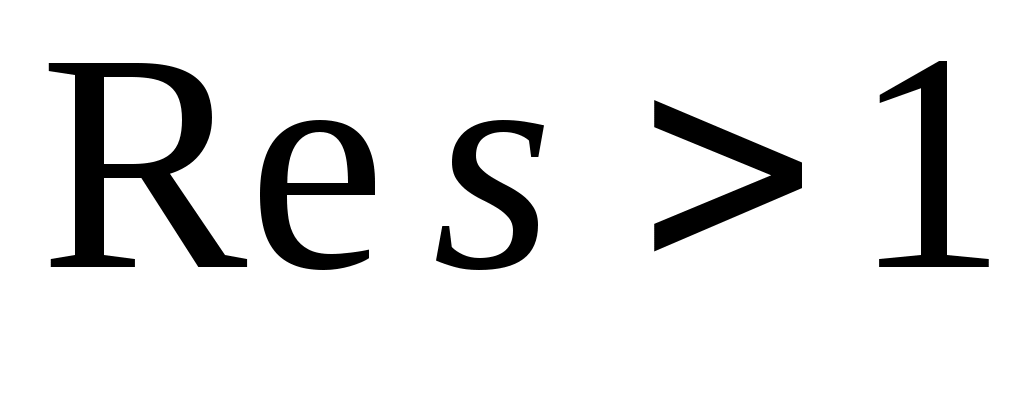 и может быть аналитически продолжена на всю комплексную плоскость. Следующее соотношение и может быть аналитически продолжена на всю комплексную плоскость. Следующее соотношение 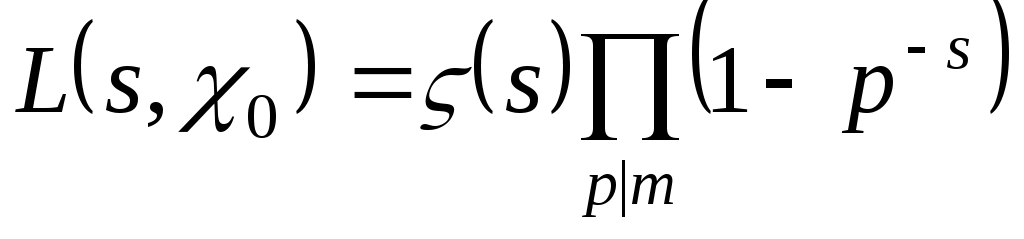 связывает L - функцию, отвечающую главному характеру, с дзета-функцией Римана связывает L - функцию, отвечающую главному характеру, с дзета-функцией Римана 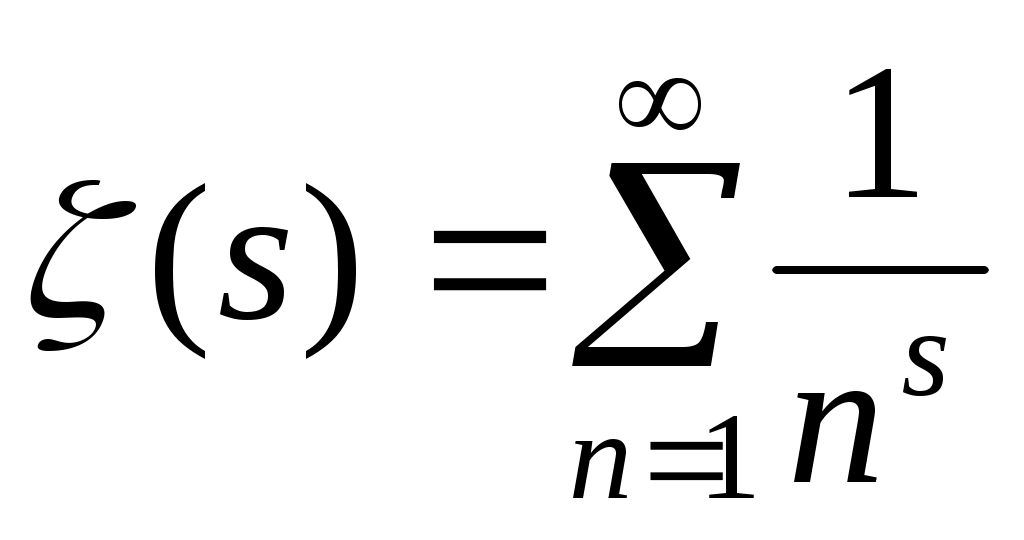 . Расширенная гипотеза Римана утверждает, что комплексные нули всех L -функций Дирихле, расположенные в полосе . Расширенная гипотеза Римана утверждает, что комплексные нули всех L -функций Дирихле, расположенные в полосе 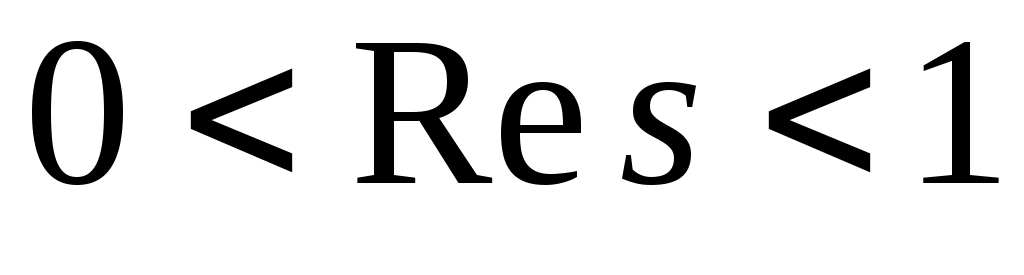 , лежат на прямой , лежат на прямой 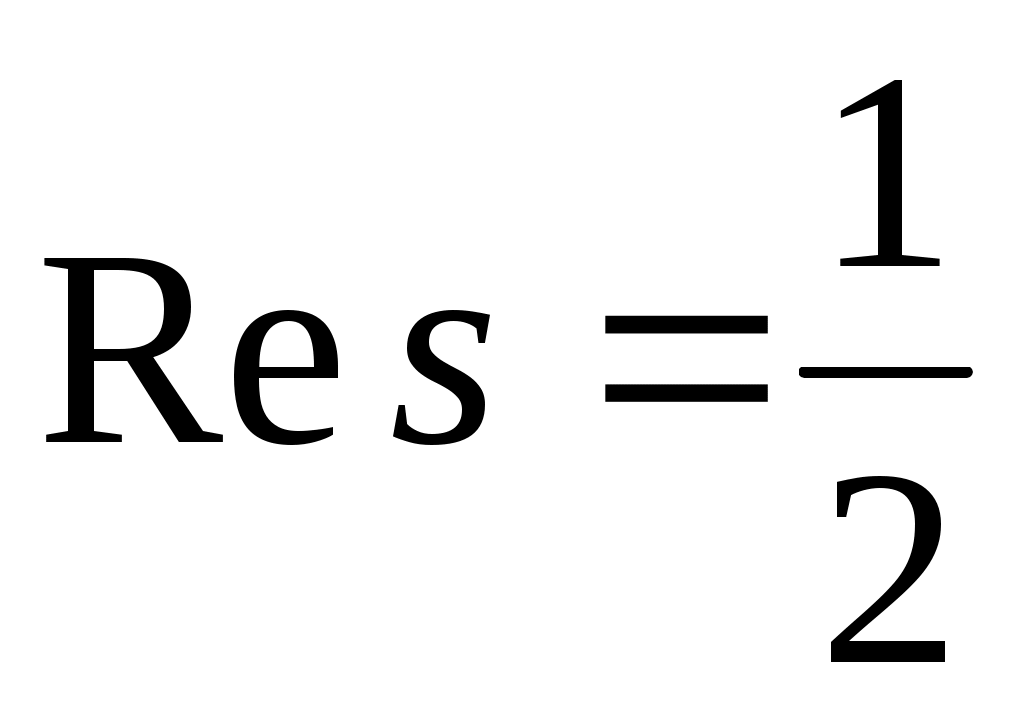 . В настоящее время не доказана даже простейшая форма этой гипотезы - классическая гипотеза Римана, утверждающая такой же факт о нулях дзета-функции. . В настоящее время не доказана даже простейшая форма этой гипотезы - классическая гипотеза Римана, утверждающая такой же факт о нулях дзета-функции.
В 1952 г. Анкени с помощью расширенной гипотезы Римана доказал, что для каждого простого числа 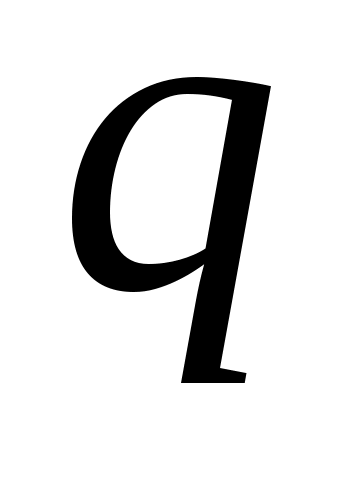 существует квадратичный невычет существует квадратичный невычет  , удовлетворяющий неравенствам , удовлетворяющий неравенствам 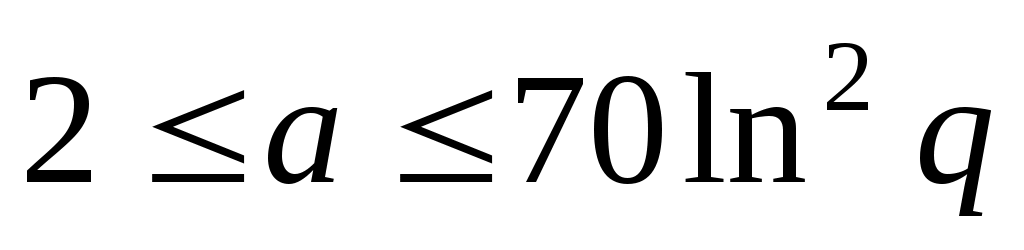 . Константа 70 была сосчитана позднее. Именно это утверждение и лежит в основе алгоритма Миллера. В 1957 г. Берджесс доказал существование такого невычета без использования расширенной гипотезы Римана, но с худшей оценкой . Константа 70 была сосчитана позднее. Именно это утверждение и лежит в основе алгоритма Миллера. В 1957 г. Берджесс доказал существование такого невычета без использования расширенной гипотезы Римана, но с худшей оценкой 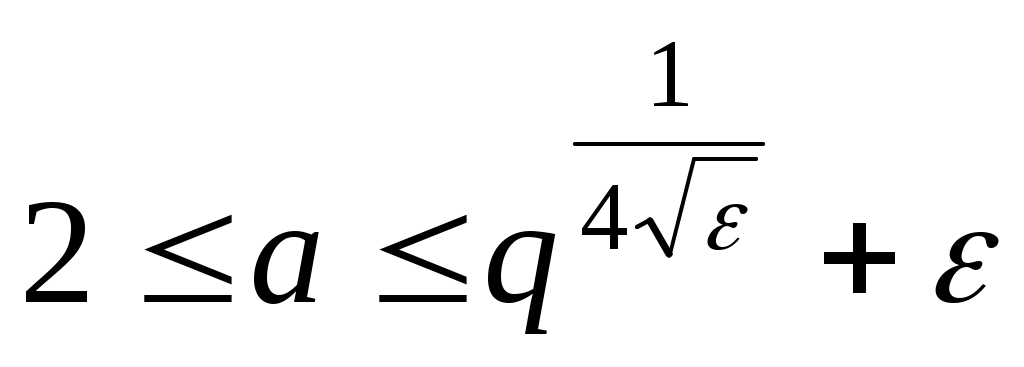 , справедливой при любом положительном , справедливой при любом положительном 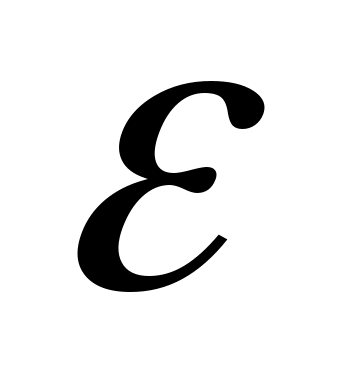 и и 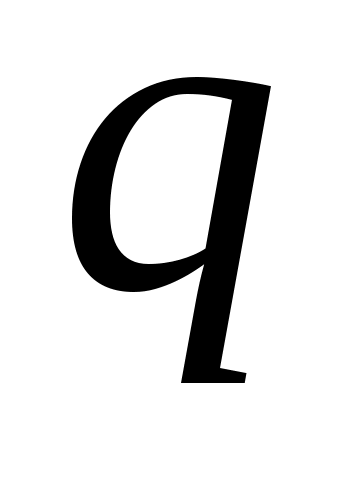 , большем некоторой границы, зависящей от , большем некоторой границы, зависящей от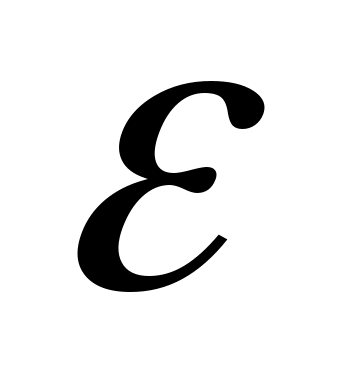 . .
Алгоритм Миллера принципиально отличается от алгоритма 2.1., так как полученное с его помощью утверждение о том, что число 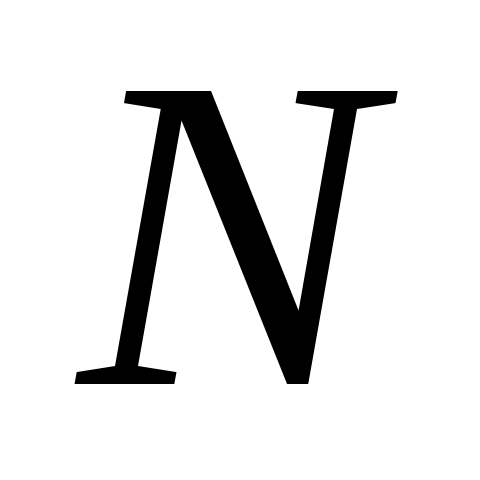 - составное, опирается на недоказанную расширенную гипотезу Римана и потому может быть неверным. В то время как вероятностный алгоритм 2.1. даёт совершенно правильный ответ для составных чисел. Несмотря на отсутствие оценок сложности, на практике он работает вполне удовлетворительно. - составное, опирается на недоказанную расширенную гипотезу Римана и потому может быть неверным. В то время как вероятностный алгоритм 2.1. даёт совершенно правильный ответ для составных чисел. Несмотря на отсутствие оценок сложности, на практике он работает вполне удовлетворительно.
3.2. Нахождение больших простых чисел
Конечно же, большие простые числа можно строить сравнительно быстро. При этом можно обеспечить их случайное распределение в заданном диапазоне величин. В противном случае теряла бы всякий практический смысл система шифрования RSA. Наиболее эффективным средством построения простых чисел является несколько модифицированная малая теорема Ферма.
Теорема 2. Пусть 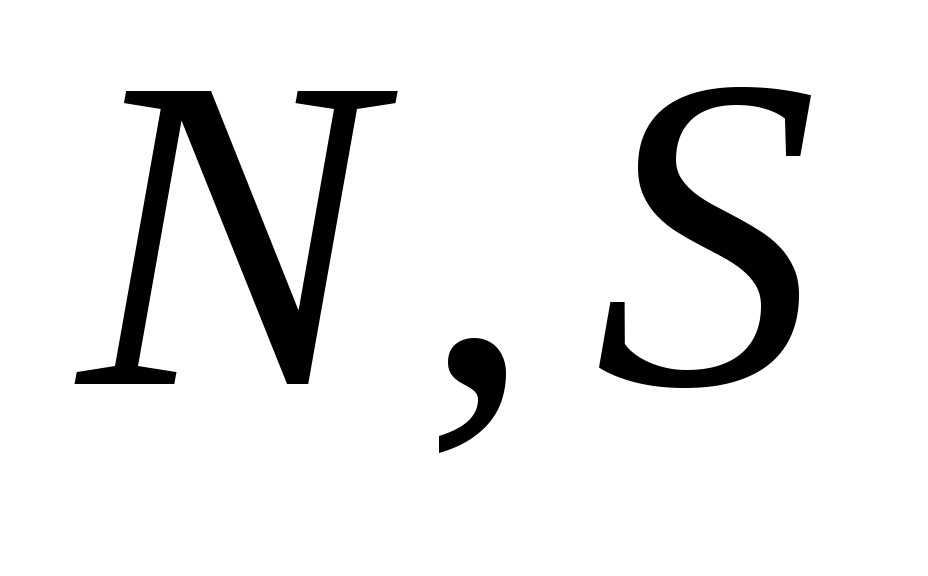 - нечётные натуральные числа, - нечётные натуральные числа, 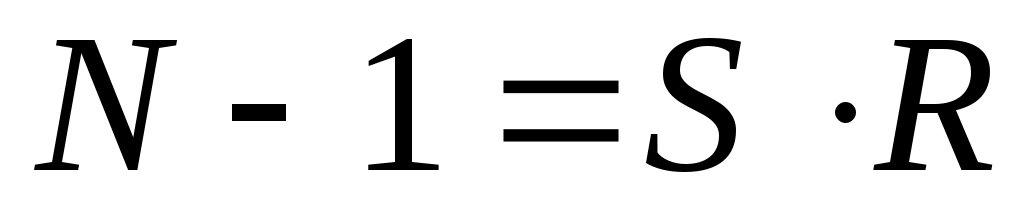 , причем для каждого простого делителя , причем для каждого простого делителя 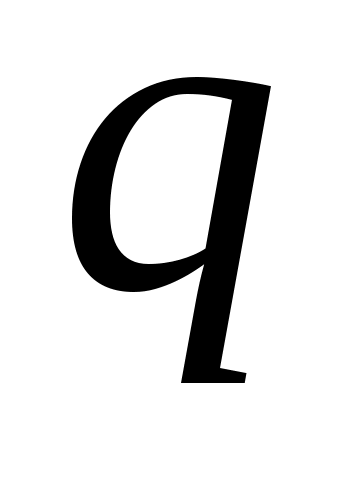 числа числа 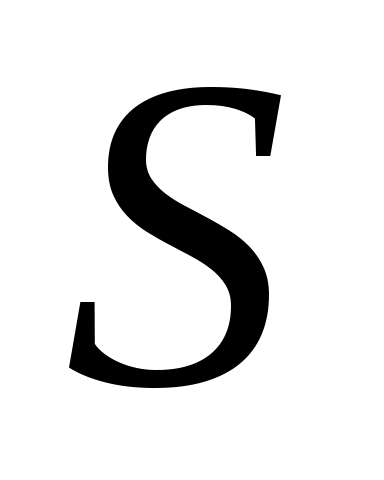 существует целое число существует целое число  такое, что такое, что
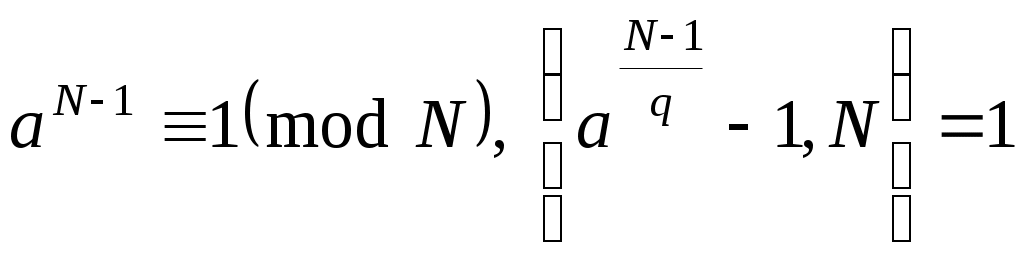 . (10) . (10)
Тогда каждый простой делитель 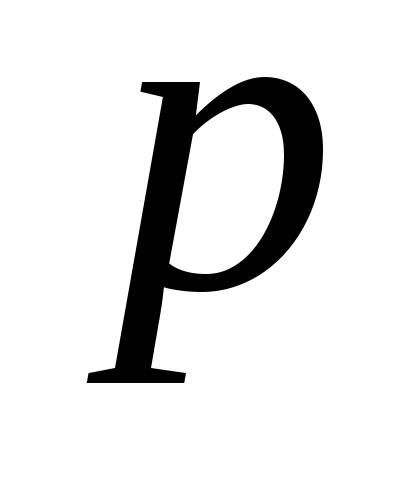 числа числа 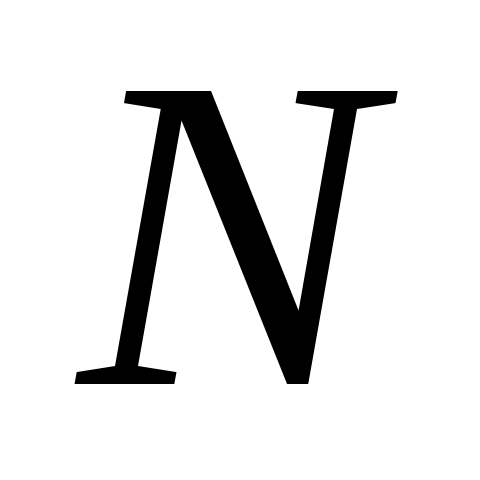 удовлетворяет сравнению удовлетворяет сравнению
|
 Скачать 1.17 Mb.
Скачать 1.17 Mb.