ДИПЛОМНАЯ РАБОТА на тему Применение алгоритма RSA при шифровании. Применение алгоритма rsa при шифровании потоков данных
 Скачать 1.17 Mb.
|
 , что позволяет доказывать простоту чисел  , записываемых сотней десятичных знаков. При этом вычисления будут проводиться в полях, порождённых корнями из 1 степеней 16, 9, 5 и 7.Персональный компьютер с процессором Pentium-150. пользуясь реализацией этого алгоритма на языке UBASIC, доказал простоту записываемого 65 десятичными знаками, большего из простых чисел в примере Ривеста, Шамира и Адлемана за 8 секунд. Сравнение этих 8 секунд и 17 лет, потребовавшихся для разложения на множители предложенного в примере числа, конечно, впечатляет. Отметим, что опенка сложности этого алгоритма представляет собой трудную задачу аналитической теории чисел. Как уже указывалось, количество операций оценивается величиной  . Однако соответствующие числа  и  , возникающие в процессе доказательства, не могут быть явно указаны в зависимости от . Доказано лишь существование чисел и , для которых достигается оценка. Впрочем, есть вероятностный вариант алгоритма, доказывающий простоту простого числа с вероятностью большей  за  арифметических операций. А в предположении расширенной гипотезы Римана эта опенка сложности может быть получена при эффективно указанных и .4. ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ АЛГОРИТМА Представленный выше алгоритм шифрования был реализован с помощью интегрированного пакета фирмы Borland Delphi 5.0. Выбор данного языка программирования обоснован тем что, он предоставляет такие возможности, как объектно-ориентированный подход к программированию, основанный на формах, интеграция с программированием для Windows и компонентная технология. Среду визуального программирования Delphi 5 позволяет с помощью компонентного подхода к созданию приложений, быстро и качественно "собрать" интерфейс программы и большую часть времени использовать именно на реализацию составленного алгоритма. Программа построена по технологии клиент/сервер, т.е. клиент передает по сети данные из стандартного потока ввода (с клавиатуры), предварительно зашифровав, сервер, получая поток данных, автоматически его расшифровывает. Программный продукт состоит из двух приложений. Первое приложение представляет собой программу генерации ключей. Она выводит все простые числа заданного диапазона, из которых потом выбираются числа  и  . Там же находятся открытый и закрытый ключи, которые сохраняются на диске. Второе приложение, основная программа, производит соединение между двумя компьютерами и, отправляя сообщение, шифрует его. Это приложение клиент. Приложение сервер получает сообщение и расшифровывает его. Так же во второй программе содержится небольшая база данных абонентов, хранящая в себе имена абонентов, IP адреса и их открытые ключи.4.1. Реализованные алгоритмы В программном продукте были реализованы основные алгоритмы схемы RSA. Функция ModDegree производит вычисление  . Функция Prost находит все простые числа заданного диапазона. Функция Evklid реализует алгоритм Евклида и находит закрытый ключ  . Функция HOD производит вычисление наибольшего общего делителя и находит открытый ключ  . Вышеперечисленные функции представлены в приложении 1. 4.2. Анализ результатов Результатом работы созданной программы являются зашифрованные и расшифрованные сообщения. Для тестирования программы использовался пример приведенный в [11]  ,  ,  и  . Также  и  . 5. ВЫВОДЫ Перейдем к обсуждению выводов после детального просмотра специфики метода, реализованного программного продукта на основе построенного алгоритма, а также представленного анализа результатов по обработанному материалу. 5.1 Алгоритм Использованный алгоритм RSA имеет ряд преимуществ: 1) алгоритм RSA является ассиметричным, т.е. он основывается на распространении открытых ключей в сети. Это позволяет нескольким пользователям обмениваться информацией, посылаемой по незащищенным каналам связи; 2) пользователь сам может менять как числа , , так и открытый и закрытый ключ по своему усмотрению, только потом он должен распространить открытый ключ в сети. Это позволяет добиваться пользователю нужной ему криптостойкости.При всех этих преимуществах данный алгоритм имеет существенный недостаток – невысокая скорость работы. Алгоритм RSA работает более чем в тысячу раз медленнее симметричного алгоритма DES. Из всего вышесказанного можно заключить, что данный алгоритм шифрования, хотя довольно медленный, но он ассиметричный и позволяет добиваться нужной криптостойкости, что делает его незаменимым при работе в незащищенных каналах связи. 5.2 Алгоритм и программа Исходя из проработанных данных, по построенному алгоритму и созданному программному продукту сделаны следующие выводы: 1) построенный алгоритм, а соответственно и созданный на его базе программный продукт, полностью реализует базовые механизмы схемы RSA и, таким образом удовлетворяют основным поставленным задачам; 2) данный программный продукт построен по технологии клиент/сервер и предназначен сохранять конфиденциальность передачи информации в сети. Таким образом, по выводам о построенном алгоритме и созданном программном продукте можно заключить, что он подходит для решения проблем шифрования информации, связанных с передачей данных по сети. ЗАКЛЮЧЕНИЕ В рамках данного дипломного проектирования перед студентом Малышевым А.А. была поставлена задача: на основе алгоритма RSA для шифрования блоков данных, построить алгоритм и реализовать программный продукт для шифрования потоков данных. В результате выполнения дипломного проектирования был составлен принципиальный алгоритм для решения поставленной задачи. Далее он был детализован и реализован на ЭВМ. В конце, был проведён анализ полученных результатов, и сделаны необходимые выводы. За основу построения алгоритма был принят алгоритм RSA для шифрования блоков данных, изучена соответствующая литература по алгоритму, и был построен алгоритм и реализован программный продукт в среде визуального программирования Delphi 5 под ОС типа Windows для IBM PC-совместимых компьютеров. Созданный программный продукт позволяет решить поставленную задачу и, дополнительно, содержит в себе небольшую базу данных абонентов. Т.е. в результате выполнения программы исходное сообщение шифруется и передается по сети, где оно расшифровывается. Также можно указать о том, что программа имеет интуитивно понятный интерфейс, что дополнительно помогает пользователю с наибольшей результативностью использовать всю ресурсную базу. В заключении, после анализа полученных результатов были сделаны выводы, согласно которым алгоритм работает и применим для поставленной задачи. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 1. Ященко В. В. Основные понятия криптографии // Математическое просвещение. Сер. 3. №2. 1998. С. 53-70. 2. Виноградов И. М. Основы теории чисел. М.: Наука. 1972. 3. Карацуба А. А. Основы аналитической теории чисел. М.: Наука. 1983 г. 4. Кнут Д. Искусство программирования на ЭВМ. Т.2: Получисленные алгоритмы. М.: Мир. 1977. 5. Ахо А.. Хопкрофт Дж.. Ульман Дж. Построение и анализ вычислительных алгоритмов. М.: Мир. 1979. 6. Варновский Н. П. Криптография и теория сложности // Математическое просвещение. Сер. 3. №2. 1998. С. 71-86. 7. Василенко О. Н. Современные способы проверки простоты чисел // Кибернетический сборник, вып. 25. 1988. С. 162-188. 8. Прахар К. Распределение простых чисел. М.: Мир. 1967. 9.Боревич З.И. Шафаревич И.Р. Теория чисел. М.: Наука. 1964. 10. Кострикин А.И. Введение в алгебру. М.: Наука. 1977. 11. Брассар Дж. Современная криптология. Мир ПК. №3. 1997. ПРИЛОЖЕНИЕ 1 Листинг программы Модуль Key.pas Function Prost(n:integer):Boolean; var k:Boolean; i:integer; begin k:=true; if n<>2 then for i:=2 to trunc(sqrt(n))+1 do if (n/i)=trunc(n/i) then begin k:=False; Break; end; Prost:=k; end; {________________________________________________________} Function Evklid(Num1,Num2:integer):integer; var r,q1,p1:array of integer; i,n,k:integer; begin if Num1>=Num2 then begin SetLength(r,10); r[0]:=Num1; r[1]:=Num2; end else begin SetLength(r,10); r[0]:=Num2; r[1]:=Num1; end; i:=1; while r[i]<>0 do begin inc(i); r[i]:=r[i-2] mod r[i-1]; end; n:=i-2; SetLength(q1,n+1); for i:=0 to n do q1[i]:=r[i] div r[i+1]; SetLength(p1,n+2); p1[0]:=1; p1[1]:=q1[0]; k:=length(q1); if k>1 then for i:=2 to k do p1[i]:=q1[i-1]*p1[i-1]+p1[i-2]; Result:=trunc(power(-1,k-1))*p1[k-1] mod Num2; end; {________________________________________________________} Function HOD(Num1,Num2:integer):integer; var r:array of integer; i:integer; begin if Num1>=Num2 then begin SetLength(r,Num2); r[0]:=Num1; r[1]:=Num2; end else begin SetLength(r,Num1); r[0]:=Num2; r[1]:=Num1; end; i:=1; While r[i]<>0 do begin inc(i); r[i]:=r[i-2] mod r[i-1]; end; Result:=r[i-1]; end; {________________________________________________________} Function ModDegree(Num,Degree,n:integer):integer; var x:array of integer; i:integer; begin SetLength(x,n); x[1]:=Num mod n; for i:=2 to Degree do x[i]:=x[i-1]*Num mod n; Result:=x[Degree]; end; ПРИЛОЖЕНИЕ 2 Главная форма программы 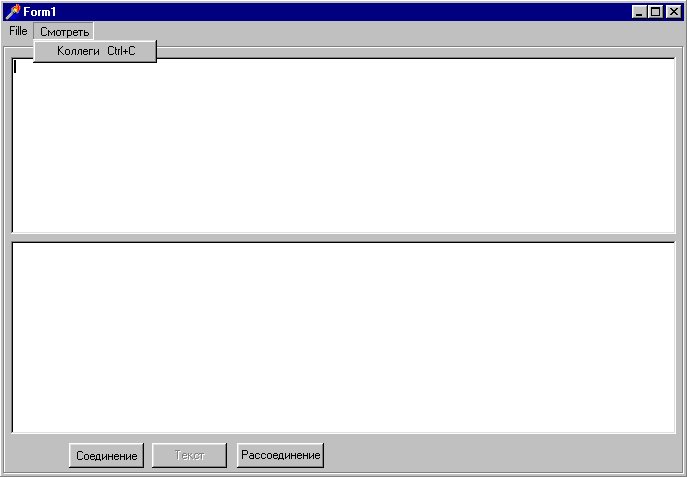 ПРИЛОЖЕНИЕ 3 Форма базы данных абонентов 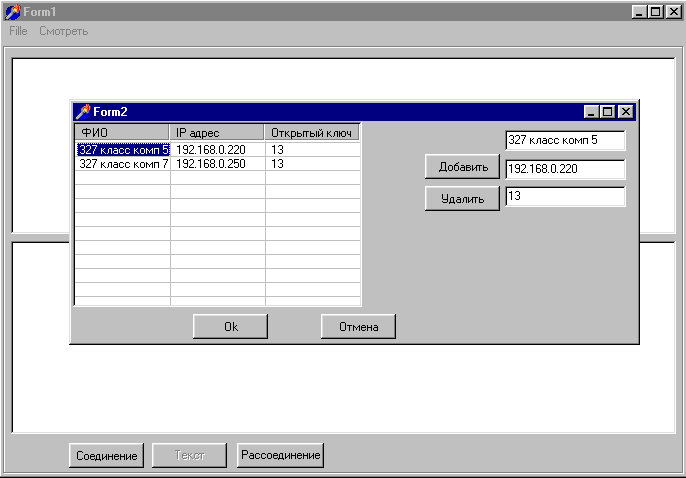 ПРИЛОЖЕНИЕ 4 Форма нахождения простых чисел и генерации ключей 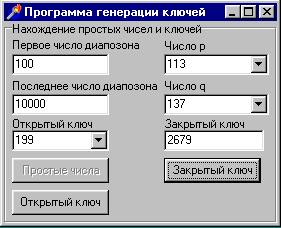 |