Работа готовая. Применение метода байеса для косвенной диагностики состояния объектов
 Скачать 79.61 Kb. Скачать 79.61 Kb.
|
|
СОДЕРЖАНИЕ ВВЕДЕНИЕ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 ПРИМЕНЕНИЕ МЕТОДА БАЙЕСА ДЛЯ КОСВЕННОЙ ДИАГНОСТИКИ СОСТОЯНИЯ ОБЪЕКТОВ . . . . . . . . . . . . . . . . . . . . . . . 5 САМОСТОЯТЕЛЬНЫЙ РАСЧЕТ ДИАГНОЗА ОПОРЫ ПО ВАРИАНТАМ ЗАДАНИЙ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9 СПИСОК ЛИТЕРАТУРЫ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 ВВЕДЕНИЕ Термин «диагностика» происходит от греческого слова «диагнозис», что означает распознавание, определение. Технической диагностикой называется наука о распознавании технического состояния объекта. Целью технической диагностики является повышение надёжности и ресурса, технических изделий. Наиболее важным показателем надёжности изделия является отсутствие отказов во время его функционирования (безотказность), так как отказ изделия может привести к тяжёлым последствиям. Техническая диагностика, благодаря раннему обнаружению дефектов и неисправностей, позволяет устранить подобные отказы в процессе технического обслуживания и ремонта, что повышает надёжность и эффективность эксплуатации изделий. Техническая диагностика решает обширный круг задач, многие из которых являются смежными с задачами других научных дисциплин. Основной задачек технической диагностики является распознавание технического состояния объекта в условиях ограниченной информации. Анализ состояния проводится в условиях эксплуатации, при которых получение информации крайне затруднено, поэтому часто не представляется возможным по имеющейся информации сделать однозначное заключение, и приходится использовать статистические методы. Теоретическим фундаментом для решения основной задачи технической диагностики следует считать общую теорию распознавания образов. Техническая диагностика изучает алгоритмы распознавания применительно к задачам диагностики, которые обычно могут рассматриваться как задачи классификации. Алгоритмы распознавания в технической диагностике частично основываются на диагностических моделях, устанавливающих связь между техническими состояниями изделия и их отображениями в пространстве диагностических признаков. Важной частью проблемы распознавания являются правила принятия решений (решающие правила). Решение диагностических задач (отнесение изделия к исправным или неисправным) всегда связано с риском ложной тревоги или пропуска цели. Для принятия обоснованного решения привлекаются методы теории статистических решений. Решение задач технической диагностики связано с прогнозированием надёжности на ближайший период эксплуатации (до следующего технического осмотра). Здесь решения основываются на моделях отказов, изучаемых в теории надёжности. Другим важным направлением технической диагностики является теория контролеспособности. Контролеспособностью называется свойство изделия обеспечивать достоверную оценку его технического состояния. Контролеспособность создаётся конструкцией изделия и принятой системой диагностики. Основной задачей теории контролеспособности является изучение средств и методов получения диагностической информации. в сложных технических системах используется автоматизированный контроль состояния, которым предусматривается обработка диагностической информации и формирование управляющих сигналов. Методы проектирования автоматизированных систем контроля составляют одно из направлений теории контролеспособности. Задачи теории контролеспособности связаны с разработкой алгоритмов поиска неисправностей, разработкой диагностических тестов, минимизацией процесса установления диагноза. Таким образом, структура технической диагностики характеризуется двумя взаимопроникающими и взаимосвязанными направлениями: теорией распознавания и теорией контролеспособности. Теория распознавания содержит разделы, связанные с построением алгоритмов распознавания, решающих правил и диагностических моделей. Теория контролеспособности включает разработку средств и методов получения диагностической информации, автоматизированный контроль и поиск неисправностей. Техническую диагностику можно рассматривать как раздел общей теории надёжности. Качество изделий представляет совокупность свойств, определяющих их пригодность для эксплуатации. Надёжность является важнейшим технико-экономическим показателем качества любого, технического устройства, в частности электрической машины, определяющим её способность безотказно работать с неизменными техническими характеристиками в течение заданного промежутка времени при определённых условиях эксплуатации. Проблема обеспечения надёжности связана со всеми этапами создания изделия и всем периодом его практического использования. Надёжность изделия закладывается в процессе его конструирования и расчёта и обеспечивается в процессе его изготовления путём правильного выбора технологии производства, контроля качества исходных материалов, полуфабрикатов и готовой продукции, контроля режимов и условий изготовления. Надёжность сохраняется применением правильных способов хранения изделий и поддерживается правильной эксплуатацией его, планомерным уходом, профилактическим контролем и ремонтом 1. ПРИМЕНЕНИЕ МЕТОДА БАЙЕСА ДЛЯ КОСВЕННОЙ ДИАГНОСТИКИ СОСТОЯНИЯ ОБЪЕКТОВ Метод Байеса является одним из наиболее простых и мощных методов. Этот метод основан на вычислении условной вероятности появления такого события как диагноз Di при появлении конкретной реализации комплекса признаков К*. Рассмотрим первоначально основные положения этого метода на простейшем случае, когда имеется диагноз Di и один бинарный признак Кj, встречающийся при появлении этого диагноза. Определим некоторые понятия: 1. P(Di) - априорная (до опытная) вероятность появления диагноза Di. Эту вероятность определяют по статистическим данным на начальном этапе применения метода исходя из следующих соображений. Если при обследовании N объектов диагноза установлено, что из них Ni имеют диагноз Di, то вероятность появления этого диагноза определяется соотношением: 2. Р(Кj/Di) - априорная условная вероятность появления признака Кj у объектов, имеющих техническое состояние (диагноз) Di. Эта вероятность так же определяется на начальном этапе по имеющимся статистическим данным. Если из N обследованных объектов Ni находилось в диагнозе Di, а из них Nij объектов имели признак Kj, то условная вероятность появления признака Кj у объектов с диагнозом Di вычисляется следующим образом: 3. P(Kj) - априорная вероятность появления признака Kj у всех объектов независимо от их состояния. То есть, если из N объектов независимо от их технического состояния у Nj был обнаружен признак Kj, то эта вероятность определяется следующим соотношением: 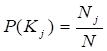 Напомним некоторые положения теории вероятностей. Пусть мы имеем два события А и В. Известны вероятности появления этих событий Р(А) и Р(В), а также условная вероятность появления события А при уже состоявшемся событии В Р(А/В) и условная вероятность появления события В при уже состоявшемся событии А Р(В/А). Тогда вероятность одновременного появления событий А и В Р(А,В) определяется следующей формулой: показатель надежность восстанавливаемый байес Р (А, В) = Р(А) Р(В/А) = Р(В) Р(А/В). Воспользовавшись этой формулой и данными выше понятиями можно записать вероятность одновременного появления диагноза Di и признака Kj следующим образом: P (Di,Kj) =P(Di) P(Kj/Di)=P(Kj) P(Di/Kj). В этом выражении величина P(Di/Кj) - это условная вероятность существования диагноза Di при обнаружении признака Kj, то есть это та величина, которая ищется при вероятностном подходе к решению задачи распознавания диагнозов. После соответствующих преобразований из последнего выражения получим формулу Байеса: P (Di/Kj)={P(Di) P(Kj/Di)}/ P(Kj). (1) Формула (1) получена для случая, когда при постановке диагноза используется один простой признак. Для принятия решения о диагнозе при использовании набора (комплекса) признаков применяется обобщенная формула Байеса, которую можно получить из следующих соображений. Если диагностирование проводится по комплексу признаков, то в результате обследования мы получаем конкретную реализацию каждого j-того признака Kj* и, следовательно, конкретную реализацию комплекса признаков К* в целом. В этом случае формула Байеса предстанет в виде: (2) 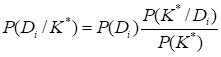 где P(Di/К*) - условная вероятность нахождения объекта диагностики в диагнозе Di при условии, что в ходе обследования была получена реализация К* комплекса признаков К; Р(К*) -вероятность появления конкретной реализации К* комплекса признаков К у всех диагностируемых объектов, независимо от их технического состояния; Р(К*/Di) - условная вероятность появления конкретной реализации К* комплекса диагностических признаков К для объектов, находящихся в диагнозе Di. Преобразуем последние выражения с учетом следующих соображений. Примем, что система может находится только в одном из n технических состояний, тогда: . Будем считать, что отдельные диагностические признаки, входящие в состав комплекса признаков, независимые. Такое допущение вполне справедливо для реальных условий при большом числе влияющих факторов. Тогда условную вероятность Р(К*/Di) в соответствии с известными положениями теории вероятностей можно представить, как произведение: 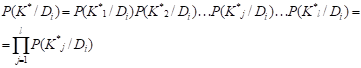 где P(K*j/Di) - условная вероятность появления конкретной реализации К*j j-того признака при нахождении объекта диагностики в диагнозе Di; j= 1... l. Вероятность же появления конкретной реализации комплекса признаков при нахождении объекта во всех диагнозах Р(К*) можно представить следующим образом: 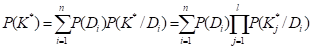 . С учетом последних соотношений уравнение (2) перепишем в окончательном виде: 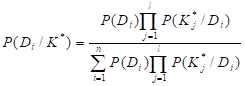 (3) Полученное уравнение называется обобщённой формулой Байеса. В большинстве практических задач, особенно при большом числе признаков, можно принимать условие независимости признаков даже при наличии существенных корреляционных связей между ними и тогда: (4) Для определения вероятности диагноза по методу Байеса составляется исходная диагностическая матрица (табл. 1.1), которая формируется на основе предварительного статистического материала. В этой таблице содержатся вероятности разрядов признаков P(Kjs/Di) при различных диагнозах. Если признаки двухразрядные (простые признаки "да-нет"). то в табл. 1.1 достаточно указать вероятность появления признака P(Kj/Di). Вероятность отсутствия признака: (5) Сумма вероятностей всех реализаций признака Кjравна единице: . При методе Байеса используется следующее правило: объект с комплексом признаков К* относится к диагнозу (классу) с наибольшей вероятностью К* Di, если: P(Di/K*)> P(Dj/K*), j=1, 2, …l; ij. 2. САМОСТОЯТЕЛЬНЫЙ РАСЧЕТ ДИАГНОЗА ОПОРЫ ПО ВАРИАНТАМ ЗАДАНИЙ На основании исходных данных составим таблицу вероятных априорных признаков и состояний опоры (таблица 1). При этом появление признака Кj при диагнозе Di и не появление признака Кj при диагнозе Di будем считать полной группой событий. Тогда: Р(Кj/ Di) + Р(Кj/ Di) = 1. Таблица 1. Вероятные априорные признаки и состояния опоры Di Р(К1/ Di) Р(К1/ Di) Р(К2/ Di) Р(К2/ Di) Р(Di) D1 0,27 0,73 0,15 0,85 0,05 D2 0,41 0,59 0,25 0,75 0,04 D3 0,05 0,95 0,00 1 0,91 Определим вероятности диагнозов D1, D2 и D3 при наличии признаков К1 и К2: - вероятность наличия трещин в бетоне опоры (диагноз D1) при наличии признаков К1 и К2 составит: PD1K1K2=0,27*0,15*0,050,27*0,15*0,05+0,41*0,25*0,04+0,05*0*0,91=0,330 - вероятность наличия коррозии в арматуре опоры (диагноз D2) при наличии признаков К1 и К2 составит: P(D2/K1K2)=0,41*0,25*0,040,27*0,15*0,05+0,41*0,25*0,04+0,05*0*0,91=0,670 - вероятность исправного состояния опоры (диагноз D3) при наличии признаков К1 и К2 составит: P(D3/K1K2)=0,05*0*0,910,27*0,15*0,05+0,41*0,25*0,04+0,05*0*0,91=0,00 Определим вероятности диагнозов D1, D2 и D3 при отсутствии признака К1 и наличии признака К2: - вероятность наличия трещин в бетоне опоры (диагноз D1) при отсутствии признака К1 и наличии признака К2 составит: PD1K1K2=0,73*0,15*0,050,73*0,15*0,05+0,59*0,25*0,04+0,95*0*0,91=0,481 - вероятность наличия коррозии в арматуре опоры (диагноз D2) при отсутствии признака К1 и наличии признака К2 составит: PD2K1K2=0,59*0,25*0,040,73*0,15*0,05+0,59*0,25*0,04+0,95*0*0,91=0,519 - вероятность исправного состояния опоры (диагноз D3) при отсутствии признака К1 и наличии признака К2 составит: PD3K1K2=0,95*0*0,910,73*0,15*0,05+0,59*0,25*0,04+0,95*0*0,91=0,00 Определим вероятности диагнозов D1, D2 и D3 при наличии признака К1 и отсутствии признака К2: - вероятность наличия трещин в бетоне опоры (диагноз D1) при наличии признака К1 и отсутствии признака К2 составит: PD1K1K2=0,27*0,85*0,050,27*0,85*0,05+0,41*0,75*0,04+0,05*1*0,91=0,165 - вероятность наличия коррозии в арматуре опоры (диагноз D2) при наличии признака К1 и отсутствии признака К2 составит: PD2K1K2=0,41*0,75*0,040,27*0,85*0,05+0,41*0,75*0,04+0,05*1*0,91=0,177 - вероятность исправного состояния опоры (диагноз D3) при наличии признака К1 и отсутствии признака К2 составит: PD3K1K2=0,05*1*0,910,27*0,85*0,05+0,41*0,75*0,04+0,05*1*0,91=0,656 2. Найдём вероятности, когда обнаружены оба признака P(Di/K1K2). Считая признаки независимыми, применим формулу. P (Di / K1K2) =; Вероятность состояния D1 при наличии признаков К 1 и К 2: P (D1/ K1K2) =. Вероятность состояния D2 при наличии признаков К 1 и К 2: P (D2/ K1K2) =. Вероятность состояния D3 при наличии признаков К 1 и К 2: P (D2/ K1K2) = 0. Определим вероятности нахождения опоры в различном состоянии, если обследование показало, что потенциал в норме (признак К 1 отсутствует), но увеличен декремент колебаний (признак К 2 наблюдается). Используем ту же формулу: P (D1/K2) = P (D2/K2) = P (D3/K2) =. Вычислим вероятности состояний, когда признак К 1 наблюдается, а признак К 2 - отсутствует: P (D1/K1) = P (D2/K1) = P (D3/K1) =. Для случая, когда не наблюдаются оба признака: P (D1/ ) = P (D2/ ) = СПИСОК ЛИТЕРАТУРЫ 1. Надежность и диагностика систем электроснабжения железных дорог: Учебник для вузов ж/д транспорта/ А.В. Ефимов, А.Г. Галкин. – М.: УМК МПС России, 2000, с. 398 … 401. 2. Классификация технических состояний систем методом Байеса: Методические указания к выполнению и оформлению расчетных работ, выполняемых на практических занятиях студентами специальностей 140606 и 190401 дневной и заочной форы обучения / Составители Ю.В.Киселев, С.А. Привалов, В.Н. Водолазов. – Самара: СамГАПС, 2006. – 12 с. |
